湖北省2022届高三下学期数学4月调研（二模）试卷

试卷更新日期：2022-05-11 类型：高考模拟

进入出卷网下载

一、单选题

1. 设 $A = {x | x > 1} ， B = {x | x^{2} - 2 x - 3 < 0}$ ，则 $(∁_{R} A) ∩ B =$ （）

A、 ${x | x > - 1}$ B、 ${x | - 1 < x \leq 1}$ C、 ${x | - 1 < x < 1}$ D、 ${x | 1 < x < 3}$

查看试题解析
2. 若复数z的满足 $z (1 + 2 i) = - 3 + 4 i$ ( $i$ 是虚数单位)，则复数z的实部是（）

A、1 B、2 C、i D、 $- 2 i$

查看试题解析
3. 函数 $f (x) = c o s (ω x + φ) (ω > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示，则函数 $f (x)$ 的解析式是（）

A、 $f (x) = c o s (x + \frac{π}{6})$ B、 $f (x) = c o s (x - \frac{π}{6})$ C、 $f (x) = c o s (2 x + \frac{π}{6})$ D、 $f (x) = c o s (2 x - \frac{π}{6})$

查看试题解析
4. 已知平行四边形 $A B C D$ 中， $A B = 3 ， A D = 6 ， \vec{E C} = 2 \vec{D E} ， \vec{F C} = 2 \vec{B F}$ ，则 $\vec{E F} \cdot \vec{A C} =$ （）

A、9 B、-9 C、18 D、-18

查看试题解析
5. 已知 ${(2 x^{2} - \frac{1}{x})}^{n} (n \in N^{*})$ 的展开式中各项的二项式系数之和为64，则其展开式中 $x^{3}$ 的系数为（）

A、160 B、-160 C、60 D、-60

查看试题解析
6. 在四棱锥 $P - A B C D$ 中， $P A ⊥$ 平面 $A B C D ， A P = 2$ ，点M是矩形 $A B C D$ 内（含边界）的动点，且 $A B = 1 ， A D = 3$ ，直线 $P M$ 与平面 $A B C D$ 所成的角为 $\frac{π}{4}$ ．记点M的轨迹长度为 $α$ ，则 $t a n α =$ （）

A、 $\frac{\sqrt{3}}{3}$ B、1 C、 $\sqrt{3}$ D、2

查看试题解析
7. 已知 $F_{1}$ 、 $F_{2}$ 是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左，右焦点，过 $F_{1}$ 的直线l与双曲线C交于M，N两点，且 $\vec{F_{1} N} = 3 \vec{F_{1} M} ， | F_{2} M | = | F_{2} N |$ ，则C的离心率为（）

A、 $\sqrt{2}$ B、 $\sqrt{5}$ C、 $\sqrt{7}$ D、3

查看试题解析
8. 已知函数 $f (x) = l g (| x | - 1) + 2^{x} + 2^{- x}$ ，则使不等式 $f (x + 1) < f (2 x)$ 成立的x的取值范围是（）

A、 $(- \infty ， - 1) ∪ (1 ， + \infty)$ B、 $(- 2 ， - 1)$ C、 $(- \infty ， - \frac{1}{3}) ∪ (1 ， + \infty)$ D、 $(- \infty ， - 2) ∪ (1 ， + \infty)$

查看试题解析

二、多选题

9. 已知甲、乙两个水果店在“十一黄金周”七天的水果销售量统计如图所示，则下列说法正确的是（）

A、甲组数据的极差大于乙组数据的极差 B、若甲，乙两组数据的平均数分别为 $\bar{x_{1}} ， \bar{x_{2}}$ ，则 $\bar{x_{1}} > \bar{x_{2}}$ C、若甲，乙两组数据的方差分别为 $s_{1}^{2} ， s_{2}^{2}$ ，则 $s_{1}^{2} > s_{2}^{2}$ D、甲组数据的中位数大于乙组数据的中位数

查看试题解析
10. 定义空间两个非零向量的一种运算： $\vec{a} \otimes \vec{b} = | \vec{a} | | \vec{b} | \cdot s i n 〈 \vec{a} ， \vec{b} 〉$ ，则关于空间向量上述运算的以下结论中恒成立的有（）

A、 $E F G$ B、 $A B$ C、若 $\vec{a} \otimes \vec{b} = 0$ ，则 $\vec{a} ⊥ \vec{b}$ D、 $| \vec{a} \otimes \vec{b} | \leq | \vec{a} | | \vec{b} |$

查看试题解析
11. 设动直线 $l ： m x - y - 2 m + 3 = 0 (m \in R)$ 交圆 $C ： (x - 4)^{2} + (y - 5)^{2} = 12$ 于A，B两点（点C为圆心），则下列说法正确的有（）

A、直线l过定点 $(2 ， 3)$ B、当 $| A B |$ 取得最小值时， $m = 1$ C、当 $∠ A C B$ 最小时，其余弦值为 $\frac{1}{4}$ D、 $\vec{A B} \cdot \vec{A C}$ 的最大值为24

查看试题解析
12. 在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，已知 $E$ 为线段 $B_{1} C$ 的中点，点 $F$ 和点 $P$ 分别满足 $\vec{D_{1} F} = λ \vec{D_{1} C_{1}}$ ， $\vec{D_{1} P} = μ \vec{D_{1} B}$ ，其中 $λ$ ， $μ \in [0$ ， $1]$ ，则（）

A、当 $λ = \frac{1}{2}$ 时，三棱锥 $P - E F D$ 的体积为定值 B、当 $μ = \frac{1}{2}$ 时，四棱锥 $P - A B C D$ 的外接球的表面积是 $\frac{9 π}{4}$ C、若直线 $C P$ 与平面 $A B C D$ 所成角的正弦值为 $\frac{2}{3}$ ，则 $μ = \frac{1}{3}$ D、存在唯一的实数对 $(λ ， μ)$ ，使得 $D P ⊥$ 平面 $E F P$

查看试题解析

三、填空题

13. 若随机变量 $X ∼ N (3 ， σ^{2})$ ，且 $P (X > 5) = 0.2$ ，则 $P (1 \leq X \leq 5)$ 等于．

查看试题解析
14. 九连环是我国从古至今广泛流传的一种益智游戏，它用九个圆环相连成串，以解开为胜．用 $a_{n}$ 表示解下 $n (n \leq 9 ， n \in N^{*})$ 个圆环所需的最少移动次数．若 $a_{1} = 1$ ，且 $a_{n + 1} = {\begin{array}{l} 2 a_{n} + 2 ， n 为奇数， \\ 2 a_{n} - 1 ， n 为偶数， \end{array}$ 则解下6个圆环所需的最少移动次数为．

查看试题解析
15. 已知函数 $f (x) = x + l n (x - 1) ， g (x) = x l n x$ ，若 $f (x_{1}) = 1 + 2 l n t ， g (x_{2}) = t^{2}$ ，则 $\frac{l n t}{x_{1} x_{2} - x_{2}}$ 的最大值为．

查看试题解析
16. 设抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点为F，准线为l，过第一象限内的抛物线上一点A作l的垂线，垂足为B．设 $C (2 p ， 0) ， A F$ 与 $B C$ 相交于点D．若 $| C F | = | A F |$ ，且 $△ A C D$ 的面积为 $\frac{9}{2} \sqrt{2}$ ，则直线 $A C$ 的斜率 $k =$ ，抛物线的方程为．

查看试题解析

四、解答题

17. 如图，在平面四边形 $A B C D$ 中， $A B ⊥ A D ， A B = 1 ， A D = \sqrt{3} ， B C = \sqrt{2}$ ．

(1)、若 $C D = 2$ ，求 $s i n ∠ A D C$ ；

(2)、若 $∠ C = 45 °$ ，求四边形 $A B C D$ 的面积．

查看试题解析
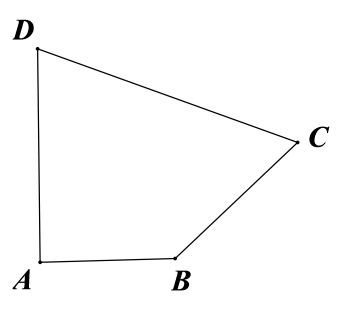18. 已知正项等差数列 ${a_{n}}$ 满足： $a_{3 n} = 3 a_{n} (n \in N^{*})$ ，且 $2 a_{1} ， a_{3} + 1 ， a_{8}$ 成等比数列．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $c_{n} = \frac{2^{a_{n + 1}}}{(1 + 2^{a_{n}}) (1 + 2^{a_{n + 1}})}$ ， $R_{n}$ 是数列 ${c_{n}}$ 的前n项和，若对任意 $n \in N^{*}$ 均有 $R_{n} < λ$ 恒成立，求 $λ$ 的最小值．

查看试题解析
19. 某企业使用新技术对某款芯片进行试生产，在试产初期，该款芯片的生产有四道工序，前三道工序的生产互不影响，第四道是检测评估工序，包括智能自动检测与人工抽检．已知该款芯片在生产中，前三道工序的次品率分别为 $P_{1} = \frac{1}{10} ， P_{2} = \frac{1}{9} ， P_{3} = \frac{1}{8}$ ．

(1)、求该款芯片生产在进人第四道工序前的次品率；

(2)、如果第四道工序中智能自动检测为次品的芯片会被自动淘汰，合格的芯片进入流水线并由工人进行人工抽查检验．在芯片智能自动检测显示合格率为90%的条件下，求工人在流水线进行人工抽检时，抽检一个芯片恰为合格品的概率．

查看试题解析
20. 如图在斜三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A A_{1} = A B = A C = B C = 12 ， ∠ A_{1} A C = 60 °$ ，侧面 $A C C_{1} A_{1} ⊥$ 底面 $A B C$ ，点M，N分别为 $A_{1} B ， B C$ 的中点，点D为线段 $A C$ 上一点，且 $A D = \frac{1}{3} A C$ ．

(1)、求证： $A M / /$ 平面 $A_{1} D N$ ；

(2)、求二面角 $M - A N - C$ 的正弦值．

查看试题解析
21. 在平面直角坐标系中 $x O y$ ，椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率为 $\frac{\sqrt{3}}{2}$ ，点 $(- \sqrt{3} ， \frac{1}{2})$ 在椭圆C上．

(1)、求椭圆C的方程；

(2)、设椭圆C的左、右顶点分别为A，B，点P，Q为椭圆上异于A，B的两动点，记直线 $A P$ 的斜率为 $k_{1}$ ，直线 $Q B$ 的斜率为 $k_{2}$ ，已知 $k_{1} = 7 k_{2}$ ．
①求证：直线 $P Q$ 恒过x轴上一定点；
②设 $△ P Q B$ 和 $△ P Q A$ 的面积分别为 $S_{1} ， S_{2}$ ，求 $| S_{1} - S_{2} |$ 的最大值．

查看试题解析
22. 已知函数 $f (x) = x e^{x} - 1 ， g (x) = a (l n x + x)$ ．

(1)、若不等式 $f (x) \geq g (x)$ 恒成立，求正实数a的值；

(2)、证明： $x^{2} e^{x} > (x + 2) l n x + 2 s i n x$ ．

查看试题解析