河南省新乡市2022届高三理数第三次模拟试卷
试卷更新日期:2022-05-11 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知复数z满足 , 则( )A、1 B、 C、 D、3. 设等比数列的公比为q,若 , 则( )A、2 B、3 C、4 D、54. 若函数的图象在点处的切线方程为 , 则( )A、1 B、-1 C、0 D、25. 已知一个圆柱与一个圆锥的轴截面分别为正方形与正三角形,且正方形与正三角形的边长相等,则该圆柱的体积与圆锥的体积的比值为( )A、 B、 C、 D、6. 已知双曲线的顶点到一条渐近线的距离为实轴长的 , 则双曲线C的离心率为( )A、 B、2 C、 D、37. 已知的展开式中各项的系数之和为2,则展开式中含项的系数为( )A、-20 B、-10 C、10 D、408. 为了贯彻落实中央新疆工作座谈会和全国对口支援新疆工作会议精神,促进新疆教育事业发展,某市教育系统选派了三位男教师和两位女教师支援新疆,这五位教师被分派到三个不同地方对口支援,每位教师只去一个地方,每个地方都有老师去,则两位女教师被分派到同一个地方的概率为( )A、 B、 C、 D、9. 中国的5G技术领先世界,5G技术的数学原理之一便是著名的香农公式:.它表示,在受噪音干扰的信道中,最大信息传递速度C取决于信道带宽W,信道内信号的平均功率S,信道内部的高斯噪声功率N的大小,其中叫作信噪比.当信噪比比较大时,公式中真数里面的1可以忽略不计.按照香农公式,增加带宽,提高信号功率和降低噪声功率都可以提升信息传递速度,若在信噪比为1000的基础上,将带宽W增大到原来的2倍,信号功率S增大到原来的10倍,噪声功率N减小到原来的 , 则信息传递速度C大约增加了( )(参考数据:)A、87% B、123% C、156% D、213%10. 已知抛物线的焦点为F,P点在抛物线上,Q点在圆上,则的最小值为( )A、4 B、6 C、8 D、1011. 如图所示的是一个简单几何体的三视图,若 , 则该几何体外接球体积的最小值为( )
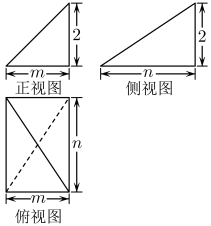 A、 B、 C、 D、12. 已知数列满足 , , 则数列的前2022项和为( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知数列满足 , , 则数列的前2022项和为( )A、 B、 C、 D、二、填空题
-
13. 设x,y满足约束条件则的最大值为.14. 已知 , , , 则在方向上的投影为.15. 已知函数 , 若对任意的恒成立,且在上单调递减,则.16. 黎曼函数是一个特殊的函数,由德国数学家波恩哈德·黎曼发现并提出,在高等数学中有着广泛的应用.黎曼函数定义在上,其解析式如下:若函数是定义在R上的奇函数,且对任意x都有 , 当时, , 则.
三、解答题
-
17. 在平面四边形中,已知 , , .
 (1)、若 , 求;(2)、若的面积为 , 求的面积.18. 为进一步完善公共出行方式,倡导“绿色出行”和“低碳生活”,某市建立了公共自行车服务系统,为了鼓励市民租用公共自行车出行,同时希望市民尽快还车,方便更多的市民使用,公共自行车按每次的租用时间进行收费,具体收费标准如下:①租用时间不超过1小时,免费;②租用时间超出1小时但不超过2小时,收费1元;③租用时间超出2小时,按每小时1元(不足1小时按1小时计算)收费,一天最高收费10元.甲、乙两人独立出行,每天都需要租用公共自行车一次,且两人租车时间都不会超过3小时,已知甲、乙租用时间不超过一小时的概率分别是 , ;租用时间超出1小时且不超过2小时的概率分别是 , ;租用时间超出2小时的概率分别是 , .(1)、求甲一天内租用公共自行车的费用比乙多的概率;(2)、设甲两天内租用公共自行车的总费用为X,求随机变量X的分布列和数学期望.19. 如图,在四棱锥中,底面ABCD是直角梯形, , , , , , 平面平面ABCD,且 , E为BC的中点.
(1)、若 , 求;(2)、若的面积为 , 求的面积.18. 为进一步完善公共出行方式,倡导“绿色出行”和“低碳生活”,某市建立了公共自行车服务系统,为了鼓励市民租用公共自行车出行,同时希望市民尽快还车,方便更多的市民使用,公共自行车按每次的租用时间进行收费,具体收费标准如下:①租用时间不超过1小时,免费;②租用时间超出1小时但不超过2小时,收费1元;③租用时间超出2小时,按每小时1元(不足1小时按1小时计算)收费,一天最高收费10元.甲、乙两人独立出行,每天都需要租用公共自行车一次,且两人租车时间都不会超过3小时,已知甲、乙租用时间不超过一小时的概率分别是 , ;租用时间超出1小时且不超过2小时的概率分别是 , ;租用时间超出2小时的概率分别是 , .(1)、求甲一天内租用公共自行车的费用比乙多的概率;(2)、设甲两天内租用公共自行车的总费用为X,求随机变量X的分布列和数学期望.19. 如图,在四棱锥中,底面ABCD是直角梯形, , , , , , 平面平面ABCD,且 , E为BC的中点. (1)、证明:平面平面PBD.(2)、若四棱锥的体积为 , 求二面角的余弦值.20. 已知椭圆的离心率 , 且椭圆C经过点.(1)、求椭圆C的方程.(2)、不过点P的直线与椭圆C交于A,B两点,记直线PA,PB的斜率分别为 , , 试判断是否为定值.若是,求出该定值;若不是,请说明理由.
(1)、证明:平面平面PBD.(2)、若四棱锥的体积为 , 求二面角的余弦值.20. 已知椭圆的离心率 , 且椭圆C经过点.(1)、求椭圆C的方程.(2)、不过点P的直线与椭圆C交于A,B两点,记直线PA,PB的斜率分别为 , , 试判断是否为定值.若是,求出该定值;若不是,请说明理由.