河北省唐山市2022届高三数学二模试卷
试卷更新日期:2022-05-11 类型:高考模拟
一、单选题
-
1. 设全集 , 集合 , , 则( )A、 B、 C、{2} D、2. 已知复数z满足 , 则( )A、 B、 C、 D、23. 将函数的图象向右平移个单位,可以得到( )A、的图象 B、的图象 C、的图象 D、的图象4. 如图,圆锥的轴为PO,其底面直径和高均为2,过PO的中点作平行底面的截面,以该截面为底面挖去一个圆柱,此圆柱的下底面在圆锥的底面上,则圆锥与所得圆柱的体积之比为( )
 A、 B、 C、 D、5. F为抛物线的焦点,点在C上,直线MF交C的准线于点N,则( )A、 B、 C、5 D、126. 已知实数x,y满足 , 则的最大值是( )A、 B、 C、6 D、37. 已知函数 , 若 , 则x的取值范围是( )A、 B、 C、 D、8. 已知 , 函数 , 若 , 则( )A、 B、 C、 D、
A、 B、 C、 D、5. F为抛物线的焦点,点在C上,直线MF交C的准线于点N,则( )A、 B、 C、5 D、126. 已知实数x,y满足 , 则的最大值是( )A、 B、 C、6 D、37. 已知函数 , 若 , 则x的取值范围是( )A、 B、 C、 D、8. 已知 , 函数 , 若 , 则( )A、 B、 C、 D、二、多选题
-
9. 已知的展开式中第3项与第8项的二项式系数相等,则( )A、n=9 B、 C、常数项是672 D、展开式中所有项的系数和是-110. 小李上班可以选择公交车、自行车两种交通工具,他分别记录了100次坐公交车和骑车所用时间(单位:分钟),得到下列两个频率分布直方图:

基于以上统计信息,则( )
A、骑车时间的中位数的估计值是22分钟 B、骑车时间的众数的估计值是21分钟 C、坐公交车时间的中位数的估计值是20分钟 D、坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值11. 双曲线具有如下光学性质:如图 , 是双曲线的左、右焦点,从右焦点发出的光线m交双曲线右支于点P,经双曲线反射后,反射光线n的反向延长线过左焦点 . 若双曲线C的方程为 , 下列结论正确的是( )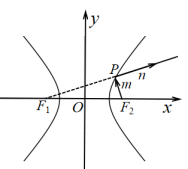 A、若 , 则 B、当n过时,光由所经过的路程为13 C、射线n所在直线的斜率为k,则 D、若 , 直线PT与C相切,则12. 如图,正方体中,顶点A在平面内,其余顶点在的同侧,顶点 , B,C到的距离分别为 , 1,2,则( )
A、若 , 则 B、当n过时,光由所经过的路程为13 C、射线n所在直线的斜率为k,则 D、若 , 直线PT与C相切,则12. 如图,正方体中,顶点A在平面内,其余顶点在的同侧,顶点 , B,C到的距离分别为 , 1,2,则( )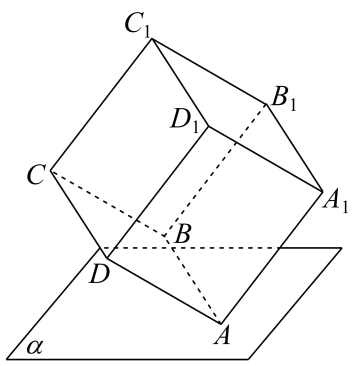 A、平面 B、平面平面 C、直线与所成角比直线与所成角大 D、正方体的棱长为
A、平面 B、平面平面 C、直线与所成角比直线与所成角大 D、正方体的棱长为三、填空题
-
13. 设向量 , , 若与共线,则实数 .14. 若圆的圆心在直线上,则C的半径为 .15. 已知数列满足 , , 则前5项和的最大值为 .16. 若函数 , , 则的最小值为;若 , 且 , 则的最小值为 .
四、解答题
-
17. 已知等比数列满足 , , .(1)、求的通项公式;(2)、记 , , 求数列的前n项和 .18. 的内角A,B,C的对边分别为a,b,c,已知 , .(1)、求A;(2)、若点D在BC边上,AD平分BAC,且 , 求的周长.19. 如图,是边长为的等边三角形,E,F分别为AB,AC的中点,G是的中心,以EF为折痕把折起,使点A到达点P的位置,且平面ABC.
 (1)、证明:;(2)、求平面PEF与平面PBF所成二面角的正弦值.20. 目前,全国多数省份已经开始了新高考改革.改革后,考生的高考总成绩由语文、数学、外语3门全国统一考试科目成绩和3门选择性科目成绩组成.注:甲、乙两名同学对选择性科目的选择是随机的.(1)、A省规定:选择性考试科目学生可以从思想政治、历史、地理、物理、化学、生物6门科目中任选3门参加选择性考试.求甲同学在选择物理科目的条件下,选择化学科目的概率;(2)、B省规定:3门选择性科目由学生首先从物理科目和历史科目中任选1门,再从思想政治、地理、化学、生物4门科目中任选2门.
(1)、证明:;(2)、求平面PEF与平面PBF所成二面角的正弦值.20. 目前,全国多数省份已经开始了新高考改革.改革后,考生的高考总成绩由语文、数学、外语3门全国统一考试科目成绩和3门选择性科目成绩组成.注:甲、乙两名同学对选择性科目的选择是随机的.(1)、A省规定:选择性考试科目学生可以从思想政治、历史、地理、物理、化学、生物6门科目中任选3门参加选择性考试.求甲同学在选择物理科目的条件下,选择化学科目的概率;(2)、B省规定:3门选择性科目由学生首先从物理科目和历史科目中任选1门,再从思想政治、地理、化学、生物4门科目中任选2门.①求乙同学同时选择物理科目和化学科目的概率;
②为调查学生的选科情况,从某校高二年级抽取了10名同学,其中有6名首选物理,4名首选历史.现从这10名同学中再选3名同学做进一步调查.将其中首选历史的人数记作X,求随机变量X的分布列和数学期望.
