贵州省遵义市2022届高三理数第三次统一考试试卷

试卷更新日期：2022-05-11 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {0 ， 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7}$ ， $B = {1 ， 2 ， 4 ， 6}$ ，则 $A ∩ B =$ （）

A、 ${2 ， 4}$ B、 ${1 ， 2 ， 4}$ C、 ${1 ， 2 ， 4 ， 6}$ D、 ${2 ， 4 ， 6}$

查看试题解析
2. 若 $x < 0$ ，则 $x + \frac{1}{x}$ 的最大值为（）

A、-2 B、 $- 2 \sqrt{2}$ C、 $- \frac{3}{2}$ D、2

查看试题解析
3. 若复数z满足 $| 1 - i | z = 2$ （i为虚数单位），则复数z在复平面内所对应的点在（）

A、第一象限 B、实轴上 C、第三象限 D、虚轴上

查看试题解析
4. 命题“ $\forall x > 0 ， l n x - x + 1 \leq 0$ ”的否定是（）

A、“ $\forall x \leq 0 ， l n x - x + 1 \leq 0$ ” B、“ $\exists x \leq 0 ， l n x - x + 1 > 0$ ” C、“ $\exists x > 0 ， l n x - x + 1 \leq 0$ ” D、“ $\exists x > 0 ， l n x - x + 1 > 0$ ”

查看试题解析
5. 贵州等七省份宣布从2021年秋季入学高一新生开始进入“ $3 + 1 + 2$ ”的新高考模式，2024年起高考不分文理新高考“ $3 + 1 + 2$ ”模式指的是，“3”即语文、数学、外语3门统一高考科目；“1”和“2”为选择性考试科目，其中“1”是从物理或历史科目中选择1门；“2”是从思想政治、地理、化学、生物学中选择2门．则新高考模式的不同组合有（）

A、12种 B、10种 C、9种 D、8种

查看试题解析
6. 已知 $\vec{a}$ 和 $\vec{b}$ 为非零向量，且 $| 2 \vec{a} + 3 \vec{b} | = | 2 \vec{a} - 3 \vec{b} |$ ， $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{2}$ D、 $\frac{2 π}{3}$

查看试题解析
7. 已知二项式 ${(x - \frac{1}{\sqrt{x}})}^{n}$ 展开式的二项式系数和为64，则展开式中常数项为（）

A、10 B、15 C、18 D、30

查看试题解析
8. 将函数 $y = f (x)$ 图像上的所有点的横坐标伸长到原来的2倍，纵坐标不变，再把所得曲线向左平移 $\frac{π}{6}$ 个单位长度，得到曲线 $y = c o s (x + \frac{π}{3})$ ，则 $f (x)$ 的解析式为（）

A、 $y = c o s (2 x + \frac{π}{6})$ B、 $y = c o s (\frac{1}{2} x + \frac{π}{6})$ C、 $y = c o s (\frac{1}{2} x - \frac{π}{6})$ D、 $y = c o s (2 x + \frac{π}{3})$

查看试题解析
9. 如图，边长为2的等边三角形，取其中线的 $\frac{2}{3}$ ，构成新的等边三角形，面积为 $S_{1}$ ；再取新的等边三角形中线的 $\frac{2}{3}$ ，构成等边三角形，面积为 $S_{2}$ ；……如此下去，形成一个不断缩小的正三角形系列，则第5次构成的等边三角形的面积 $S_{5}$ ，为（）

A、 $\frac{\sqrt{3}}{81}$ B、 $\frac{16}{81} \sqrt{3}$ C、 $\frac{\sqrt{3}}{243}$ D、 $\frac{\sqrt{3}}{162}$

查看试题解析
10. $△ A B C$ 内角A，B，C的对边分别为a，b，c， $c = 2 ， t a n A + t a n B + \sqrt{3} = t a n A t a n B t a n C$ ，则 $△ A B C$ 周长的最大值为（）

A、4 B、6 C、8 D、10

查看试题解析
11. 满足不等式 $(x - 1^{2}) (x - 2^{2}) (x - 3^{2}) ⋯ (x - 10 0^{2}) \leq 0$ 整数解个数为（）

A、4950 B、5000 C、5050 D、5100

查看试题解析
12. 已知 $a = s i n 2 ， b = l n 2 ， c = 2^{- \frac{1}{3}}$ ，则a，b，c的大小关系是（）

A、 $c < b < a$ B、 $a < b < c$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析

二、填空题

13. 已知函数 $f (x) = l n x + x$ ，则 $f (x)$ 在 $x = 1$ 处切线斜率为．

查看试题解析
14. 圆 $O ： x^{2} + y^{2} = 2$ 上点P到直线 $l ： 3 x + 4 y = 10$ 距离的最小值为．

查看试题解析
15. 若 $\sqrt{2} c o s 2 θ + s i n (θ + \frac{π}{4}) = 0 ， θ \in (0 ， \frac{π}{2})$ ，则 $c o s θ =$ ．

查看试题解析
16. 斜率为 $\frac{1}{2}$ 的直线 $l$ 过椭圆 $C ： \frac{y^{2}}{a^{2}} + \frac{x^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦点 $F$ ，交椭圆于 $A ， B$ 两点，若 $\vec{A F} = \frac{2}{3} \vec{A B}$ ，则该椭圆的离心率为．

查看试题解析

三、解答题

17. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前n项和， $S_{11} = 0 ， a_{7} = 2$ ．

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求 $\sum_{k = 1}^{100} | a_{k} |$ 的值．

查看试题解析
18. 如图，在直三棱柱 $A B C - A^{'} B^{'} C^{'}$ 中， $∠ A C B = 12 0^{∘}$ ， $A C = B C = 2$ ， $A B = B B^{'}$ ，点 $E ， F ， M$ 分别为 $B B^{'} ， A^{'} B^{'} ， C C^{'}$ 的中点．

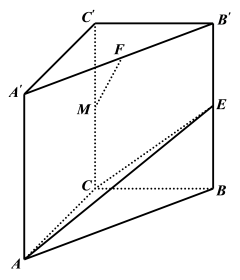(1)、判断 $M F$ 与平面 $A C E$ 的位置关系，并说明理由；

(2)、求二面角 $E - A C - B$ 的正弦值．

查看试题解析
19. 已知函数 $f (x) = l n x - a x + 1$ ，其中 $a \in R$ ．

(1)、讨论函数 $f (x)$ 的单调性；

(2)、若 $f (x) = 2 x$ 有且仅有两个不相等实根，求实数a的取值范围．

查看试题解析
20. 已知 $F_{1} ， F_{2}$ 为双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 左右焦点， $| F_{1} F_{2} | = 2 \sqrt{7}$ ，且该双曲线一条渐近线的斜率为 $\frac{\sqrt{3}}{2}$ ，点M和N是双曲线上关于x轴对称的两个点， $A_{1} ， A_{2}$ 为双曲线左右顶点．

(1)、求该双曲线的标准方程；

(2)、设 $N A_{1}$ 和 $M A_{2}$ 交点为P，则 $△ P F_{1} F_{2}$ 的面积是否存在最大值？若存在，请求出这个最大值；若不存在，请说明理由．

查看试题解析

21. 某中学在2021年高考分数公布后对高三年级各班的成绩进行分析．经统计，某班有50名同学，总分都在区间

[600 ， 700]

内，将得分区间平均分成5组，统计频数、频率后，得到了如图所示的“频率分布”折线图．

(1)、请根据频率分布折线图，画出频率分布直方图，并根据频率分布直方图估计该班级的平均分；

(2)、经相关部门统计，高考分数

\geq 680

以上的考生获得高校T“强基计划”入围资格，并制作高校T录取政策和考生录取预测统计表（如表所示）．第一轮笔试有2科，学生通过考试获得相应等级的事件相互独立且概率相同.

高考分数		$[680 ， 690]$				$> 690$
第一轮笔试	学科测试等级	$A^{+}$	A	B	C	$A^{+}$	A	B	C
第一轮笔试	学生通过考试获得相应等级概率	$\frac{1}{3}$	$\frac{1}{4}$	$\frac{1}{6}$	$\frac{1}{4}$	$\frac{2}{3}$	$\frac{1}{6}$	$\frac{1}{12}$	$\frac{1}{12}$
第二轮面试	入围条件	至少有1科 $A^{+}$ ，且2科均不低于B
录取条件	全 $A^{+}$	在第一轮笔试中2科均获得 $A^{+}$
录取条件	通过第二轮面试	考生通过概率为 $\frac{2}{5}$				考生通过概率为 $\frac{2}{3}$

若该班级考分前10名都已经报考了高校T的“强基计划”，且恰有2人成绩高于690分．求：

①总分高于690分的某位同学没有进入第二轮的概率 $P_{1}$ ；

②该班恰有两名同学通过“强基计划”被高校T录取的概率 $P_{2}$ ．

查看试题解析

22. 在极点为O的极坐标系中，经过点 $M (2 ， \frac{π}{6})$ 的直线l与极轴所成角为 $α$ ，且与极轴的交点为N．

(1)、当 $α = \frac{π}{2}$ 时，求l的极坐标方程；

(2)、当 $α \in [\frac{π}{4} ， \frac{π}{3}]$ 时，求 $△ M O N$ 面积的取值范围．

查看试题解析
23. 已知 $f (x) = | a x + 1 | - | x - 2 | ， a \in R$ ．

(1)、当 $a = 1$ 时，求 $f (x)$ 最大值；

(2)、当 $0 \leq a \leq 1$ 时，证明： $f (x) \geq 1$ 的解集非空．

查看试题解析