福建省宁德市普通高中2022届高三数学五月份质量检测试卷

试卷更新日期：2022-05-11 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $M = {x | x^{2} - 2 x - 8 < 0} ， N = {y | y \geq - 1]$ ，则 $M ∩ N$ =（）

A、[-1，4) B、[-1，2) C、(-2，-1) D、∅

查看试题解析
2. 若 $| z \cdot (1 + i) | = \sqrt{6}$ ，则 $z · \bar{z}$ 的值为（）

A、 $\sqrt{2}$ B、2 C、 $\sqrt{3}$ D、3

查看试题解析
3. 函数 $y = f (x)$ 的图象如图所示，则f（x）的解析式可能是（）

A、 $f (x) = 2 - 2^{x}$ B、 $f (x) = l o g_{2} (x + 2)$ C、 $f (x) = \sqrt{x + 2}$ D、 $f (x) = 1 - {(x - 2)}^{2}$

查看试题解析
4. 函数 $f (x) = s i n (ω x + \frac{π}{6}) (ω > 0)$ 的周期为2，下列说法正确的是（）

A、 $ω = \frac{π}{2}$ B、 $f (x + \frac{1}{3})$ 是奇函数 C、f（x）在[ $\frac{4}{3}$ ， $\frac{7}{3}$ ]上单调递增 D、 $y = f (x)$ 的图像关于直线 $x = - \frac{1}{3}$ 对称

查看试题解析
5. 已知点E是△ABC的中线BD上的一点（不包括端点）.若 $\vec{A E} = x \vec{A B} + y \vec{A C}$ ，则 $\frac{2}{x} + \frac{1}{y}$ 的最小值为（）

A、4 B、6 C、8 D、9

查看试题解析
6. 从0，1，2，…，9这十个数字中随机抽取3个不同的数字，记A为事件：“恰好抽的是2，4，6”，记B为事件：“恰好抽取的是6，7，8”，记C为事件：“抽取的数字里含有6”.则下列说法正确的是（）

A、 $P (A B) = P (A) P (B)$ B、 $P (C) = \frac{1}{10}$ C、 $P (C) = P (A B)$ D、 $P (A | C) = P (B | C ）$

查看试题解析
7. 贾宪是我国北宋著名的数学家，其创制的数字图式（如右图）又称“贾宪三角”，后被南宋数学家杨辉的著作《详解九章算法》所引用.n维空间中的几何元素与之有巧妙的联系，使我们从现实空间进入了虚拟空间.例如，1维最简几何图形线段它有2个0维的端点，1个1维的线段：2维最简几何图形三角形它有3个0维的端点，3个1维的线段，1个2维的三角形区域：…如下表所示.利用贾宪三角，从1维到9维最简几何图形中，所有1维线段数的和为（）
元素维度
几何体维度
0
1
2
3
n=1（线段）
2
1
n=2（三角形）
3
3
1
n=3（四面体）
4
6
4
1

……
……
……
……

A、120 B、165 C、215 D、240

查看试题解析
8. 若 $b \geq l n 2 x - a x$ 对 $x \in (0 ， + ∞)$ 恒成立，则 $\frac{b + 1}{a}$ 的最小值为（）

A、 $- \frac{1}{2 e}$ B、 $- \frac{1}{e}$ C、-1 D、0

查看试题解析

二、多选题

9. 某单位为了更好地开展党史学习教育，举办了一次党史知识测试，其200名职工成绩的频率分布直方图如图所示，则下列说法正确的是（）

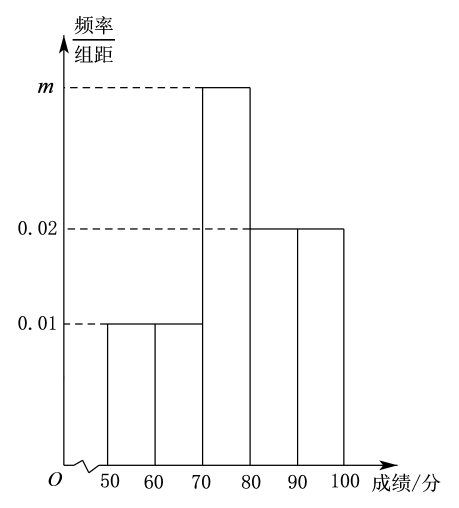A、图中的 $m = 0.04$ B、成绩不低于80分的职工约80人 C、200名职工的平均成绩是80分 D、若单位要表扬成绩由高到低前25%职工，则成绩87分的职工A肯定能受到表扬

查看试题解析
10. 数列{ $a_{n}$ }中，设 $T_{n} = a_{1} \cdot a_{2} … … a_{n}$ .若 $T_{n}$ 存在最大值，则 $a_{n}$ 可以是（）

A、 $a_{n} = 2^{n - 6}$ B、 $a_{n} = {(- 1)}^{n}$ C、 $a_{n} = 2 n - 9$ D、 $a_{n} = \frac{n + 1}{2 n - 1}$

查看试题解析
11. 已知正方体ABCD-A₁B₁C₁D₁的棱长为2，F是正方形 $C D D_{1} C_{1}$ 的中心，则（）

A、三棱锥F- $B_{1} C C_{1}$ 的外接球表面积为4π B、 $B_{1} F / /$ 平面 $A_{1} B D$ C、 $C_{1} F ⊥$ 平面 $A_{1} C F$ ，且 $C_{1} F = \sqrt{2}$ D、若点E为BC中点，则三棱锥 $A_{1} - A B_{1} E$ 的体积是三棱锥 $A - F A_{1} B$ 体积的一半.

查看试题解析
12. 已知椭圆C： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ ，焦点 $F_{1}$ （-c，0）， $F_{2} (c ， 0) (c > 0)$ ，下顶点为B．过点 $F_{1}$ 的直线l与曲线C在第四象限交于点M，且与圆 $A ： {(x + 2 c)}^{2} + y^{2} = \frac{1}{4} c^{2}$ 相切，若 $\vec{M F_{2}} \cdot \vec{F_{1} F_{2}} = 0$ ，则下列结论正确的是（）

A、椭圆C上不存在点Q，使得 $Q F_{1} ⊥ Q F_{2}$ B、圆A与椭圆C没有公共点 C、当 $a = 3$ 时，椭圆的短轴长为2 $\sqrt{6}$ D、 $F_{2} B ⊥ F_{1} M$

查看试题解析

三、填空题

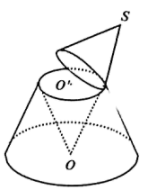
13. 若过点 $(\sqrt{2} ， 2)$ 的双曲线的渐近线为 $y = \pm 2 x$ ，则该双曲线的标准方程是.

查看试题解析
14. 在平面直角坐标系xOy中，圆O与x轴的正半轴交于点A，点B，C在圆O上，若射线OB平分∠AOC，B（ $\frac{3}{5}$ ， $\frac{4}{5}$ ），则点C的横坐标为.

查看试题解析
15. 已知 $f (x)$ 是定义在R上的偶函数，当 $x \geq 0$ 时， $f (x) = (x - 2 a) e^{x} + 2 a^{2} - 4$ .若 $f (x)$ 的图象与x轴恰有三个交点，则实数a的值为.

查看试题解析
16. 如图为某企业的产品包装盒的设计图，其设计方案为：将圆锥SO截去一小圆锥 $S O^{'}$ 作包装盒的盖子，再将剩下的圆台挖去以O为顶点，以圆 $O^{'}$ 为底面的圆锥 $O O^{'}$ .若圆O半径为3， $S O = 3 \sqrt{3}$ ，不计损耗，当圆锥 $O O^{'}$ 的体积最大时，圆 $O^{'}$ 的半径为，此时，去掉盖子的几何体的表面积为.

查看试题解析

四、解答题

17. 已知△ABC的内角A，B，C所对的边分别是a，b，c，且 $c c o s (A - \frac{π}{6}) = a s i n C$

(1)、求A；

(2)、若 $a = \sqrt{7} ， c = 1$ ， D是BC上的点，AD平分 $∠ B A C$ ，求AD的长

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $C D = 2 ， P D = A D = 1 ， P C = \sqrt{5}$ ，点 $E$ 为线段 $P C$ 上的点，且 $B C ⊥ D E$

(1)、证明： $P D ⊥ A C$ ；

(2)、若二面角 $E - A D - B$ 的大小为 $\frac{π}{4}$ ，求直线 $B P$ 与平面 $E A D$ 所成的角.

查看试题解析
19. 设数列{ $a_{n}$ }的前n项和为 $S_{n}$ ， $a_{1} = 3$ .数列 ${S_{n} + 3}$ 为等比数列，且 $S_{1} ， S_{3} ， S_{4} - 2 S_{1}$ 成等差数列.

(1)、求数列{ $S_{n}$ }的通项公式；

(2)、若 $N < \frac{{(- 1)}^{n} \cdot S_{n}}{a_{n}} < M$ ，求 $M - N$ 的最小值.

查看试题解析
20. 某地为调查国家提出的乡村振兴战略目标实施情况，随机抽查了100件某乡村企业生产的产品，经检验，其中一等品80件，二等品15件，次品5件，若销售一件产品，一等品利润为30元，二等品利润为20元，次品直接销毁，亏损40元.
附：对于一组数据 $(u_{i} ， v_{i}) (i = 1 ， 2 ， 3 ， ⋯ ， n)$ ，其回归直线 $\hat{v} = \hat{b} u + \hat{a}$ 的斜率和截距的最小二乘估计分别为 $\hat{b} = \frac{\sum_{i = 1} u_{i} v_{i} - n \bar{u} \bar{v}}{\sum_{i = 1} {u_{i}}^{2} - n {\bar{u}}^{2}} ， \hat{a} = \bar{v} - \hat{b} \bar{u}$

(1)、用频率估计概率，求从中随机抽取一件产品的利润的期望值.

(2)、根据统计，由该乡村企业的产量y（万只）与月份编号x（记年份2021年10月，2021年11月，…分别为 $x = 1 ， x = 2$ ， …，依此类推）的散点图，得到如下判断：产量y（万只）与月份编号x可近似满足关系式 $y = c \cdot x^{b}$ （c，b为大于0的常数），相关统计量的值如下表所示：
$\sum_{i = 1}^{6} (l n x_{i} \cdot l n y_{i})$
$\sum_{i = 1} (l n x_{i})$
$\sum_{i = 1}^{6} (l n y_{i})$
$\sum_{i = 1}^{6} (l n x_{i})^{2}$
-1.87
6.60
-2.70
9.46
根据所给统计量，求y关于x的回归方程；并估计该企业今年6月份的利润为多少万元（估算取 $e \approx 2.7$ ，精确到0.1）？

查看试题解析
21. 已知抛物线C： $y^{2} = 2 p x (p > 0)$ 上的一点M（ $x_{0}$ ， 4）到C的焦点F的距离为5.

(1)、求p的值；

(2)、若 $x_{0} > 1$ ，点A，B在抛物线C上，且 $M A ⊥ M B ， M N ⊥ A B$ ， N为垂足，当|MN|最大时，求直线AB的方程.

查看试题解析
22. 已知函数 $f (x) = e^{x} s i n x + a x$

(1)、若 $a = 1$ ，判断f（x）在（ $- \frac{π}{2}$ ， 0）的单调性；

(2)、从下面两个条件中选一个，求a的取值范围.
①f（x）在[0， $\frac{π}{2}$ ]上有且只有2个零点；
②当 $x \in [0 ， \frac{π}{2}]$ 时， $f (x) \geq x^{2}$ .

查看试题解析

元素维度几何体维度	0	1	2	3
n=1（线段）	2	1
n=2（三角形）	3	3	1
n=3（四面体）	4	6	4	1
		……	……	……	……

$\sum_{i = 1}^{6} (l n x_{i} \cdot l n y_{i})$	$\sum_{i = 1} (l n x_{i})$	$\sum_{i = 1}^{6} (l n y_{i})$	$\sum_{i = 1}^{6} (l n x_{i})^{2}$
-1.87	6.60	-2.70	9.46