青海省2022年中考一模数学试题

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上的点M表示的实数可能是（）

A、3.5 B、-2.5 C、-3.4 D、3.4

查看试题解析
2. 已知点P在第二象限，且到x轴的距离为2，到y轴的距离是3，则点P的坐标为（）

A、 $(- 3 ， 2)$ B、 $(3 ， - 2)$ C、 $(- 2 ， 3)$ D、 $(2 ， - 3)$

查看试题解析
3. 已知三角形两边的长分别是3cm和6cm，则该三角形的第三边的长可能是（）

A、2cm B、3cm C、5cm D、9cm

查看试题解析
4. 如图是由五个大小相同的正方体搭成的几何体，则关于它的视图，下列说法正确的是（）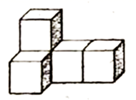

A、主视图的面积最小 B、左视图的面积最小 C、俯视图的面积最小 D、主视图，俯视图，左视图的面积一样大

查看试题解析
5. 反比例函数 $y = \frac{k}{x}$ 与直线 $y = - 2 x$ 相交于点A，A点的横坐标为－1，则此反比例函数的解析式为（）

A、 $y = \frac{2}{x}$ B、 $y = \frac{1}{2 x}$ C、 $y = - \frac{2}{x}$ D、 $y = - \frac{1}{2 x}$

查看试题解析
6.
如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上的一个动点，若PA=2，则PQ的最小值为（）

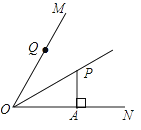A、1 B、2 C、3 D、4

查看试题解析
7. 如图，扇形OAB的半径为6cm，AC切 $\overset{⌢}{A B}$ 于点A交OB的延长线于点C．如果 $\overset{⌢}{A B}$ 的长为3cm， $A C = 4$ cm，则图中阴影部分的面积为（）

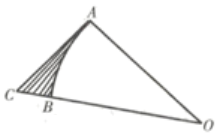A、1 cm² B、6 cm² C、4 cm² D、3 cm²

查看试题解析
8. 如图，在 $△ A B C$ 中， $A C = A B ，$ 有一动点P从点B出发，沿 $B \to A \to C \to B$ 匀速运动．则 $A P$ 的长度S与时间t之间的函数关系用图象描述大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 当 $y =$ 时，代数式 $3 y + 7$ 与 $2 y - 5$ 的值互为相反数．

查看试题解析
10. 函数 $y = {(x - 2)}^{0} + \sqrt{x - 1}$ 的自变量x的取值范围是．

查看试题解析
11. 据国家能源局报道，截止2021年4月底，我国海上风电并网容量达1042万千瓦，将数据“1042万”用科学记数法表示为．

查看试题解析
12. 关于x的方程mx²+mx+1=0有两个相等的实数根，那么m=.

查看试题解析
13. 把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16厘米，则球的半径为厘米．

查看试题解析
14. 如图，等边△ABC的边长为2cm，D，E分别是AB，AC上的点，将△ADE沿直线DE折叠，点A落在点 $A^{'}$ 处，且点 $A^{'}$ 在△ABC外部，则阴影部分图形的周长为 cm

查看试题解析
15. 将一副三角板按如图所示的方式摆放在一起，则∠1的度数是。

查看试题解析
16. 如图，将△OAB绕点O按逆时针方向旋转至 $△ O A^{'} B^{'}$ ，使点B恰好落在边 $A^{'} B^{'}$ 上，已知 $A B = 4$ cm， $B B^{^{'}} = 1$ cm，则 $A^{'} B$ 的长是．

查看试题解析
17. 如图，DE为△ABC的中位线，点F在DE上，且∠AFB＝90°，若AB＝5，BC＝8，则EF的长为．

查看试题解析
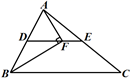18. 教师节来临之际，同学们给每位辛勤工作的老师准备了一束鲜花．同一种鲜花每枝的价格相同，从如图所示的信息可知第三束鲜花共计元．

查看试题解析
19. 已知一个等腰三角形一腰上的高与另一腰所成的夹角为42°，则顶角的度数为．

查看试题解析
20. 观察下列等式：
① $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} = 1 + \frac{1}{1} - \frac{1}{1 + 1} = 1 \frac{1}{2}$ ；② $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{2 + 1} = 1 \frac{1}{6}$ ；③ $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{3 + 1} = 1 \frac{1}{12}$ ；…根据以上规律，请写出第⑥个等式．

查看试题解析

三、解答题

21. 先化简 $(1 + \frac{3}{a - 2}) \div \frac{a^{2} - 1}{a^{2} - 4}$ ，然后给a选择一个你喜欢的值，代入求此式的值．

查看试题解析
22. 如图所示，已知Rt△ABC中， $∠ A C B = 90 °$ ．

(1)、尺规作图（请用2B铅笔）：作 $∠ B A C$ 的平分线AM交BC于D点（保留作图痕迹，不写作法）．

(2)、在（1）所作图形中，将Rt△ABC沿某条直线折叠，使点A与点D重合，折痕EF交AC于点E，交AB于点F，连接DE，DF．再展回到原图形，得到四边形AEDF，试判断四边形AEDF的形状并证明．

查看试题解析
23. 郑州市某中学体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶．已知看台高为1.6米，现要做一个不锈钢的扶手 $A B$ 及两根与 $F G$ 垂直且长为1米的不锈钢架杆 $A D$ 和 $B C$ (杆子的底端分别为 $D ， C$ )，且 $∠ D A B ＝ 66.5 °$ ，求所用不锈钢材料的总长度．(即 $A D + A B + B C$ ，结果精确到0.1米)参考数据( $s i n 66.5 ° \approx 0.92 ， c o s 66.5 ° \approx 0.40 ， t a n 66.5 ° \approx 2.30$ )

查看试题解析
24. 如图，已知 $⊙ O$ 是以AB为直径的圆，C为 $⊙ O$ 上一点，D为OC延长线上一点，BC的延长线交AD于E， $∠ D A C = ∠ D C E$ ．

(1)、求证：直线AD为 $⊙ O$ 的切线；

(2)、求证： $D C^{2} = E D \cdot D A$ ．

查看试题解析
25. 甲、乙两校参加县教育局举办的学生英语口语竞赛，两校参赛人数相等．比赛结束后，发现学生成绩分别为7分、8分、9分、10分（满分10分）．依据统计数据绘制了如下尚不完整的统计表1、扇形统计图1和条形统计图2．
表1甲校成绩统计表
分数
7分
8分
9分
10分
人数
11
0
…….
8

(1)、请你将统计图表中不完整的部分补充完整．

(2)、经计算，乙校的平均分是8.3分，中位数是8分．请写出甲校的平均分、中位数，并从平均分和中位数的角度分析哪个学校成绩较好．

(3)、如果该县教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手．请你分析，应选哪所学校？

(4)、该县教育局决定从乙校得10分的两男三女5人中，选取2人参加口语竞赛，请你用列表或画树状图的方法，求出恰好选取一男一女参赛的概率．

查看试题解析
26. 问题背景：在正方形ABCD的外侧，作△ADE和△DCF，连接AF，BE．

(1)、特例探究：如图1，若△ADE和△DCF均为等边三角形，试判断线段AF与BE的数量关系和位置关系，并说明理由；

(2)、拓展应用：如图2，在△ADE和△DCF中， $A E = D F$ ， $E D = F C$ ，且 $B E = 4$ ，求四边形ABFE的面积？

查看试题解析
27. 如图1（注：与图2完全相同）所示，直线 $y = x + c$ 与x轴交于点 $A (- 4 ， 0)$ ，与y轴交于点C，抛物线 $y = - x^{2} + b x + c$ 经过点A，C．点M是线段OA上的一动点，过点M且垂直于x轴的直线与直线AC和抛物线分别交于点P，N．

(1)、求抛物线的解析式；

(2)、当以C，P，N为顶点的三角形是直角三角形时，求△CPN的面积（请在图1中探求）；

(3)、过点N作 $N H ⊥ A C$ 于点H，求 $S_{△ H P N}$ 的最大值（请在图2中探求）．

查看试题解析

分数	7分	8分	9分	10分
人数	11	0	…….	8