辽宁省抚顺市东洲区2022年九年级模拟检测(二)数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 下列函数中,y是x的反比例函数的是( )A、 B、 C、 D、2. 如图,将一个长方体内部挖去一个圆柱,这个几何体的主视图是( )
 A、
A、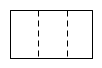 B、
B、 C、
C、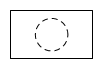 D、
D、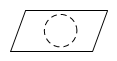 3. 观察下列图形,这四组形状各异的图形中,是相似图形的有( )
3. 观察下列图形,这四组形状各异的图形中,是相似图形的有( )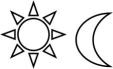



 A、1组 B、2组 C、3组 D、4组4. 已知反比例函数的图象如图所示,则实数m的取值范围是( )
A、1组 B、2组 C、3组 D、4组4. 已知反比例函数的图象如图所示,则实数m的取值范围是( )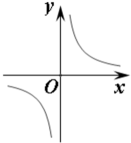 A、 B、 C、 D、5. 如图,为方便行人,打算修建一座高5 m的过街天桥,若天桥的斜面的坡度为 , 则斜坡的长度为( )
A、 B、 C、 D、5. 如图,为方便行人,打算修建一座高5 m的过街天桥,若天桥的斜面的坡度为 , 则斜坡的长度为( ) A、m B、m C、5m D、10m6. 如图是王老师展示的他昨天画的一幅写生画,他让四个学生猜测他画这幅画的时间.根据王老师标出的方向,下列给出的时间比较接近的是( )
A、m B、m C、5m D、10m6. 如图是王老师展示的他昨天画的一幅写生画,他让四个学生猜测他画这幅画的时间.根据王老师标出的方向,下列给出的时间比较接近的是( )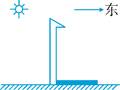 A、小丽说:“早上8点” B、小强说:“中午12点” C、小刚说:“下午3点” D、小明说:“哪个时间段都行”7. 一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )A、
A、小丽说:“早上8点” B、小强说:“中午12点” C、小刚说:“下午3点” D、小明说:“哪个时间段都行”7. 一个矩形木框在太阳光的照射下,在地面上的投影不可能是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,D是的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是( )
8. 如图,D是的边BC上的一点,那么下列四个条件中,不能够判定△ABC与△DBA相似的是( ) A、 B、 C、 D、9. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为( )
A、 B、 C、 D、9. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值为( )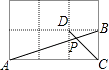 A、1 B、2 C、3 D、10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )
A、1 B、2 C、3 D、10. 如图,边长为1的正方形ABCD中,点E在CB的延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是( )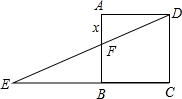 A、
A、 B、
B、 C、
C、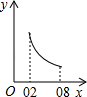 D、
D、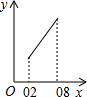
二、填空题
-
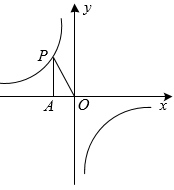
11. 在Rt△ABC中,∠C=90°,tanA= , 则cosA= .12. 如图,点P为反比例函数y=-图象上一点,过点P作 PA⊥x轴于点A,连接OP,则△PAO的面积为 .
 13. 在Rt△ABC中,∠C=90°,AB=2 , AC= , 则∠B的度数为 .14. 如图,AD∥BE∥CF,且AB=3,AC=8,则的值为 .
13. 在Rt△ABC中,∠C=90°,AB=2 , AC= , 则∠B的度数为 .14. 如图,AD∥BE∥CF,且AB=3,AC=8,则的值为 .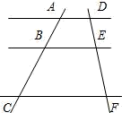 15. 若点A(x1 , y1),点B(x2 , y2)都是反比例函数y=图象上的点,并且y1>y2>0,则x1x2 . (填“>”,“<”或“=”)16. 已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为.17. 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图所示,木杆EF的长为2m,它的影长FD为3m,测得OA为201m,则金字塔的高度BO为 m.
15. 若点A(x1 , y1),点B(x2 , y2)都是反比例函数y=图象上的点,并且y1>y2>0,则x1x2 . (填“>”,“<”或“=”)16. 已知在平面直角坐标系中,△AOB的顶点分别为点A(2,1)、点B(2,0)、点O(0,0),若以原点O为位似中心,相似比为2,将△AOB放大,则点A的对应点的坐标为.17. 据传说,古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理,在金字塔影子的顶部立一根木杆,借助太阳光线构成两个相似三角形,来测量金字塔的高度.如图所示,木杆EF的长为2m,它的影长FD为3m,测得OA为201m,则金字塔的高度BO为 m.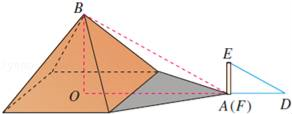 18. 如图,在等腰Rt△ABC中,若∠C=90°,AC=BC=2 . 点D和点E分别是BC边和AB边上两点,连接DE.将△BDE沿DE折叠,得到△B′DE,点B恰好落在AC的中点处,设DE与BB′交于点F,则EF= .
18. 如图,在等腰Rt△ABC中,若∠C=90°,AC=BC=2 . 点D和点E分别是BC边和AB边上两点,连接DE.将△BDE沿DE折叠,得到△B′DE,点B恰好落在AC的中点处,设DE与BB′交于点F,则EF= .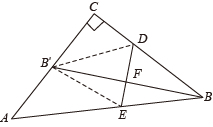
三、解答题
-
19.(1)、计算:(2)、如图是一个几何体的三视图,它的俯视图为菱形.
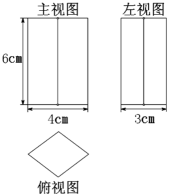
①请写出这个几何体的名称;
②根据所示数据计算这个几何体的体积.
20. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(﹣2,2),B(﹣6,4),C(﹣4,8).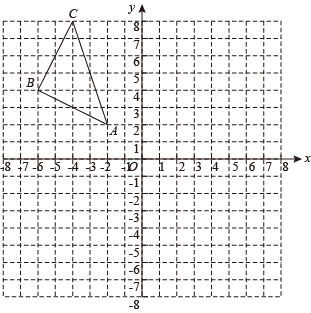
( 1 )画出△ABC关于x轴对称的△A1B1C1;
( 2 )以坐标原点O为位似中心,将△ABC缩小为原来的 , 得到 , 使△ABC与位于位似中心两侧,请在平面直角坐标系中画岀;
( 3 )设△ABC与△的周长分别为、 , 则:= ▲ .
21. 如图,反比例函数(x>0)过点A(3,n),直线AC与x轴交于点C(5,0),tan∠ACO=2,过点C作x轴的垂线交反比例函数图象于点B. (1)、求反比例函数的解析式;(2)、求△ABC的面积.22. 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)
(1)、求反比例函数的解析式;(2)、求△ABC的面积.22. 从一幢建筑大楼的两个观察点A,B观察地面的花坛(点C),测得俯角分别为15°和60°,如图,直线AB与地面垂直,AB=50米,试求出点B到点C的距离.(结果保留根号)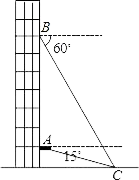 23. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过⊙O上点B的直线交OP的延长线于点C,且CP=CB.
23. 如图,AB是⊙O的弦,OP⊥OA交AB于点P,过⊙O上点B的直线交OP的延长线于点C,且CP=CB.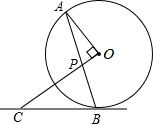 (1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为 , tan∠CBP= . 求BC的长.24. 某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:
(1)、求证:BC是⊙O的切线;(2)、若⊙O的半径为 , tan∠CBP= . 求BC的长.24. 某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)与每件销售价x(元)的关系数据如下:x
30
32
34
36
y
40
36
32
28
(1)、已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);(2)、设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?25. 已知△ABC中,AB=AC,∠BAC=α(α<90°),CD⊥AB于点D,点E是AC边上一动点(不与点C重合),EF⊥BC于点F,EF与CD交于点G.
 (1)、当E点与A点重合时,如图1,若α=45°,猜想CF与EG的数量关系.(2)、当E点与A点不重合时,
(1)、当E点与A点重合时,如图1,若α=45°,猜想CF与EG的数量关系.(2)、当E点与A点不重合时,①若α=45°,如图2,第(1)题中的结论是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
②若α≠45°,如图3,请直接写出的值(用含有α的三角函数表示).
26. 如图,抛物线经过点 , , D为抛物线的顶点.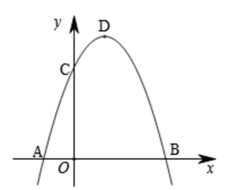 (1)、求抛物线的解析式及顶点坐标;(2)、点C关于抛物线的对称轴的对称点为E点,连接 , , 求tan的值;(3)、在(2)的条件下,点M是抛物线对称轴上一点,且△和△相似,请直接写出点M的坐标.
(1)、求抛物线的解析式及顶点坐标;(2)、点C关于抛物线的对称轴的对称点为E点,连接 , , 求tan的值;(3)、在(2)的条件下,点M是抛物线对称轴上一点,且△和△相似,请直接写出点M的坐标.