吉林省长春市净月高新区2022年九年级一模考试数学试题

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. －2022的相反数是（）

A、－2022 B、2022 C、 $\frac{1}{2022}$ D、－ $\frac{1}{2022}$

查看试题解析
2. 2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，神舟十三号乘组三位航天员翟志刚、王亚平、叶光富进行授课，央视新闻抖音号进行全程直播，某一时刻观看人数达到379.2万，数字3792000用科学记数法可以表示为（）

A、 $3792 \times 1 0^{3}$ B、 $379.2 \times 1 0^{4}$ C、 $3.792 \times 1 0^{6}$ D、 $0.3792 \times 1 0^{7}$

查看试题解析
3. 如图是某个几何体的展开图，该几何体是（）

A、三棱柱 B、四棱柱 C、圆柱 D、圆锥

查看试题解析
4. 不等式 $3 x - 1 > 5$ 的解集是（）

A、 $x > 2$ B、 $x < 2$ C、 $x > \frac{4}{3}$ D、 $x < \frac{4}{3}$

查看试题解析
5. 在平面直角坐标系中，将点 $(- 2, 3)$ 向右平移 $4$ 个单位长度后得到的点的坐标为（）

A、 $(2, 3)$ B、 $(- 6, 3)$ C、 $(- 2, 7)$ D、 $(- 2, - 1)$

查看试题解析
6. 如图是一架人字梯，已知 $A B = A C = 2$ 米，AC与地面BC的夹角为 $α$ ，则两梯脚之间的距离BC为（）

A、 $4 c o s α$ 米 B、 $4 s i n α$ 米 C、 $4 t a n α$ 米 D、 $\frac{4}{c o s α}$ 米

查看试题解析
7. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = B C$ ，按以下步骤作图：①以点A为圆心，以任意长为半径作弧，分别交AC、AB于点M、N；②分别以M、N为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧在 $∠ B A C$ 内交于点O；③作射线AO，交BC于点D．若点D到AB的距离为1，则BC的长为（）

A、1 B、2 C、 $1 + \sqrt{2}$ D、 $2 + 2 \sqrt{2}$

查看试题解析
8. 如图，在平面直角坐标系中，矩形OABC的顶点A在x轴上，顶点B在第一象限，矩形OABC的面积为18，对角线OB上有一点D，点D在反比例函数 $y = \frac{k}{x}$ （ $x > 0$ ）上，若 $O D = 2 B D$ ，则k的值为（）

A、4 B、8 C、9 D、12

查看试题解析

二、填空题

9. 分解因式： $a b - a =$ .

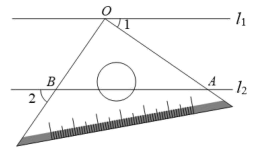
查看试题解析
10. 关于x的一元二次方程 $x^{2} - 6 x + c = 0$ 有两个相等的实数根，则c的值是.

查看试题解析
11. 如图，l₁∥l₂ ，将一个三角板直角顶点O放在直线l₁上，三角板的两条直角边与l₂交于A、B两点，若∠1=35°，则∠2的度数为°．

查看试题解析
12. 如图，点C、D分别是半圆AOB上的三等分点，若半圆的半径OA的长为3，阴影部分的面积是．

查看试题解析
13. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $B D = 8$ ， $A C = 6$ ， $O E / / A B$ ，交 $B C$ 于点E，则 $O E$ 的长为．

查看试题解析
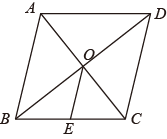14. 圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同．如图，以水平方向为x轴，点O为原点建立平面直角坐标系，点A在y轴上，x轴上的点C、D为水柱的落水点．已知雕塑OA高 $\frac{11}{6}$ 米，与OA水平距离5米处为水柱最高点，落水点C、D之间的距离为22米，则喷出水柱的最大高度为米．

查看试题解析

三、解答题

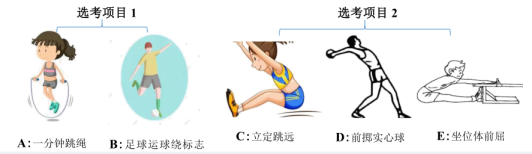
15. 先化简再求值： ${(a - 1)}^{2} - 2 a (a - 1)$ ，其中 $a = \sqrt{3}$ ．

查看试题解析
16. 近几年，参加长春市体育中考考生需进行三个项目测试：①必考项目：男生1000米，女生800米；②选考项目：考生须在以下两类选考项目中，分别选择一项作为考试项目．请用树状图或者列表法表示出一名同学参与“选考项目”的所有可能情况（用字母代替即可），并求出他选择“A：一分钟跳绳和C：立定跳远”的概率，每个项目被选择的可能性相同．

查看试题解析
17. 为保障新冠病毒疫苗接种需求，某生物科技公司开启“加速”模式，生产效率比原先提高了20%，现在生产240万剂疫苗所用的时间比原先生产220万剂疫苗所用的时间少0.5天，问原先每天生产多少万剂疫苗？

查看试题解析
18. 如图，⊙O是 $△ A B C$ 的外接圆，圆心O在AC上．过点B作直线交AC的延长线于点D，使得 $∠ C B D = ∠ C A B$ ．过点A作 $A E ⊥ B D$ 于点E，交⊙O于点F．

(1)、求证：BD是⊙O的切线；

(2)、若 $A C = 4$ ， $s i n D = \frac{2}{3}$ ，则AE的长为．

查看试题解析
19. 第二十四届冬季奥林匹克运动会于2022年2月4日至2月20日在北京举行，为普及青少年冰雪运动项目和知识，越来越多的青少年走向冰场、走进雪场、了解冰雪运动知识．某校开展了一次冬奥知识答题竞赛，七、八年级各有200名学生参加了本次活动，为了解两个年级的答题情况，从两个年级各随机抽取了20名学生的成绩进行调查分析，过程如下（数据不完整）．
收集数据：
七年级 66 70 71 78 71 78 75 78 58 a 63 90 80 85 80 89 85 86 80 87
八年级 61 65 74 70 71 74 74 76 63 b 91 85 80 84 87 83 82 80 86 c
整理、描述数据：
成绩x/分数
七年级成绩统计情况
八年级成绩统计情况
频数
频率
频数
频率
50≤x≤59
1
0.05
0
0
60≤x≤69
2
0.10
3
0.15
70≤x≤79
6
0.30
80≤x≤89
m
10
0.50
90≤x≤99
1
0.05
1
0.05
（说明：成绩80分及以上为优秀，60~79分为合格，60分以下为不合格）
分析数据：两组样本数据的平均数、中位数、众数如表所示：
年级
平均数
中位数
众数
七年级
77.5
79
80
八年级
77.4
n
74
请根据所给信息，解答下列问题：

(1)、a= ， m= ， n=；

(2)、在此次竞赛中，七年级的小冬和八年级的小明都取得了79分，那么的成绩在本年级的排名可能更靠前；（填“小冬”或“小明”）

(3)、估计七年级和八年级此次测试成绩优秀的总人数为．

查看试题解析
20. 如图，在 $5 \times 5$ 的正方形网格中，每个小正方形的顶点称为格点，且每个小正方形的边长均为 $1$ ，线段 $A B$ 的端点在格点上．在图①、图②给定的网格中以 $A B$ 为边各画一个四边形，四边形的顶点都在格点上，并求出所画四边形的面积．

(1)、在图①中画一个正方形，这个正方形的面积为．

(2)、在图②中画一个菱形（与图①所画图形不全等），这个菱形的面积为．

查看试题解析
21. 在一次机器“猫”抓机器“鼠”的展演测试中，“鼠”先从起点出发，1min后，“猫”从同一起点出发去追“鼠”，抓住“鼠”并稍作停留后，“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 $y (m)$ 与时间 $x (m i n)$ 之间的关系如图所示．

(1)、在“猫”追“鼠”的过程中，“猫”的平均速度与“鼠”的平均速度的差是 $m / m i n$ ；

(2)、求 $A B$ 的函数表达式；

(3)、求“猫”从起点出发到返回至起点所用的时间．

查看试题解析
22. 数学兴趣小组在学习平行四边形的性质后，开始进一步的探索．他们将平行四边形沿着它的一条对角线翻折，发现其中还有很多结论：如图①，在平行四边形ABCD中， $A B \neq B C$ ，将 $△ A B C$ 沿AC翻折至 $△ A B^{^{'}} C$ ，连接 $B^{'} D$ ．

(1)、【发现与证明】发现△AB′C与平行四边形ABCD重叠部分的图形始终是____；

A、等腰三角形； B、等边三角形； C、直角三角形

(2)、【应用与探究】求证： $B^{'} D ∥ A C$ ．
如图②，在平行四边形ABCD中，已知 $∠ B = 30 °$ ，将 $△ A B C$ 沿AC翻折至 $△ A B^{^{'}} C$ ，连接 $B^{'} D$ ．若 $A B = \sqrt{3}$ ， $∠ A B^{'} D = 75 °$ ，则 $∠ A C B =$ °， $B C =$ ．

查看试题解析
23. 已知直角三角形ABC中， $∠ C = 90 °$ ， $A C = 6$ ， $A B = 10$ ，动点P从点A出发，以每秒3个单位的速度沿折线 $A B － B C$ 向终点C运动，且不与 $△ A B C$ 的顶点重合，点D为边AB的中点，当点P不与点D重合时，过点P作线段PD的垂线与 $△ A B C$ 的一边交于点Q，构造 $△ Q D P$ ，设点P的运动时间为t（ $t > 0$ ）．

(1)、线段BC的长为．

(2)、点P在线段AB上运动时，用t表示线段PD的长．

(3)、点P在线段AB上运动，当 $△ A D Q$ 是以DQ为腰的等腰三角形时，求t的值．

(4)、当点P经过点D后，作点Q关于PD的对称点为 $Q^{'}$ ，当 $∠ Q D Q^{'} = 2 ∠ B$ 时，直接写出t的值．

查看试题解析
24. 已知抛物线y=x²-2mx+2m+1．

(1)、写出抛物线y=x²-2mx+2m+1的顶点坐标（用含m的式子表示）．

(2)、当x≥1时，y随x的增大而增大，则m的取值范围是．

(3)、当-1≤x≤2时，函数y=x²-2mx+2m+1的图象记为G，设图象G的最低点的纵坐标为y₀ ．当y₀=-1时，求m的值．

(4)、当m＞0时，分别过点A（2，1）、B（2，4）作y轴垂线，垂足分别为点D、点C，抛物线在矩形ABCD内部的图象（包括边界）的最低点到直线y=-2的距离等于最高点到x轴的距离，直接写出m的值．

查看试题解析

成绩x/分数	七年级成绩统计情况		八年级成绩统计情况
成绩x/分数	频数	频率	频数	频率
50≤x≤59	1	0.05	0	0
60≤x≤69	2	0.10	3	0.15
70≤x≤79			6	0.30
80≤x≤89		m	10	0.50
90≤x≤99	1	0.05	1	0.05

年级	平均数	中位数	众数
七年级	77.5	79	80
八年级	77.4	n	74