黑龙江省绥化市肇东十校2022年九年级中考模拟联考数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 为推动世界冰雪运动的发展,我国将于2022年举办北京冬奥会.在此之前进行了冬奥会会标的征集活动,以下是部分参选作品,其文字上方的图案既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 2021年2月25日,习近平总书记庄严宣告,我国脱贫攻坚战取得全面胜利.现标准下,98990000农村贫困人口全部脱贫.数98990000用科学记数法表示为( )A、 B、 C、 D、3. 由4个相同的小正方体搭建了一个积木,从三个方向看积木,所得到的图形如图所示,则这个积木可能是( )
2. 2021年2月25日,习近平总书记庄严宣告,我国脱贫攻坚战取得全面胜利.现标准下,98990000农村贫困人口全部脱贫.数98990000用科学记数法表示为( )A、 B、 C、 D、3. 由4个相同的小正方体搭建了一个积木,从三个方向看积木,所得到的图形如图所示,则这个积木可能是( )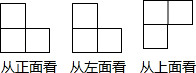 A、
A、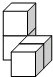 B、
B、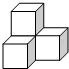 C、
C、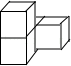 D、
D、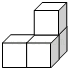 4. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 定义新运算“ ”,规定: .若关于x的不等式 的解集为 ,则m的值是( )A、 B、 C、1 D、26. 下列运算正确的是( )A、 B、 C、 D、(a-2)2=a2-47. 下列命题中,为真命题的是( )
4. 若式子在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 定义新运算“ ”,规定: .若关于x的不等式 的解集为 ,则m的值是( )A、 B、 C、1 D、26. 下列运算正确的是( )A、 B、 C、 D、(a-2)2=a2-47. 下列命题中,为真命题的是( )⑴对角线互相平分的四边形是平行四边形
⑵对角线互相垂直的四边形是菱形
⑶对角线相等的平行四边形是菱形
⑷有一个角是直角的平行四边形是矩形
A、(1)(2) B、(1)(4) C、(2)(4) D、(3)(4)8. 一个多边形的内角和是外角和的4倍,则这个多边形是( )A、六边形 B、八边形 C、十边形 D、十二边形9. 如图是小明某一天测得的7次体温情况的折线统计图,下列信息错误的是( )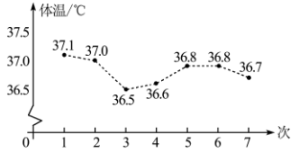 A、测得的最高体温为37.1℃ B、前3次测得的体温在下降 C、这组数据的众数是36.8 D、这组数据的中位数是36.610. 某工厂生产 、 两种型号的扫地机器人. 型机器人比 型机器人每小时的清扫面积多50%;清扫 所用的时间 型机器人比 型机器人多用40分钟. 两种型号扫地机器人每小时分别清扫多少面积?若设 型扫地机器人每小时清扫 ,根据题意可列方程为( )A、 B、 C、 D、11. 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A、测得的最高体温为37.1℃ B、前3次测得的体温在下降 C、这组数据的众数是36.8 D、这组数据的中位数是36.610. 某工厂生产 、 两种型号的扫地机器人. 型机器人比 型机器人每小时的清扫面积多50%;清扫 所用的时间 型机器人比 型机器人多用40分钟. 两种型号扫地机器人每小时分别清扫多少面积?若设 型扫地机器人每小时清扫 ,根据题意可列方程为( )A、 B、 C、 D、11. 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )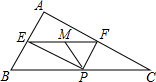 A、5 B、2.5 C、4.8 D、2.412. 如图,在正方形 中,对角线 与 相交于点O,点E在 的延长线上,连接 ,点F是 的中点,连接 交 于点G,连接 ,若 , .则下列结论:① ;② ;③ ;④ ;⑤点D到CF的距离为 .其中正确的结论是( )
A、5 B、2.5 C、4.8 D、2.412. 如图,在正方形 中,对角线 与 相交于点O,点E在 的延长线上,连接 ,点F是 的中点,连接 交 于点G,连接 ,若 , .则下列结论:① ;② ;③ ;④ ;⑤点D到CF的距离为 .其中正确的结论是( )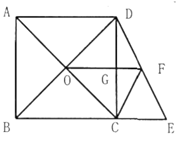 A、①②③④ B、①③④⑤ C、①②③⑤ D、①②④⑤
A、①②③④ B、①③④⑤ C、①②③⑤ D、①②④⑤二、填空题
-
13. 分解因式:= .14. 一个小球在如图所示的方格地砖上任意滚动,并随机停留在某块地砖上.每块地砖的大小、质地完全相同,那么该小球停留在黑色区域的概率是.
 15. 一条弧所对的圆心角为135°,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 cm.16. 若 , 则代数式的值等于 .17. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有 种.18. 已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,则k的值为 .19. 如图,在Rt△ABC中,∠C=90°,点D是AB的中点,点E是线段AC上的动点,BC=4,AB=8,当△ABC和△AED相似时,AE的长为 .
15. 一条弧所对的圆心角为135°,弧长等于半径为5cm的圆的周长的3倍,则这条弧的半径为 cm.16. 若 , 则代数式的值等于 .17. 小明去商店购买A、B两种玩具,共用了10元钱,A种玩具每件1元,B种玩具每件2元.若每种玩具至少买一件,且A种玩具的数量多于B种玩具的数量.则小明的购买方案有 种.18. 已知关于x的方程x2+(2k+1)x+k2-2=0的两实根的平方和等于11,则k的值为 .19. 如图,在Rt△ABC中,∠C=90°,点D是AB的中点,点E是线段AC上的动点,BC=4,AB=8,当△ABC和△AED相似时,AE的长为 .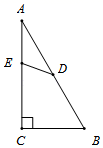 20. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是。
20. 以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是。
21. 如图,点A是反比例函数 图象上一点, 轴于点C且与反比例函数 的图象交于点B , ,连接OA , OB , 若 的面积为6,则 .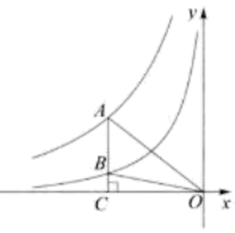 22. 如图都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有7个小圆圈,第②个图形中一共有13个小圆圈,第③个图形中一共有21个小圆圈,…,按此规律排列,则第⑩个图形中小圆圈的个数为 .
22. 如图都是由同样大小的小圆圈按一定规律所组成的,其中第①个图形中一共有7个小圆圈,第②个图形中一共有13个小圆圈,第③个图形中一共有21个小圆圈,…,按此规律排列,则第⑩个图形中小圆圈的个数为 .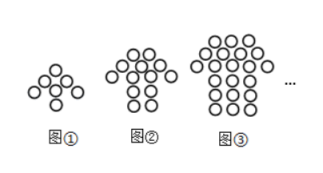
三、解答题
-
23. 如图, 是 的对角线.
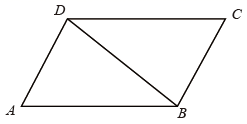 (1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.24. 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
(1)、尺规作图(请用2B铅笔):作线段 的垂直平分线 ,交 , , 分别于 , , ,连接 , (保留作图痕迹,不写作法).(2)、试判断四边形 的形状并说明理由.24. 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
( 1 )画出四边形ABCD旋转180°后的图形;
( 2 )求点C旋转过程中所经过的路径长;
( 3 )求sin∠BAD的值.
25. 如图,在某小区内拐角处的一段道路上,有一儿童在C处玩耍,一辆汽车从被楼房遮挡的拐角另一侧的A处驶来,已知CM=3m,CO=5m,DO=3m,∠AOD=70°,汽车从A处前行多少米才能发现C处的儿童(结果保留整数)?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75;sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)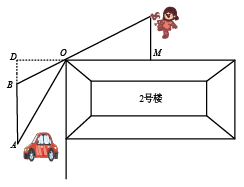 26. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天)之间的关系如图所示.
26. 疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过 天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数 (万人)与各自接种时间 (天)之间的关系如图所示.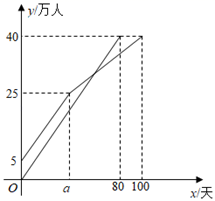 (1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.27. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.
(1)、直接写出乙地每天接种的人数及 的值;(2)、当甲地接种速度放缓后,求 关于 的函数解析式,并写出自变量 的取值范围;(3)、当乙地完成接种任务时,求甲地未接种疫苗的人数.27. 如图,AB为⊙O的直径,C为⊙O上一点,连接AC,BC,D为AB延长线上一点,连接CD,且∠BCD=∠A.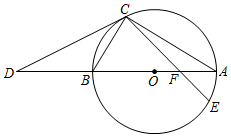 (1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , △ABC的面积为 , 求CD的长;(3)、在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若 , 求BF的长.28. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .
(1)、求证:CD是⊙O的切线;(2)、若⊙O的半径为 , △ABC的面积为 , 求CD的长;(3)、在(2)的条件下,E为⊙O上一点,连接CE交线段OA于点F,若 , 求BF的长.28. 问题解决:如图1,在矩形 中,点 分别在 边上, 于点 .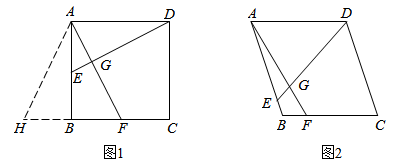 (1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.
(1)、求证:四边形 是正方形;(2)、延长 到点 ,使得 ,判断 的形状,并说明理由.类比迁移:如图2,在菱形 中,点 分别在 边上, 与 相交于点 , ,求 的长.
29. 综合与探究如图,在平面直角坐标系中,抛物线 与x轴交于点A、B , 与y轴交于点C , 连接BC , ,对称轴为 ,点D为此抛物线的顶点.
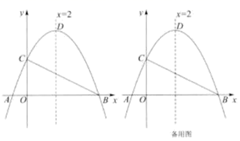 (1)、求抛物线的解析式;(2)、抛物线上C , D两点之间的距离是;(3)、点E是第一象限内抛物线上的动点,连接BE和CE . 求 面积的最大值;(4)、点P在抛物线对称轴上,平面内存在点Q , 使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.
(1)、求抛物线的解析式;(2)、抛物线上C , D两点之间的距离是;(3)、点E是第一象限内抛物线上的动点,连接BE和CE . 求 面积的最大值;(4)、点P在抛物线对称轴上,平面内存在点Q , 使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.