黑龙江省龙东地区2022年九年级第一次模拟数学试题

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $a^{2} + a^{2} = a^{4}$ B、 $a^{6} \div a^{2} = a^{3}$ C、 $a \cdot a^{2} = a^{3}$ D、 ${(2 a^{2})}^{3} = 8 a^{5}$

查看试题解析
2. 下列图形中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图是由若干个相同的小立方体搭成的几何体的主视图和俯视图，则搭成该几何体的小立方体的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 某校九年级有9名同学参加“建党一百周年”知识竞赛，预赛成绩各不相同，要取前5名参加决赛．小兰已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这9名同学成绩的（）

A、中位数 B、众数 C、平均数 D、方差

查看试题解析
5. 如图，在长为10cm，宽为8cm的矩形的四个角上截去四个全等的正方形，使得留下的图形面积是原矩形面积的80%，所截去的小正方形的边长是多少？设小正方形的边长是xcm，下列方程正确的是（）

A、 $(10 - x) (8 - x) = 10 \times 8 \times 80 %$ B、 $(10 - 2 x) (8 - 2 x) = 10 \times 8 \times 80 %$ C、 $(10 - x) (8 - x) = 10 \times 8 \times 20 %$ D、 $10 \times 8 - 4 x^{2} = 10 \times 8 \times 80 %$

查看试题解析
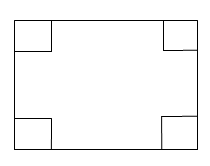6. 已知关于x的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 的解是非负数，则m的取值范围是（　　）

A、m＞2 B、m≥2 C、m≥2且m≠3 D、m＞2且m≠3

查看试题解析
7. 为落实“双减”政策，刘老师把班级里50名学生分成若干小组进行小组互助学习，每小组只能是4人或6人，则分组方案有（）

A、4种 B、3种 C、2种 D、1种

查看试题解析
8. 如图，在平面直角坐标系中，△ABO的边OB与x轴重合，反比例函数y=kx经过线段AB的中点C．若△ABO的面积为6，则k的值为（）

A、6 B、-6 C、3 D、-3

查看试题解析
9. 如图，在平行四边形ABCD中，AB=3，BC=5，BF平分∠ABC交AD于点F，E是AD的中点，连接CE，BF交于点G，连接CF，则 $S_{△ E F G} ： S_{△ C F G}$ 的值为（）

A、 $\frac{1}{5}$ B、 $\frac{1}{9}$ C、 $\frac{1}{10}$ D、 $\frac{1}{20}$

查看试题解析
10. 如图，在正方形ABCD中，以AB为边作等边三角形ABP，连接PD，PC，AC，则下列结论：①∠BCP =75°；② $\frac{P D}{P B} = \frac{\sqrt{3}}{2}$ ；③△ADP和△ABC的面积比为1：2；④ $S_{△ C D P} = \frac{1}{4} C P^{2}$ ．其中结论正确的序号有（）

A、①②④ B、②③④ C、①③④ D、①②③

查看试题解析

二、填空题

11. 2021年5月15日，天问一号探测器成功着陆于火星，我国首次实现地外行星着陆．火星最近距地球5500万千米，数据5500万千米用科学记数法表示为千米．

查看试题解析
12. 函数 $y = \frac{x - 1}{\sqrt{x + 4}}$ 中，自变量x的取值范围是．

查看试题解析
13. 平行四边形 $A B C D$ 的对角线 $A C$ 与 $B D$ 相交于点O， $A C ⊥ B D$ ，请添加一个条件：．使得平行四边形 $A B C D$ 为正方形．

查看试题解析
14. 在一个不透明的袋子中装有除颜色外完全相同的3个白球、1个红球，从中随机摸出1个球，记下颜色，放回搅匀，再随机摸出一个球，则两次摸到的球颜色相同的概率是．

查看试题解析
15. 若关于x的一元一次不等式组 ${\begin{array}{l} 2 x - a ＜ 0 \\ 3 x - 6 ＞ 0 \end{array}$ 无解，则a的取值范围是．

查看试题解析
16. 如图，矩形ABCD与圆心在AB上的☉O交于点G，B，F，E， GB =5，EF =4，那么AD = ．

查看试题解析
17. 一个圆锥的侧面展开图的扇形的圆心角为150度，母线长为12cm，则圆锥的高为cm．

查看试题解析
18. 如图，在 $Rt △ ABC$ 中， $∠ ACB = 90 °$ ， $AC = 6$ ， $BC = 8$ ，AD是 $∠ BAC$ 的平分线.若P，Q分别是AD和AC上的动点，则 $PC + PQ$ 的最小值是.

查看试题解析
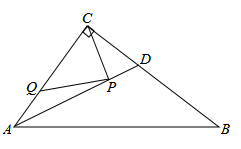19. 已知 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 9$ ， $B C = 12$ ，将它的一条直角边沿一锐角角平分线所在直线翻折，使直角顶点落在斜边上点D处，折痕交另一直角边于点E，则折叠后不重合部分三角形的周长为．

查看试题解析
20. 如图，菱形ABDC 的顶点A(1，1)，B(3，1)，∠BAC=60°，规定把菱形ABDC“先沿y轴翻折，再向下平移1个单位长度”为1次变换，如果这样连续经过2022次变换后，顶点C对应的坐标为．

查看试题解析

三、解答题

21. 先化简，再求值： $(1 + \frac{1}{x - 2}) \div \frac{x^{2} - 2 x + 1}{x - 2}$ ，其中 $x = 2 s i n 30 ° - t a n 45 °$ ．

查看试题解析
22. （2016黑龙江省龙东地区）如图，在平面直角坐标系中，点A、B、C的坐标分别为（﹣1，3）、（﹣4，1）（﹣2，1），先将△ABC沿一确定方向平移得到△A₁B₁C₁ ，点B的对应点B₁的坐标是（1，2），再将△A₁B₁C₁绕原点O顺时针旋转90°得到△A₂B₂C₂ ，点A₁的对应点为点A₂ ．
（ 1 ）画出△A₁B₁C₁；
（ 2 ）画出△A₂B₂C₂；
（ 3 ）求出在这两次变换过程中，点A经过点A₁到达A₂的路径总长．

查看试题解析
23. 如图，抛物线y=ax²+bx+c与直线y=x+3分别交于x轴和y轴上同一点，交点分别是A和C，且抛物线的对称轴为x=-2．

(1)、求抛物线的解析式；

(2)、在直线AC下方的抛物线上找一点D，使△ACD的面积最大，直接写出点D的坐标及最大面积．

查看试题解析
24. 2021年7月，河南多地遭遇百年不遇的洪涝灾害，一方有难，八方支援，全社会各界都向河南捐款捐物，帮助河南人民重建家园．为了解某学校的捐款情况，对学校捐款学生进行了抽样调查，把调查结果制成了如下两幅不完整的统计图，在条形图中，从左到右依次为A.5~15元；B.16~25元；C.26~35元；D.36~45元；E.45元以上（捐款钱数均为整数）．请结合图中数据回答下列问题：

(1)、一共调查了多少名同学？

(2)、补全条形图，并指出中位数落在哪一组；

(3)、若该校3000名学生都参加了捐款活动，估计捐款不少于26元的学生有多少名．

查看试题解析
25. 周末，小畅与妈妈沿相同的路线去爬山．因为乘坐交通工具不同，当小畅到达山脚下开始上山时，妈妈已经到达山顶并开始从山顶返回，在登山的过程中两人一直保持匀速运动，在山路中间有一个观光亭距离山顶30米．两人与观光亭的距离y（单位：m）与小畅登山时间x（单位：min）之间的函数图象如图所示．

(1)、求小畅的速度及b的值；

(2)、求妈妈在下山过程中y与x之间的函数解析式；

(3)、直接写出x为多少时，两人与观光亭的距离相等．

查看试题解析
26. 如图，△ABC与△DEF都是等腰直角三角形，AC=BC，DE=DF．边AB，EF的中点重合于点O，连接BF，CD．

(1)、如图①，当FE⊥AB时，易证BF=CD（不需证明）；
当△DEF绕点O旋转到如图②位置时，猜想BF与CD之间的数量关系，并证明；

(2)、当△ABC与△DEF均为等边三角形时，其他条件不变，如图③，猜想BF与CD之间的数量关系，直接写出你的猜想，不需证明．

查看试题解析
27. 2022年2月第24届冬奥会在北京和张家口举行，中国北京成为世界上首个举办夏季和冬季奥运会的地市．奥运会期间，A，B两地向C，D两地运送物资，已知A，B两地共有物资300吨，其中A地物资是B地物资数量的2倍．现C地需要物资140吨，D地需要物资160吨．从A地往C，D两地运物资的费用分别为10元/吨和15元/吨；从B地往C，D两地运物资的费用分别为8元/吨和15元/吨．设从A地运往C地x吨物资，总运费为y元．

(1)、A地和B地各有多少吨物资？

(2)、求出最少总运费；

(3)、由于更换车型，使A地运往C地的运费每吨减少a（0<a<3）元，这时怎样调运才能使总运费最少？

查看试题解析
28. 如图，在平面直角坐标系中，直线AB的解析式为 $y = \frac{1}{2} x + 3$ ，它与x轴交于点B，与y轴交于点A，直线y=-x与直线AB交于点C．动点P从点C出发，以每秒1个单位长度的速度沿射线CO运动，运动时间为t秒．

(1)、求△AOC的面积；

(2)、设△PAO的面积为S，求S与t的函数关系式，并写出自变量的取值范围；

(3)、M是直线OC上一点，在平面内是否存在点N，使以A，O，M，N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析