黑龙江省哈尔滨市道外区2022年九年级下学期数学调研测试题（一）

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 下列运算正确的是（）

A、 $a^{2} + a = a^{3}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $a^{6} \div a^{2} = a^{4}$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
3. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列几何体是由4个棱长为1的小正方体搭成的，其中左视图面积等于3的是（）

A、 B、 C、 D、

查看试题解析
5. 对于双曲线 $y = \frac{k - 1}{x}$ ，当 $x > 0$ 时，y随x的增大而增大，则k的取值范围是（）.

A、 $k > 1$ B、 $k \geq 1$ C、 $k \leq 1$ D、 $k < 1$

查看试题解析
6. 方程 $\frac{2}{3 x} = \frac{1}{x + 2}$ 的解为（）

A、 $x = - 2$ B、 $x = 4$ C、 $x = 0$ D、 $x = 6$

查看试题解析
7. 某电动自行车厂三月份的产量为1 000辆，由于市场需求量不断增大，五月份的产量提高到l 210辆，则该厂四、五月份的月平均增长率为（）

A、12.1% B、20% C、21% D、10%

查看试题解析
8. 如图，已知 $⊙ O$ 的半径为3， $∠ A O B = 120 °$ ，则 $A B =$ （）

A、 $3 \sqrt{3}$ B、6 C、9 D、 $4 \sqrt{2}$

查看试题解析
9. 将二次函数 $y = 3 {(x - 4)}^{2} + 5$ 的图象向上平移6个单位后得到的函数解析式为（）

A、 $y = 3 {(x - 10)}^{2} + 5$ B、 $y = 3 {(x + 2)}^{2} + 5$ C、 $y = 3 {(x - 4)}^{2} + 11$ D、 $y = 3 {(x - 4)}^{2} - 1$

查看试题解析
10. 如图，△ABC中， $D E ∥ B C$ ， $G F ∥ A C$ ，下列各式错误的是（）

A、 $\frac{A G}{B G} = \frac{C F}{B F}$ B、 $\frac{A D}{A B} = \frac{A E}{A C}$ C、 $\frac{G H}{F H} = \frac{A E}{C E}$ D、 $\frac{F C}{D H} = \frac{A G}{D G}$

查看试题解析

二、填空题

11. 将数20220000用科学记数法表示为．

查看试题解析
12. 在函数 $y = \frac{7}{x + 2}$ 中，自变量x的取值范围是．

查看试题解析
13. 计算： $\sqrt{27} - \sqrt{\frac{1}{3}} =$ .

查看试题解析
14. 把多项式 $m n^{2} - 4 m$ 分解因式的结果为．

查看试题解析
15. 不等式组 ${\begin{array}{l} x - 3 \leq 0 \\ x + 1 > 0 \end{array}$ 的解集为．

查看试题解析
16. 一个扇形的弧长是 $3 π$ cm，半径是5cm，则这个扇形的面积是 cm² ．

查看试题解析
17. 同时抛掷两枚质地均匀的硬币，则两枚硬币全部正面向上的概率是．

查看试题解析
18. 如图，将△ABC绕点A逆时针旋转得到 $△ A B^{'} C^{'}$ ，若点 $B^{'}$ 落到BC边上， $∠ B = 35 °$ ，则 $∠ C B^{'} C^{'} =$ °．

查看试题解析
19. 在△ABC中，AD为高， $∠ A B D = 2 ∠ A C B$ ， $A D = 2$ ， $B D = 1$ ，则 $B C =$ ．

查看试题解析
20. 在△ABC中，点D为AC边的中点， $D E ⊥ A B$ 于点E，△DEF为等边三角形，若 $B E = 3$ ， $A E = 1$ ，则DE的长为．

查看试题解析

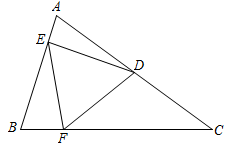
三、解答题

21. 先化简，再求值． $\frac{a}{a^{2} - 1} \div (1 + \frac{1}{a - 1})$ ，其中 $a = 2 c o s 30 ° - t a n 45 °$ ．

查看试题解析
22. 如图，方格纸中每个小正方形的边长均为1，线段AB、CD的端点均在小正方形的顶点上，请按照要求画出下列图形：

(1)、画出△ABE，使得 $∠ A B E = 45 °$ ，且△ABE的面积为5；

(2)、画出以CD为一腰的等腰△CDF，且△CDF的面积为3.5；

(3)、连接EF，直接写出线段EF的长．

查看试题解析
23. 为了推动课堂教学改革，打造高效课堂，某中学对九年级部分学生就一学期以来线上教学方式的支持程度进行调查，下图为根据统计情况绘制的不完整统计图，请根据图中提供的信息，回答下列问题：

(1)、求本次被调查的九年级学生的人数；

(2)、通过计算补全条形统计图；

(3)、该校九年级学生共有540人，请你估计该校九年级有多少名学生支持线上教学方式（含“非常喜欢”和“喜欢”两种情况的学生）？

查看试题解析
24. 如图，已知CD为△ABC中线，E为CD上一点，连接AE并延长至点F，使 $E F = A E$ ，连接BF、CF， $C F ∥ A B$ ．

(1)、求证：四边形DBFC是平行四边形．

(2)、设四边形ABFC的面积为S，在不添加任何辅助线的情况下，请写出图中四个面积等于 $\frac{1}{3} S$ 的三角形．

查看试题解析
25. 某商场购进北京冬奥会甲、乙两种纪念品，若购进甲种纪念品1件、乙种纪念品2件，需170元，若购进甲种纪念品2件、乙种纪念品1件，需295元．

(1)、甲、乙两种纪念品每件各需要多少元？

(2)、商场决定购进甲、乙两种纪念品若干件，购进甲种纪念品比购进乙种纪念品多用45元，且购进两种纪念品的总资金不超过8355元，则最多购进甲种纪念品多少件？

查看试题解析
26. 已知AB为 $⊙ O$ 直径，△PCD是 $⊙ O$ 内接三角形， $A B = \sqrt{2} C D$ ．

(1)、如图1，求 $∠ P$ 的度数；

(2)、如图2，PD交AB于点M，作 $C E ⊥ A B$ 交AB于点E，连接CO并延长交PD于点N，若CP平分 $∠ E C O$ ，求证： $O M = O N$ ；

(3)、如图3，在（2）的条件下，F是 $⊙ O$ 外一点，FC是 $⊙ O$ 的切线，FD∥PC，若 $C F - C O = \frac{2}{3} O N$ ， $A E = 2$ ，求PD的长．

查看试题解析
27. 如图，在平面直角坐标系中，点O为坐标原点，抛物线 $y = a (x + 3) (x - 5) (a > 0)$ 交x轴于A、B两点（A左B右），交y轴于点C，且 $3 O C = 5 O A$ ．

(1)、求抛物线解析式；

(2)、点P为第一象限抛物线上一点，连接PA交y轴于点D，设P点横坐标为m，△ACD的面积为S，求S与m之间的函数关系式；

(3)、在（2）的条件下，点E为线段PD上一点，连接BE、CE，当 $∠ C E B = 45 °$ ，且△ACD的面积为 $\frac{21}{2}$ 时，求点E的坐标．

查看试题解析