黑龙江省大庆市肇源县2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 中国疫苗撑起全球抗疫“生命线”!中国外交部数据显示,截止2021年3月底,我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能有望达到50亿剂,约占全球产能的一半,必将为全球抗疫作出重大贡献.数据“50亿”用科学记数法表示为( )A、 B、 C、 D、3. 如图,△DEF是由△ABC绕点O旋转180°而得到的,则下列结论不成立的是( )
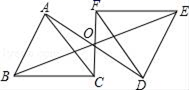 A、点A与点D是对应点 B、BO=EO C、∠ACB=∠FDE D、AB∥DE4. 下列说法错误的是( )A、 的平方根是 B、 的算术平方根是4 C、0的立方根是0 D、64的立方根是5. 一次函数和反比例函数的图象如图所示,若 , 则x的取值范围是( )
A、点A与点D是对应点 B、BO=EO C、∠ACB=∠FDE D、AB∥DE4. 下列说法错误的是( )A、 的平方根是 B、 的算术平方根是4 C、0的立方根是0 D、64的立方根是5. 一次函数和反比例函数的图象如图所示,若 , 则x的取值范围是( ) A、或 B、 C、或 D、或6. 如图,转盘中四个扇形的面积都相等.小明随意转动转盘1次,指针指向的数字为偶数的概率为( )
A、或 B、 C、或 D、或6. 如图,转盘中四个扇形的面积都相等.小明随意转动转盘1次,指针指向的数字为偶数的概率为( )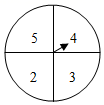 A、 B、 C、 D、7. 如图,中, , , 的垂直平分线交于D,连接 , 若 , 则的长为( )
A、 B、 C、 D、7. 如图,中, , , 的垂直平分线交于D,连接 , 若 , 则的长为( )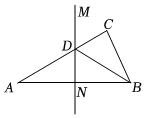 A、 B、 C、 D、8. 已知关于x的一元二次方程 , 其中a、b、c分别为三边的长.
A、 B、 C、 D、8. 已知关于x的一元二次方程 , 其中a、b、c分别为三边的长.①如果是方程的根,则是等腰三角形;
②如果方程有两个相等的实数根,则是等边三角形;
③如果是等边三角形,则这个一元二次方程的根为和 .
其中正确的是( )
A、① B、①③ C、①② D、②③9. 如图,斗笠是一种遮挡阳光和蔽雨的编结帽,它可近似看成一个圆锥,已知该斗笠的侧面积为 , 是斗笠的母线,长为 , 为斗笠的高,为斗笠末端各点所在圆的直径,则的值为( ) A、 B、 C、 D、10. 下列关于函数 的四个命题:①当 时, 有最小值10;② 为任意实数, 时的函数值大于 时的函数值;③若 ,且 是整数,当 时, 的整数值有 个;④若函数图象过点 和 ,其中 , ,则 .其中真命题的序号是( )
A、 B、 C、 D、10. 下列关于函数 的四个命题:①当 时, 有最小值10;② 为任意实数, 时的函数值大于 时的函数值;③若 ,且 是整数,当 时, 的整数值有 个;④若函数图象过点 和 ,其中 , ,则 .其中真命题的序号是( )
A、① B、② C、③ D、④二、填空题
-
11. 使分式 有意义的x的取值范围是.12. 将多项式分解因式为 .13. 一元二次方程的两根为、 , 则 .14. 甲、乙两名同学进行跳高测试,每人10次跳高的平均成绩恰好是1.6米,方差分别是S甲2=1.2,S乙2=0.5,则在本次测试中,同学的成绩更稳定(填“甲”或“乙”)15. 给你一个任意数,按下列程序进行计算,写出输出结果 .
 16. 如图,在ABC中,AB=6,BC=12,点P是AB边的中点,点Q是BC边上一个动点,当BQ=时,BPQ与BAC相似.
16. 如图,在ABC中,AB=6,BC=12,点P是AB边的中点,点Q是BC边上一个动点,当BQ=时,BPQ与BAC相似. 17. 如图,在直角坐标系中,矩形的顶点O在坐标原点,边在x轴上,在y轴上,B的坐标是 , 如果以点O为位似中心,将矩形缩小为原来的 , 那么点B的对应点的坐标是 .
17. 如图,在直角坐标系中,矩形的顶点O在坐标原点,边在x轴上,在y轴上,B的坐标是 , 如果以点O为位似中心,将矩形缩小为原来的 , 那么点B的对应点的坐标是 .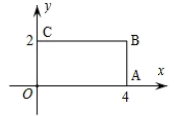 18. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .
18. 有一架竖直靠在直角墙面的梯子正在下滑,一只猫紧紧盯住位于梯子正中间的老鼠,等待与老鼠距离最小时扑捉.把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点,模型如图, ,点 , 分别在射线 , 上, 长度始终保持不变, , 为 的中点,点 到 , 的距离分别为4和2.在此滑动过程中,猫与老鼠的距离 的最小值为 .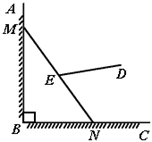
三、解答题
-
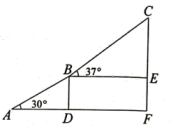
19. 计算:20. 先将分式(1+ )÷ 进行化简,然后请你给x选择一个合适的值,求原式的值.21. 已知方程组 的解也是关于x、y的方程 的一个解,求a的值.22. 2022年冬季奥运会在北京举行,激起了人们对冰雪运动的极大热情.如图是某滑雪场高级雪道缆车线路示意图,滑雪者从点出发,途经点后到达终点 , 其中 , , 且段的运行路线与水平面的夹角为30°,段的运行路线与水平面的夹角为37°,求从点运行到点垂直上升的高度.(结果保留整数;参考数据: , , )
 23. 中华文化源远流长,文学方面,西游记、三国演义、水浒传、红楼梦是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图尚不完整的统计图.
23. 中华文化源远流长,文学方面,西游记、三国演义、水浒传、红楼梦是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图尚不完整的统计图.
请根据以上信息,解决下列问题:
(1)、本次调查所得数据的众数是部,中位数是部;(2)、请将条形统计图补充完整;(3)、没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,请用列表或画树状图的方法求他们恰好选中同一名著的概率.24. 如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE。
 (1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.25. 如图,在平面直角坐标系xOy内,函数y=的图象与反比例函数y=(k≠0)图象有公共点A,点A的坐标为(8,a),AB⊥x轴,垂足为点B.
(1)、求证:四边形ABCD是菱形;(2)、若AB= ,BD=2,求OE的长.25. 如图,在平面直角坐标系xOy内,函数y=的图象与反比例函数y=(k≠0)图象有公共点A,点A的坐标为(8,a),AB⊥x轴,垂足为点B. (1)、求反比例函数的解析式;(2)、点P在线段OB上,若AP=BP+2,求线段OP的长;(3)、点D为射线OA上一点,在(2)的条件下,若S△ODP=S△ABO , 求点D的坐标.26. 某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)、经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得512元的利润,每件应降价多少元?27. 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.
(1)、求反比例函数的解析式;(2)、点P在线段OB上,若AP=BP+2,求线段OP的长;(3)、点D为射线OA上一点,在(2)的条件下,若S△ODP=S△ABO , 求点D的坐标.26. 某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.(1)、若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;(2)、经调查,若该商品每降价0.5元,每天可多销售4件,那么每天要想获得512元的利润,每件应降价多少元?27. 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D. (1)、求证:
(1)、求证:①BC是⊙O的切线;
②;
(2)、若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.28. 如图,抛物线 与直线 相交于 , 两点,且抛物线经过点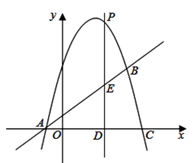 (1)、求抛物线的解析式.(2)、点P是抛物线上的一个动点(不与点 点 重合),过点P作直线 轴于点D,交直线AB于点E.当 时,求P点坐标;(3)、如图所示,设抛物线与 轴交于点F,在抛物线的第一象限内,是否存在一点Q,使得四边形OFQC的面积最大?若存在,请求出点Q的坐标;若不存在,说明理由.
(1)、求抛物线的解析式.(2)、点P是抛物线上的一个动点(不与点 点 重合),过点P作直线 轴于点D,交直线AB于点E.当 时,求P点坐标;(3)、如图所示,设抛物线与 轴交于点F,在抛物线的第一象限内,是否存在一点Q,使得四边形OFQC的面积最大?若存在,请求出点Q的坐标;若不存在,说明理由.