广东省中山市小榄镇2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. ﹣2的相反数是( )A、2 B、﹣2 C、 D、±22. 一个几何体,如图所示,则它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 0.000345用科学记数法表示为( )A、0.345×10﹣3 B、3.45×104 C、3.45×10﹣4 D、34.5×10﹣54. 不等式组的最大整数解为( )A、1 B、 C、0 D、5. 下列运算中,计算正确的是( )A、 B、 C、 D、6. 将一副三角板(含30°、45°、60°)按如图所示的位置摆放在直尺上,则的度数为( )
3. 0.000345用科学记数法表示为( )A、0.345×10﹣3 B、3.45×104 C、3.45×10﹣4 D、34.5×10﹣54. 不等式组的最大整数解为( )A、1 B、 C、0 D、5. 下列运算中,计算正确的是( )A、 B、 C、 D、6. 将一副三角板(含30°、45°、60°)按如图所示的位置摆放在直尺上,则的度数为( )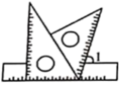 A、75° B、60° C、105° D、95°7. 把二次函数的图象向左平移1个单位,然后向上平移3个单位,则平移后的图象对应的二次函数的关系式为( )A、 B、 C、 D、8. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
A、75° B、60° C、105° D、95°7. 把二次函数的图象向左平移1个单位,然后向上平移3个单位,则平移后的图象对应的二次函数的关系式为( )A、 B、 C、 D、8. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )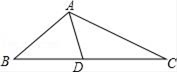 A、4 B、4 C、6 D、49.
A、4 B、4 C、6 D、49.如图,△ABC中,AB=AC,BD=CE,BE=CF,若∠A=40°,则∠DEF的度数是( )
 A、75° B、70° C、65° D、60°10. 定义新运算“※”:对于实数m,n,p,q,有 ,其中等式右边是通常的加法和乘法运算,如: .若关于x的方程 有两个实数根,则k的取值范围是( )A、 且 B、 C、 且 D、
A、75° B、70° C、65° D、60°10. 定义新运算“※”:对于实数m,n,p,q,有 ,其中等式右边是通常的加法和乘法运算,如: .若关于x的方程 有两个实数根,则k的取值范围是( )A、 且 B、 C、 且 D、二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 因式分解: = .13. 已知 , 两点在双曲线上,且 , 则m的取值范围是 .14. 如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B, , 若四边形BCED的面积为7,则△ADE的面积为.
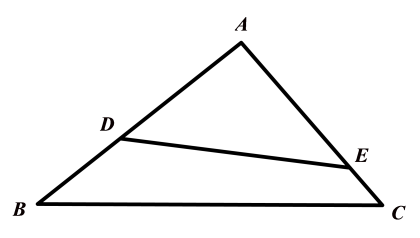 15. 如图,直线l与x轴,y轴分别交于A、B两点,且与反比例函数y=(x<0)的图象交于点C,若=1,则k= .
15. 如图,直线l与x轴,y轴分别交于A、B两点,且与反比例函数y=(x<0)的图象交于点C,若=1,则k= . 16. 实数m满足 , 且 , 那么 .17. 如图,在中, , , 于点D,于点E, . 连接DE,过点D作交BE于点F,则DF长度为 .
16. 实数m满足 , 且 , 那么 .17. 如图,在中, , , 于点D,于点E, . 连接DE,过点D作交BE于点F,则DF长度为 .
三、解答题
-
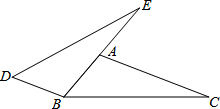
18. 计算: .19. 先化简,再求值: , 其中a满足 .20. 已知:如图,点A、B、E在同一直线上,AC∥BD且AC=BE,∠ABC=∠D.
求证:AB=BD.
 21. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2018年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2021年起加快绿化速度,要求不超过3年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?22. 如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即 , 点B、F在线段AC上,点C在DE上,支杆cm, , , 。请根据以上信息,解决下列问题:
21. 某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2018年初开始实施后,实际每年绿化面积是原计划的1.5倍,这样可提前4年完成任务.(1)、实际每年绿化面积为多少万平方米?(2)、为加大创建力度,市政府决定从2021年起加快绿化速度,要求不超过3年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?22. 如图1,图2分别是网上某种型号拉杆箱的实物图与示意图,根据商品介绍,获得了如下信息:滑杆DE、箱长BC、拉杆AB的长度都相等,即 , 点B、F在线段AC上,点C在DE上,支杆cm, , , 。请根据以上信息,解决下列问题: (1)、求AC的长度(结果保留根号);(2)、求拉杆端点A到水平滑杆ED的距离(结果保留根号).23. 如图,反比例函数的图像与一次函数的图像交于、两点.
(1)、求AC的长度(结果保留根号);(2)、求拉杆端点A到水平滑杆ED的距离(结果保留根号).23. 如图,反比例函数的图像与一次函数的图像交于、两点. (1)、求一次函数的解析式及的面积;(2)、若点P是x轴正半轴上一点,连接AP、BP,当是以AB为腰的等腰三角形时,请直接写出点P的坐标.24. 已知在中,P是CD的中点,B是AD延长线上的一点,连接BC,AP.
(1)、求一次函数的解析式及的面积;(2)、若点P是x轴正半轴上一点,连接AP、BP,当是以AB为腰的等腰三角形时,请直接写出点P的坐标.24. 已知在中,P是CD的中点,B是AD延长线上的一点,连接BC,AP. (1)、如图1,若 , , , .
(1)、如图1,若 , , , .①求证:是等边三角形;
②求BC的长;
(2)、过点D作 , 交AP延长线于点E,如图2所示.若 , . 求证 .25. 如图,在平面直角坐标系中,抛物线与x轴交于点 , 点 , 与y轴交于点C,连接BC,又已知位于y轴右侧且垂直于x轴的动直线l,沿x轴正方向从O运动到B(不含O点和B点),且分别交抛物线,线段BC以及x轴于点P、D、E. (1)、求抛物线的表达式;(2)、连接AC,AP,当直线l运动时,求使得和相似的点P的坐标;(3)、作 , 垂足为F,当直线l运动时,求面积的最大值.
(1)、求抛物线的表达式;(2)、连接AC,AP,当直线l运动时,求使得和相似的点P的坐标;(3)、作 , 垂足为F,当直线l运动时,求面积的最大值.