北京市通州区2022年中考数学一模试卷

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列几何体中，其俯视图是三角形的是（）

A、 B、 C、 D、

查看试题解析
2. 2022年3月，在第十三届全国人民代表大会第五次会议上，国务院总理李克强在政府工作报告中指出：2021年，我国经济保持恢复发展，国内生产总值达到1140000亿元，增长8.1%．将1140000用科学记数法表示应为（）

A、 $0.114 \times 1 0^{7}$ B、 $1.14 \times 1 0^{7}$ C、 $1.14 \times 1 0^{6}$ D、 $11.4 \times 1 0^{5}$

查看试题解析
3. 2022年北京和张家口成功举办了第24届冬奥会和冬残奥会．下面关于奥运会的剪纸图片中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 实数a在数轴上的对应点的位置如图所示，那么下列结论正确的是（）

A、 $| a | > 1$ B、 $- a < 1$ C、 $a + 1 > 0$ D、 $\frac{1}{a} < - 1$

查看试题解析
5. 如果甲、乙、丙三位同学随机站成一排，那么甲站在中间的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{6}$ C、 $\frac{2}{3}$ D、 $\frac{1}{3}$

查看试题解析
6. 如图，已知 $∠ 1 + ∠ 2 + ∠ 3 = 240 °$ ，那么∠4的度数为（）

A、 $60 °$ B、 $120 °$ C、 $130 °$ D、 $150 °$

查看试题解析
7. 已知a、b表示下表第一行中两个相邻的数，且 $a < \sqrt{13} < b$ ，那么a的值是（）
x
3
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
4
$x^{2}$
9
9.61
10.24
10.89
11.56
12.25
12.96
13.69
14.44
15.21
16

A、3.5 B、3.6 C、3.7 D、3.8

查看试题解析
8. 如图，正方形ABCD的边长是4，E是AB上一点，F是延长线上的一点，且BE＝DF，四边形AEGF是矩形，设BE的长为x，AE的长为y，矩形AEGF的面积为S，则y与x，S与x满足的函数关系分别是（）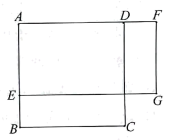

A、一次函数关系，二次函数关系 B、反比例函数关系，二次函数关系 C、一次函数关系，反比例函数关系 D、反比例函数关系，一次函数关系

查看试题解析

二、填空题

9. 若分式 $\frac{x + 1}{x - 1}$ 的值为0，则x的值是．

查看试题解析
10. 分解因式： $a x^{2} - 9 a =$ .

查看试题解析
11. 如图所示，某种“视觉减速带”是由三个形状完全相同，颜色不同的菱形拼成，可以让平面图形产生立体图形般的视觉效果．则 $∠ 1$ 的度数为．

查看试题解析
12. 方程组 ${\begin{array}{l} x + y = 1 \\ x - y = 3 \end{array}$ 的解是.

查看试题解析
13. 如图，PA，PB是 $⊙ O$ 的切线，切点分别为A，B，连接OB，AB．如果 $∠ O B A = 20 °$ ，那么∠P的度数为．

查看试题解析
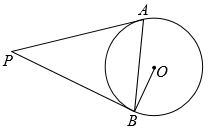14. 如果关于x的方程 $x^{2} + 6 x + m = 0$ 有两个相等的实数根，那么m的值是，方程的根是．

查看试题解析
15. 如图，在△ABC中点D在AB上（不与点A，B重合），连接CD．只需添加一个条件即可证明△ACD与△ABC相似，这个条件可以是（写出一个即可）．

查看试题解析
16. 某学习兴趣小组由学生和教师组成，人员构成同时满足以下三个条件：
（i）男学生人数多于女学生人数；
（ii）女学生人数多于教师人数；
（iii）教师人数的两倍多于男学生人数
①若教师人数为4，则女学生人数的最大值为；
②该小组人数的最小值为．

查看试题解析

三、解答题

17. 计算： $| - 3 | - 2 t a n 60 ° + {(\frac{1}{2})}^{- 1} + \sqrt{12}$ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 3 x - 1 > x + 1 \\ \frac{4 x - 5}{3} \leq x \end{array}$

查看试题解析
19. 已知 $a^{2} - a b = 1$ ，求代数式 $(a - b)^{2} + (a + b) (a - b)$ 的值．

查看试题解析
20. 已知：如图，△ABC为锐角三角形，AB＝AC．
求作：点P，使得AP＝AB，且 $∠ A P C = ∠ B A C$ ．
作法：①以点A为圆心，AB长为半径画圆；
②以点B为圆心，BC长为半径画弧，交 $⊙ A$ 于点D（异于点C）；
③连接DA并延长交 $⊙ A$ 于点P．
所以点P就是所求作的点．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接PC．
∵AB＝AC，
∴点C在 $⊙ A$ 上．
∵ $\overset{⌢}{D C} = \overset{⌢}{D C}$ ，
∴ $∠ D P C = \frac{1}{2} ∠ D A C$ （）（填推理的依据），
由作图可知， $\overset{⌢}{B D} = \overset{⌢}{B C}$ ，
∴ $∠ D A B =$ ▲ $= \frac{1}{2} ∠ D A C$ ．
∴ $∠ A P C = ∠ B A C$ ．

查看试题解析
21. 已知一次函数 $y_{1} = 2 x + m$ 的图象与反比例函数 $y_{2} = \frac{k}{x} (k > 0)$ 的图象交于A，B两点．

(1)、当点A的坐标为 $(2 ， 1)$ 时．
①求m，k的值；
②当 $x > 2$ 时， $y_{1}$ _▲_ $y_{2}$ （填“ $>$ ”“ $=$ ”或“ $<$ ”）．

(2)、将一次函数 $y_{1} = 2 x + m$ 的图象沿y轴向下平移4个单位长度后，使得点A，B关于原点对称，求m的值

查看试题解析
22. 如图．在△ABC中，AB＝BC，BD平分∠ABC交AC于点D．点E为AB的中点，连接DE，过点E作 $E F ∥ B D$ 交CB的延长线于点F．

(1)、求证：四边形DEFB是平行四边形；

(2)、当AD＝4，BD＝3时，求CF的长．

查看试题解析

23. 如图1是某条公路的一个单向隧道的横断面．经测量，两侧墙AD和与路面AB垂直，隧道内侧宽AB＝4米．为了确保隧道的安全通行，工程人员在路面AB上取点E，测量点E到墙面AD的距离和到隧道顶面的距离EF．设

A E = x

米，

E F = y

米．通过取点、测量，工程人员得到了x与y的几组值，如下表：

x（米）	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
y（米）	3.00	3.44	3.76	3.94	3.99	3.92	3.78	3.42	3.00

(1)、隧道顶面到路面AB的最大高度为米；

(2)、请你帮助工程人员建立平面直角坐标系，描出上表中各对对应值为坐标的点，画出可以表示隧道顶面的图象．

(3)、今有宽为2.4米，高为3米的货车准备在隧道中间通过（如图2）．根据隧道通行标准，其车厢最高点到隧道顶面的距离应大于0.5米．结合所画图象，请判断该货车是否安全通过：（填写“是”或“否”）．

查看试题解析

24. 2021年，我国粮食总产量再创新高．小刘同学登录国家统计局网站，查询到了我国2021年31个省、直辖市、自治区的粮食产量数据（万吨）．并对数据进行整理、描述和分析．下面给出了部分信息．
a．反映2021年我国31个省、直辖市、自治区的粮食产量数据频数分布直方图如图（数据分成8组： $0 \leq x < 1000$ ， $1000 \leq x < 2000$ ， $2000 \leq x < 3000$ ， $3000 \leq x < 4000$ ， $4000 \leq x < 5000$ ， $5000 \leq x < 6000$ ， $6000 \leq x < 7000$ ， $7000 \leq x \leq 8000$ ）：

b.2021年我国各省、直辖市、自治区的粮食产量在 $1000 \leq x < 2000$ 这一组的是：
10928，1094.9，1231.5，1270.4，1279.9，1386.5，1421.2，1735.8，1930.3

(1)、2021年我国各省、直辖市、自治区粮食产量的中位数为万吨；

(2)、小刘同学继续收集数据的过程中，发现北京市与河南省的单位面积粮食产量（千克/公顷）比较接近，如下图所示，他将自2016年至2021年北京市与河南省的单位面积粮食产量表示出来：
（ $单位面积粮食产量 = \frac{粮食总产量}{播种面积}$ ）

自2016－2021年间，设北京市单位面积粮食产量的平均值为 ${\bar{x}}_{A}$ ，方差为 $S_{A}^{2}$ ；河南省单位面积粮食产量的平均值为 ${\bar{x}}_{B}$ ，方差为 $S_{B}^{2}$ ；则 ${\bar{x}}_{A}$ ${\bar{x}}_{B}$ ， $S_{A}^{2}$ $S_{B}^{2}$ （填写“”或“＜”）；

(3)、国家统计局公布，2021年全国粮食总产量13657亿斤，比上一年增长2.0%．如果继续保持这个增长率，计算2022年全国粮食总产量约为多少亿斤（保留整数）．

查看试题解析
25. 如图1，AB是 $⊙ O$ 的直径，点C是 $⊙ O$ 上不同于A，B的点，过点C作 $⊙ O$ 的切线为BA的延长线交于点D，连接AC，BC．

(1)、求证： $∠ D C A = ∠ B$ ；

(2)、如图2，过点C作 $C E ⊥ A B$ 于点E，交 $⊙ O$ 于点F，FO的延长线交CB于点G．若 $⊙ O$ 的直径为4， $∠ D = 30 °$ ，求线段FG的长．

查看试题解析
26. 已知抛物线 $y = a x^{2} - 4 a x + 2 (a \neq 0)$ 过 $A (- 1 ， m)$ ， $B (2 ， n)$ ， $C (3 ， p)$ 三点．

(1)、求n的值（用含有a的代数式表示）；

(2)、若 $m n p < 0$ ，求a的取值范围．

查看试题解析
27. 如图，在 $R t △ A C B$ 中，∠ACB＝90°，AC＝BC．点D是BC延长线上一点，连接AD．将线段AD绕点A逆时针旋转90°，得到线段AE．过点E作 $E F ∥ B D$ ，交AB于点F．

(1)、①直接写出∠AFE的度数是 ▲ ；
②求证：∠DAC＝∠E；

(2)、用等式表示线段AF与DC的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，给出如下定义：点P为图形G上任意一点，将点P到原点O的最大距离与最小距离之差定义为图形G的“全距”．特别地，点P到原点O的最大距离与最小距离相等时，规定图形G的“全距”为0．

(1)、如图，点 $A (- \sqrt{3} ， 1)$ ， $B (\sqrt{3} ， 1)$ ．
①原点O到线段AB上一点的最大距离为，最小距离为；

②当点C的坐标为 $(0 ， m)$ 时，且 $△ A B C$ 的“全距”为1，求m的取值范围；

(2)、已知OM＝2，等边△DEF的三个顶点均在半径为1的 $⊙ M$ 上．请直接写出△DEF的“全距”d的取值范围．

查看试题解析

x	3	3.1	3.2	3.3	3.4	3.5	3.6	3.7	3.8	3.9	4
$x^{2}$	9	9.61	10.24	10.89	11.56	12.25	12.96	13.69	14.44	15.21	16