北京市顺义区2022年中考数学一模试卷

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 北京冬奥会期间，共有近1.9万名赛会志愿者和20余万人次城市志愿者参与服务，他们默默奉献并积极传递正能量，共同用实际行动生动地诠释了“奉献、友爱、互助、进步”的志愿精神．将1.9万用科学记数法表示应为（）

A、 $19 \times 1 0^{3}$ B、 $1.9 \times 1 0^{3}$ C、 $1.9 \times 1 0^{4}$ D、 $0.19 \times 1 0^{5}$

查看试题解析
2. 一个几何体的三视图如图所示，该几何体是（）

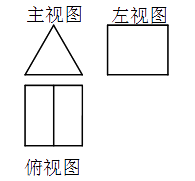A、直三棱柱 B、长方体 C、圆锥 D、立方体

查看试题解析
3. 实数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A、 $a + 2 > 0$ B、 $| a | > b$ C、 $a + b > 0$ D、 $a b > 0$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{2} + 2 a^{2} = 3 a^{4}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 $(a^{2})^{3} = a^{5}$ D、 $(a b)^{2} = a^{2} b^{2}$

查看试题解析
5. 如图，直线 $a ∥ b$ ，点B在直线a上， $A B ⊥ B C$ ，若∠1=40°，则∠2的度数为（）

A、40° B、50° C、80° D、140°

查看试题解析
6. 下列采用的调查方式中，合适的是（）

A、为了解潮白河的水质情况，采用抽样调查的方式 B、某工厂为了解所生产的产品的合格率，采用普查的方式 C、某小型企业给在职员工做工作服前进行尺寸大小的调查，采用抽样调查的方式 D、为了解神舟飞船设备零件的质量情况，采用抽样调查的方式

查看试题解析
7. 如图，小明从A点出发，沿直线前进20米后左转30°，再沿直线前进20米，又向左转30°，…，照这样走下去，他第一次回到出发地A点时，一共走了（）

A、120米 B、200米 C、160米 D、240米

查看试题解析
8. 如图1，点P从△ABC的顶点B出发，沿 $B \to C \to A$ 匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M是曲线部分的最低点，则△ABC的面积是（）

A、30 B、60 C、78 D、156

查看试题解析

二、填空题

9. 若二次根式 $\sqrt{x - 2}$ 在实数范围内有意义，则实数 $x$ 的取值范围是.

查看试题解析
10. 分解因式： $3 x^{3} - 12 x =$ .

查看试题解析
11. 如果 $a + b = 2$ ，那么代数式 $(\frac{a^{2} + b^{2}}{b} + 2 a) \cdot \frac{2 b}{a + b}$ 的值为．

查看试题解析
12. 已知点 $A (1 ， y_{1})$ ， $B (3 ， y_{2})$ 在反比例函数 $y = \frac{m - 2}{x}$ 的图象上，且 $y_{1} < y_{2}$ ，则m的取值范围是．

查看试题解析
13. .如图，在 Rt△ABC中，∠B＝90°，以点 A 为圆心，适当长为半径画弧，分别交AB、AC 于点 D，E，再分别以点 D、E 为圆心，大于 $\frac{1}{2}$ DE 为半径画弧，两弧交于点F，作射线AF交边BC于点G，若 BG＝1，AC＝4，则△ACG 的面积是.

查看试题解析
14. 中共中央办公厅、国务院办公厅印发了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》（简称“双减”）．为全面落实“双减”工作，某校成立了三个义务宣讲团，为学生家长做双减政策解读．现招募宣讲教师，如果张老师和李老师每人随机选报其中的一个宣讲团，则他们恰好选到同一个宣讲团的概率是．

查看试题解析
15. 《九章算术》之“粟米篇”中记载了中国古代的“粟米之法”：“粟率五十，粝米三十……”（粟指带壳的谷子，粝米指糙米），其意为：“50单位的粟，可换得30单位的粝米……”问题：有3斗的粟（1斗＝10升），若按照此“粟米之法”，则可以换得粝米为升．

查看试题解析
16. 如图，矩形ABCD中，AB=2，BC=1，将矩形ABCD绕顶点C顺时针旋转90°，得到矩形EFCG，连接AE，取AE的中点H，连接DH，则 $D H =$ ．

查看试题解析

三、解答题

17. 计算： $2 t a n 60 ° - \sqrt{27} + {(\frac{1}{2})}^{- 2} + | 1 - \sqrt{3} |$ ．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 2 (x + 1) \leq 5 x + 8 \\ 2 x - 5 < \frac{x - 1}{2} \end{array}$ ，并写出它的所有整数解．

查看试题解析
19. 已知：如图， $∠ A O B$ 和射线PN．
求作：射线PM，使得 $∠ M P N = 2 ∠ A O B$ ．
作法：①在射线OB上任取一点C，以点C为圆心，OC的长为半径画弧，交OA于点D；
②以点P为圆心，OC的长为半径画圆，交射线PN的反向延长线于点E；
③以点E为圆心，OD的长为半径画弧，在射线PN上方，交OP于点M；
④作射线PM．
所以射线PM就是所求作的射线．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接CD，EM．
∵PM=PE=CD=CO，EM=OD，
∴ $△ M E P ≌ △ D O C$ （）（填推理依据）．
∴ $∠ M E P = ∠ D O C$ ．
又∵ $∠ M P N = 2 ∠ M E P$ （）（填推理依据）．
∴ $∠ M P N = 2 ∠ A O B$ ．

查看试题解析
20. 已知关于x的一元二次方程 $m x^{2} - (2 m - 1) x + m - 2 = 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、若方程有一个根是0，求方程的另一个根．

查看试题解析
21. 如图，在四边形ABCD中， $A D ∥ B C$ ， $A C ⊥ B D$ ，垂足为O，过点D作BD的垂线交BC的延长线于点E．

(1)、求证：四边形ACED是平行四边形；

(2)、若AC=4，AD=2， $c o s ∠ A C B = \frac{4}{5}$ ，求BC的长．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象平行于直线 $y = \frac{1}{2} x$ ，且经过点 $A (2 ， 2)$ ．

(1)、求这个一次函数的表达式；

(2)、当 $x < 2$ 时，对于x的每一个值，一次函数 $y = k x + b (k \neq 0)$ 的值大于一次函数 $y = m x - 1 (m \neq 0)$ 的值，直接写出m的取值范围．

查看试题解析
23. 如图，四边形ABCD内接于 $⊙ O$ ， AB为 $⊙ O$ 的直径，点D为 $\overset{⌢}{A C}$ 的中点，对角线AC，BD交于点E， $⊙ O$ 的切线AF交BD的延长线于点F，切点为A．

(1)、求证：AE=AF；

(2)、若AF=6，BF=10，求BE的长．

查看试题解析
24. 某公园内的人工湖里有一组小型喷泉，水柱从位于湖面上方的水枪喷出，水柱落于湖面的路径形状是抛物线．现测量出如下数据，在距离水枪水平距离为d米的地点，水柱距离湖面高度为h米．
d（米）
0
0.5
2.0
3.5
5
h（米）
1.67
2. 25
3.00
2. 25
0
请解决以下问题：

(1)、在下面网格中建立适当的平面直角坐标系，根据已知数据描点，并用平滑的曲线连接；

(2)、请结合所画图象，水柱最高点距离湖面的高度是米；

(3)、求抛物线的表达式，并写出自变量的取值范围；

(4)、现有一游船宽度为2米，顶棚到湖面的高度为2.5米．要求游船从喷泉水柱中间通过时，顶棚不碰到水柱．请问游船是否能符合上述要求通过？并说明理由．

查看试题解析
25. 为了进一步加强中小学国防教育，教育部研究制定了《国防教育进中小学课程教材指南》．某中学开展了形式多样的国防教育培训活动．为了解培训效果，该校组织七、八年级全体学生参加了国防知识竞赛（百分制），并规定90分及以上为优秀，80-89分为良好，60~79分为及格，59分及以下为不及格．学校随机抽取了七、八年级各20名学生的成绩进行了整理与分析，下面给出了部分信息．
a．抽取七年级20名学生的成绩如下：
65 87 57 96 79 67 89 97 77 100
83 69 89 94 58 97 69 78 81 88
b．抽取七年级20名学生成绩的频数分布直方图如下（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）：
c．抽取八年级20名学生成绩的扇形统计图如下：
d．七年级、八年级各抽取的20名学生成绩的平均数、中位数、方差如下表：
年级
平均数
中位数
方差
七年级
81
m
167.9
八年级
82
81
108.3
请根据以上信息，回答下列问题：

(1)、补全七年级20名学生成绩的频数分布直方图，写出表中m的值；

(2)、该校目前七年级有学生300人，八年级有学生200人，估计两个年级此次测试成绩达到优秀的学生各有多少人？

(3)、你认为哪个年级的学生成绩较好，并说明理由．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，点 $(2 ， - 2)$ 在抛物线 $y = a x^{2} + b x - 2 (a < 0)$ 上．

(1)、求该抛物线的对称轴；

(2)、已知点 $(n - 2 ， y_{1})$ ， $(n - 1 ， y_{2})$ ， $(n + 1 ， y_{3})$ 在抛物线 $y = a x^{2} + b x - 2 (a < 0)$ 上．若 $0 < n < 1$ ，比较 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小，并说明理由．

查看试题解析
27. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， CD是斜边AB上的中线，EF垂直平分CD，分别交AC，BC于点E，F，连接DE，DF．

(1)、求∠EDF的度数；

(2)、用等式表示线段AE，BF，EF之间的数量关系，并证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中， $⊙ O$ 的半径为2．对于直线 $l ： y = x + 1$ 和线段BC，给出如下定义：若将线段BC沿直线l翻折可以得到 $⊙ O$ 的弦 $B^{^{'}} C^{^{'}}$ （ $B^{'}$ ， $C^{'}$ 分别是B，C的对应点），则称线段BC是以直线l为轴的 $⊙ O$ 的“关联线段”．例如：在图1中，线段BC的是以直线l为轴的 $⊙ O$ 的“关联线段”．

(1)、如图2，点 $B_{1}$ ， $C_{1}$ ， $B_{2}$ ， $C_{2}$ ， $B_{3}$ ， $C_{3}$ 的横、纵坐标都是整数．在线段 $B_{1} C_{1}$ ， $B_{2} C_{2}$ ， $B_{3} C_{3}$ 中，以直线l为轴的 $⊙ O$ 的“关联线段”是；

(2)、△ABC是边长为a的等边三角形，点 $A (0 ， 1)$ ，若BC是以直线l为轴的 $⊙ O$ 的“关联线段”，求a的值；

(3)、如果经过点 $P (- 1 ， 5)$ 的直线上存在以直线l为轴的 $⊙ O$ 的“关联线段”，直接写出这条直线与y轴交点的纵坐标m的取值范围．

查看试题解析

年级	平均数	中位数	方差
七年级	81	m	167.9
八年级	82	81	108.3

d（米）	0	0.5	2.0	3.5	5
h（米）	1.67	2. 25	3.00	2. 25	0