北京市海淀区2022年九年级下学期一模数学试卷

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是一个拱形积木玩具，其主视图是（）

A、 B、 C、 D、

查看试题解析
2. 2022年北京打造了一届绿色环保的冬奥会．张家口赛区按照“渗、滞、蓄、净、用、排”的原则，在古杨树场馆群修建了250000立方米雨水收集池，用于收集雨水和融雪水，最大限度减少水资源浪费．将250000用科学记数法表示应为（）

A、 $0.25 \times 1 0^{5}$ B、 $2.5 \times 1 0^{5}$ C、 $2.5 \times 1 0^{4}$ D、 $25 \times 1 0^{4}$

查看试题解析
3. 如图， $∠ A O B = 160 °$ ， $∠ C O B = 20 °$ ．若OD平分 $∠ A O C$ ，则 $∠ A O D$ 的大小为（）

A、20° B、70° C、80° D、140°

查看试题解析
4. 如果一个多边形的每一个外角都是 $30 °$ ，则这个多边形的边数是（）

A、6 B、8 C、10 D、12

查看试题解析
5. 不透明的袋子中装有2个红球，3个黑球，这些球除颜色外无其他差别．从袋子中随机摸出一个球，则摸出红球的概率是（）

A、 $\frac{2}{5}$ B、 $\frac{3}{5}$ C、 $\frac{2}{3}$ D、 $\frac{1}{2}$

查看试题解析
6. 实数a，b在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A、 $a < - 1$ B、 $| a | < | b |$ C、 $a + b < 0$ D、 $b - a < 0$

查看试题解析
7. 北京2022年冬奥会的开幕式上，各个国家和地区代表团入场所持的引导牌是中国结和雪花融合的造型，如图1是中国体育代表团的引导牌，观察发现，图2中的图案可以由图3中的图案经过对称、旋转等变换得到．下列关于图2和图3的说法中，错误的是（）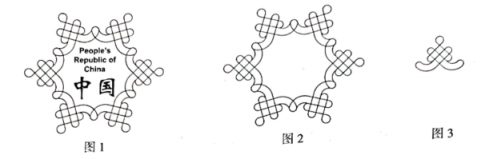

A、图2中的图案是轴对称图形 B、图2中的图案是中心对称图形 C、图2中的图案绕某个固定点旋转60°，可以与自身重合 D、将图3中的图案绕某个固定点连续旋转若干次，每次旋转120°，可以设计出图2中的图案

查看试题解析
8. 某校举办校庆晚会，其主舞台为一圆形舞台，圆心为O．A，B是舞台边缘上两个固定位置，由线段AB及优弧 $\overset{⌢}{A B}$ 围成的区域是表演区．若在A处安装一台某种型号的灯光装置，其照亮区域如图1中阴影所示．若在B处再安装一台同种型号的灯光装置，恰好可以照亮整个表演区，如图2中阴影所示．
若将灯光装置改放在如图3所示的点M，N或P处，能使表演区完全照亮的方案可能是（）
①在M处放置2台该型号的灯光装置
②在M，N处各放置1台该型号的灯光装置
③在P处放置2台该型号的灯光装置

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

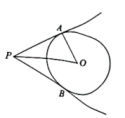
9. 若代数式 $\frac{2}{x - 3}$ 有意义，则实数x的取值范围是．

查看试题解析
10. 已知 $\sqrt{2} < m < \sqrt{11}$ ，且m是整数，请写出一个符合要求的m的值．

查看试题解析
11. 分解因式： $3 x^{2} - 3 y^{2} =$ .

查看试题解析
12. 如图，PA，PB是 $⊙ O$ 的切线，A，B为切点．若 $∠ A P B = 60 °$ ，则 $∠ A O P$ 的大小为．

查看试题解析
13. 若关于x的一元二次方程x²﹣4x+m＝0没有实数根，则m的取值范围是．

查看试题解析
14. 在平面直角坐标系 $x O y$ 中，直线 $y = a x$ 与双曲线 $y = \frac{k}{x}$ 交于点 $A (- 1 ， 2)$ 和点B，则点B的坐标为．

查看试题解析
15. 如图，在 $4 \times 4$ 的正方形网格中，A，B，C，D，E是网格线交点．请画出一个 $△ D E F$ ，使得 $△ D E F$ 与 $△ A B C$ 全等．

查看试题解析
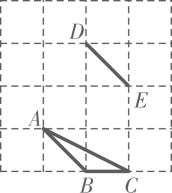16. 甲、乙在下图所示的表格中从左至右依次填数．如图，已知表中第一个数字是1，甲、乙轮流从2，3，4，5，6，7，8，9中选出一个数字填入表中（表中已出现的数字不再重复使用）．每次填数时，甲会选择填入后使表中数据方差最大的数字，乙会选择填入后使表中数据方差最小的数字．甲先填，请你在表中空白处填出一种符合要求的填数结果．
1

查看试题解析

三、解答题

17. 计算： $\sqrt{3} t a n 60 ° - \sqrt{8} + | - \sqrt{2} | - {(1 - π)}^{0}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 4 (x - 1) < 3 x ， \\ \frac{5 x + 3}{2} > x . \end{array}$

查看试题解析
19. 已知 $m^{2} - 2 m n - 3 = 0$ ，求代数式 ${(m - n)}^{2} + (m + n) (m - n) - m^{2}$ 的值．

查看试题解析
20. 《元史·天文志》中记载了元朝著名天文学家郭守敬主持的一次大规模观测，称为“四海测验”．这次观测主要使用了“立杆测影”的方法，在二十七个观测点测量出的各地的“北极出地”与现在人们所说的“北纬”完全吻合．利用类似的原理，我们也可以测量出所在地的纬度．如图1所示．
①春分时，太阳光直射赤道．此时在M地直立一根杆子MN，在太阳光照射下，杆子MN会在地面上形成影子．通过测量杆子与它的影子的长度，可以计算出太阳光与杆子MN所成的夹角 $α$ ；

②由于同一时刻的太阳光线可以近似看成是平行的，所以根据太阳光与杆子MN所成的夹角 $α$ 可以推算得到M地的纬度，即 $∠ M O B$ 的大小．

(1)、图2是①中在M地测算太阳光与杆子MN所成夹角 $α$ 的示意图．过点M作MN的垂线与直线CD交于点Q，则线段MQ可以看成是杆子MN在地面上形成的影子．使用直尺和圆规，在图2中作出影子MQ（保留作图痕迹）；

(2)、依据图1完成如下证明．
证明：∵ $A B ∥ C D$ ，

∴ $∠ M O B =$ _▲_ $= α$ （）（填推理的依据）

∴M地的纬度为 $α$ ．

查看试题解析
21. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是BC的中点，点E，F在射线AD上，且 $D E = D F$ ．

(1)、求证：四边形BECF是菱形；

(2)、若 $A D = B C = 6$ ， $A E = B E$ ，求菱形BECF的面积．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，一次函数 $y = k x + b (k \neq 0)$ 的图象由函数 $y = \frac{1}{2} x$ 的图象平移得到，且经过点 $(- 2 ， 0)$ ．

(1)、求这个一次函数的解析式；

(2)、当 $x > m$ 时，对于x的每一个值，函数 $y = 3 x - 4$ 的值大于一次函数 $y = k x + b$ 的值，直接写出m的取值范围．

查看试题解析
23. 数学学习小组的同学共同探究体积为330mL圆柱形有盖容器（如图所示）的设计方案．，他们想探究容器表面积与底面半径的关系．
具体研究过程如下，请补充完整：
⑴建立模型：设该容器的表面积为S $c m^{2}$ ，底面半径为 $x$ cm，高为 $y$ cm，则
$330 = π x^{2} y$ ，        ①
$S = 2 π x^{2} + 2 π x y$ ，        ②
由①式得 $y = \frac{330}{π x^{2}}$ ，代入②式得
$S = 2 π x^{2} + \frac{660}{x}$ ．        ③
可知，S是x的函数，自变量x的取值范围是 $x > 0$ ．
⑵探究函数：
根据函数解析式③，按照下表中自变量x的值计算（精确到个位），得到了S与x的几组对应值：
$x / c m$
…
1
1.5
2
2.5
3
3.5
4
4.5
5
5.5
6
…
$S / c m^{2}$
…
666
454
355
303
277
266
266
274
289
310
336
…
在下面平面直角坐标系中，描出了以上表中各对对应值为坐标的点．根据描出的点，画出该函数的图象；
⑶解决问题：根据图表回答，
①半径为2.4cm的圆柱形容器比半径为4.4cm的圆柱形容器表面积．（填“大”或“小”）；
②若容器的表面积为300 $c m^{2}$ ，容器底面半径约为cm（精确到0.1）．

查看试题解析
24. 如图， $⊙ O$ 是 $△ A B C$ 的外接圆，AB是 $⊙ O$ 的直径，点D为 $\overset{⌢}{A C}$ 的中点， $⊙ O$ 的切线DE交OC延长线于点E．

(1)、求证： $D E$ ；

(2)、连接BD交AC于点P，若 $A C = 8$ ， $c o s A = \frac{4}{5}$ ，求DE和BP的长．

查看试题解析
25. 为增进学生对营养与健康知识的了解，某校开展了两次知识问答活动，从中随机抽取了20名学生两次活动的成绩（百分制），并对数据（成绩）进行整理、描述和分析．下图是这20名学生第一次活动和第二次活动成绩情况统计图．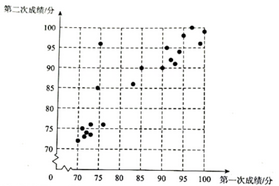

(1)、①学生甲第一次成绩是85分，则该生第二次成绩是分，他两次活动的平均成绩是分；
②学生乙第一次成绩低于80分，第二次成绩高于90分，请在图中用“○”圈出代表乙的点；

(2)、为了解每位学生两次活动平均成绩的情况，A，B，C三人分别作出了每位学生两次活动平均成绩的频数分布直方图（数据分成6组： $70 \leq x < 75$ ， $75 \leq x < 80$ ， $80 \leq x < 85$ ， $85 \leq x < 90$ ， $90 \leq x < 95$ ， $95 \leq x \leq 100$ ）：

已知这三人中只有一人符合题意作出了统计图，则作图正确的是；

(3)、假设有400名学生参加此次活动，估计两次活动平均成绩不低于90分的学生人数为．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，二次函数 $y = a x^{2} - 2 a x (a \neq 0)$ 的图象经过点 $A (- 1 ， 3)$ ．

(1)、求该二次函数的解析式以及图象顶点的坐标；

(2)、一次函数 $y = 2 x + b$ 的图象经过点A，点 $(m ， y_{1})$ 在一次函数 $y = 2 x + b$ 的图象上，点 $(m + 4 ， y_{2})$ 在二次函数 $y = a x^{2} - 2 a x$ 的图象上．若 $y_{1} > y_{2}$ ，求m的取值范围．

查看试题解析
27. 在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ B A C = 30 °$ ． D为边BC上一动点，点E在边AC上， $C E = C D$ ．点D关于点B的对称点为点F，连接AD，P为AD的中点，连接PE，PF，EF．

(1)、如图1，当点D与点B重合时，写出线段PE与PF之间的位置关系与数量关系；

(2)、如图2，当点D与点B，C不重合时，判断（1）中所得的关系是否仍然成立？若成立，请给出证明，若不成立，请举出反例．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于点 $P (x_{1} ， y_{1})$ ，给出如下定义：当点 $Q (x_{2} ， y_{2})$ 满足 $x_{1} + x_{2} = y_{1} + y_{2}$ 时，称点Q是点P的等和点．已知点 $P (2 ， 0)$ ．

(1)、在 $Q_{1} (0 ， 2)$ ， $Q_{2} (- 2 ， - 1)$ ， $Q_{3} (1 ， 3)$ 中，点P的等和点有；

(2)、点A在直线 $y = - x + 4$ 上，若点P的等和点也是点A的等和点，求点A的坐标；

(3)、已知点 $B (b ， 0)$ 和线段MN，对于所有满足 $B C = 1$ 的点C，线段MN上总存在线段PC上每个点的等和点．若MN的最小值为5，直接写出b的取值范围．

查看试题解析

$x / c m$	…	1	1.5	2	2.5	3	3.5	4	4.5	5	5.5	6	…
$S / c m^{2}$	…	666	454	355	303	277	266	266	274	289	310	336	…