安徽省宣城市宣州区狸桥片2022年中考第一次模拟数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 比﹣3小的数是( )A、0 B、1 C、﹣2 D、﹣52. 2022年1月4日上午备受瞩目的安徽G3铜陵长江公铁大桥正式动工兴建,新的一年开建的这座大桥总投资87.8亿元,其中87.8亿用科学记数法表示为( )A、 B、 C、 D、3.
图中几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 疫情期间居民为了减少外出时间,更愿意使用APP在线上购物,某购物APP今年二月份用户比一月份增加了44%,三月份用户比二月份增加了21%,求二、三两个月用户的平均每月增长率.设二、三两个月平均增长率为x,下列方程正确的是( )A、 B、 C、 D、6. 天气预报称,明天芜湖市全市的降水率为 , 下列理解正确的是( ).A、明天芜湖市全市下雨的可能性较大 B、明天芜湖市全市有的地方会下雨 C、明天芜湖市全天有的时间会下雨 D、明天芜湖市一定会下雨7. 将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2 , 抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).A、y=x2-2 B、y=-x2+2 C、y=x2+2 D、y=-x2-28. 如图,正方形ABCD一边AB在直线l上,P是直线l上点A左侧的一点,AB=2PA=4,E为边AD上一动点,过点P,E的直线与正方形ABCD的边交于点F,连接BE,BF,若设DE=x,△BEF的面积为S,则能反映S与x之间函数关系的图象是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 疫情期间居民为了减少外出时间,更愿意使用APP在线上购物,某购物APP今年二月份用户比一月份增加了44%,三月份用户比二月份增加了21%,求二、三两个月用户的平均每月增长率.设二、三两个月平均增长率为x,下列方程正确的是( )A、 B、 C、 D、6. 天气预报称,明天芜湖市全市的降水率为 , 下列理解正确的是( ).A、明天芜湖市全市下雨的可能性较大 B、明天芜湖市全市有的地方会下雨 C、明天芜湖市全天有的时间会下雨 D、明天芜湖市一定会下雨7. 将抛物线C1:y=(x-3)2+2向左平移3个单位长度,得到抛物线C2 , 抛物线C2与抛物线C3关于x轴对称,则抛物线C3的解析式为( ).A、y=x2-2 B、y=-x2+2 C、y=x2+2 D、y=-x2-28. 如图,正方形ABCD一边AB在直线l上,P是直线l上点A左侧的一点,AB=2PA=4,E为边AD上一动点,过点P,E的直线与正方形ABCD的边交于点F,连接BE,BF,若设DE=x,△BEF的面积为S,则能反映S与x之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 如图,⊙O是△ABC的外接圆, , 于点P, , 则⊙O的直径为( ).
9. 如图,⊙O是△ABC的外接圆, , 于点P, , 则⊙O的直径为( ).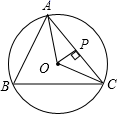 A、 B、 C、6 D、1210. 正方形的边长为8,点、分别在边、上,将正方形沿折叠,使点落在处,点落在处,交于 . 下列结论错误的是( )
A、 B、 C、6 D、1210. 正方形的边长为8,点、分别在边、上,将正方形沿折叠,使点落在处,点落在处,交于 . 下列结论错误的是( ) A、当为中点时,则 B、当时,则 C、连接 , 则 D、当(点不与、重合)在上移动时,周长随着位置变化而变化
A、当为中点时,则 B、当时,则 C、连接 , 则 D、当(点不与、重合)在上移动时,周长随着位置变化而变化二、填空题
-
11. 因式分解:12. 计算: .13. 如图,正比例函数与反比例函数的图象交于 , 两点,点C是坐标系中的一点,若 , 则OC的长为 .
 14. 如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE= , 则半圆O的直径AB是
14. 如图,AB是半圆O的直径,AC=AD,∠CAB=20°,OE⊥CD,OE= , 则半圆O的直径AB是
三、解答题
-
15. 解不等式: .16. 如图,在平面坐标内,三个顶点的坐标分别为 , , . (正方形网格中,每个小正方形的边长是1个单位长度)
 (1)、先将向下平移5个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、把绕点顺时针方向旋转后得到 , 请画出并直接写出点的坐标.17. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长.
(1)、先将向下平移5个单位长度,再向左平移3个单位长度得到 , 请画出;(2)、把绕点顺时针方向旋转后得到 , 请画出并直接写出点的坐标.17. 《九章算术》中记载了一种测量井深的方法.如图所示,在井口B处立一根垂直于井口的木杆BD,从木杆的顶端D点观察井内水岸C点,视线DC与井口的直径AB交于点E.如果测得AB=1.8米,BD=1米,BE=0.2米.请求出井深AC的长. 18. 观察以下等式:
18. 观察以下等式:第1个等式;
第2个等式;
第3个等式;
第4个等式;
……
按照以上规律,解决下列问题:
(1)、写出第5个等式: .(2)、写出你猜想的第n个等式(用含n的等式表示),并证明.19. 如图,在平面直角坐标系中,以点M(3,5)为圆心,AB为直径的圆与x轴相切,与y轴交于A,C两点,求点B的坐标.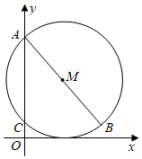 20. 2021年12月4日是第八个国家宪法日,11月29日至12月5日是第四个“宪法宣传周”,合肥某校主办了以“学习法理,弘扬法治”为主题的大赛,全校10000名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分且没有满分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)进行分组,分别为组:;组:;组:;组:;组: , 并绘制了频数分布直方图.
20. 2021年12月4日是第八个国家宪法日,11月29日至12月5日是第四个“宪法宣传周”,合肥某校主办了以“学习法理,弘扬法治”为主题的大赛,全校10000名学生都参加了此次大赛,赛后发现所有参赛学生的成绩均不低于50分且没有满分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩取整数,总分100分)进行分组,分别为组:;组:;组:;组:;组: , 并绘制了频数分布直方图. (1)、求出频数分布直方图中的值;(2)、判断这200名学生的成绩的中位数落在哪一组(直接写出结果);(3)、根据上述信息,估计全校10000名学生中成绩不低于70分的约有多少人.21. 如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,
(1)、求出频数分布直方图中的值;(2)、判断这200名学生的成绩的中位数落在哪一组(直接写出结果);(3)、根据上述信息,估计全校10000名学生中成绩不低于70分的约有多少人.21. 如图,四边形ABCD内接于⊙O, BD为直径,AC平分∠BCD,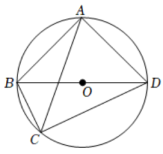 (1)、若BC=5cm,CD=12cm,求AB的长;(2)、求证:BC+CD=AC.22. 如图1所示的某种发石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将发石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系.
(1)、若BC=5cm,CD=12cm,求AB的长;(2)、求证:BC+CD=AC.22. 如图1所示的某种发石车是古代一种远程攻击的武器,发射出去的石块的运动轨迹是抛物线的一部分,且距离发射点20米时达到最大高度10米.将发石车置于山坡底部O处,山坡上有一点A,点A与点O的水平距离为30米,与地面的竖直距离为3米,AB是高度为3米的防御墙.若以点O为原点,建立如图2所示的平面直角坐标系. (1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离.23. 如图1,在△ABC中,∠BAC=90°,AB=AC,P是BC边上一点,DP⊥BC交AB边于点D,E是CD的中点,连接AE,PE.
(1)、求石块运动轨迹所在抛物线的解析式;(2)、试通过计算说明石块能否飞越防御墙AB;(3)、在竖直方向上,试求石块飞行时与坡面OA的最大距离.23. 如图1,在△ABC中,∠BAC=90°,AB=AC,P是BC边上一点,DP⊥BC交AB边于点D,E是CD的中点,连接AE,PE. (1)、线段AE与线段PE的关系为 .(2)、如图2,当点P在射线CB上,点D在射线AB上时,判断(1)中的结论是否仍然成立,并证明.(3)、如图3,点D,P分别在AB,BC边上,将△BPD绕点B顺时针旋转60°得到 , 是的中点,若 , BD=2,判断的形状并证明.
(1)、线段AE与线段PE的关系为 .(2)、如图2,当点P在射线CB上,点D在射线AB上时,判断(1)中的结论是否仍然成立,并证明.(3)、如图3,点D,P分别在AB,BC边上,将△BPD绕点B顺时针旋转60°得到 , 是的中点,若 , BD=2,判断的形状并证明.