安徽省马鞍山市2022年中考数学一模试卷
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 实数-2022是2022的( )A、绝对值 B、相反数 C、倒数 D、以上都不符合题意2. 截至2021年12月中国已向国际社会提供新冠疫苗超过18亿剂,将数据18亿用科学记数法表示为( )A、 B、 C、 D、3. 如图中,与图中几何体对应的三视图是( )
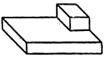 A、
A、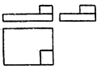 B、
B、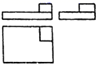 C、
C、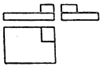 D、
D、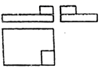 4. 一副三角板按如图所示的位置摆放,若BC∥DE,则∠1的度数是( )
4. 一副三角板按如图所示的位置摆放,若BC∥DE,则∠1的度数是( )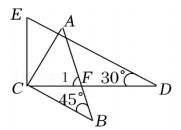 A、65° B、70° C、75° D、80°5. 已知5个正数 , , , , 的平均数是a,且 , 则数据 , , , 0, , 的平均数和中位数是( )A、 , B、 , C、 , D、 ,6. 电影《长津湖》真实生动地诠释了中国人民伟大的抗美援朝精神,一上映就受到观众的追捧,第一天票房收入2.05亿元,前三天的票房累计收入达到10.53亿元.若每天票房收入的增长率都为x,依题意可列方程( )A、2.05(1+x)=10.53 B、2.05(1+x)2=10.53 C、2.05+2.05(1+x)2=10.53 D、2.05+2.05(1+x)+2.05(1+x)2=10.537. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )
A、65° B、70° C、75° D、80°5. 已知5个正数 , , , , 的平均数是a,且 , 则数据 , , , 0, , 的平均数和中位数是( )A、 , B、 , C、 , D、 ,6. 电影《长津湖》真实生动地诠释了中国人民伟大的抗美援朝精神,一上映就受到观众的追捧,第一天票房收入2.05亿元,前三天的票房累计收入达到10.53亿元.若每天票房收入的增长率都为x,依题意可列方程( )A、2.05(1+x)=10.53 B、2.05(1+x)2=10.53 C、2.05+2.05(1+x)2=10.53 D、2.05+2.05(1+x)+2.05(1+x)2=10.537. 如图,一次函数 和反比例函数 的图象相交于 , 两点,则使 成立的 取值范围是( )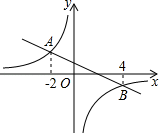 A、 或 B、 或 C、 或 D、 或8. 如图,在中, , , . 将沿着点A到点C的方向平移到的位罝,图中阴影部分面积为4,则平移的距离为( )
A、 或 B、 或 C、 或 D、 或8. 如图,在中, , , . 将沿着点A到点C的方向平移到的位罝,图中阴影部分面积为4,则平移的距离为( )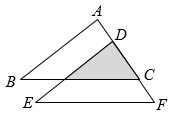 A、 B、6 C、 D、9. 如图,在中, , , E是AB的中点,过点E作AC和BC的垂线,垂足分别为点E和点F,四边形CDEF沿着CA方向匀速运动,当点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与重叠部分面积为S,则下列图象能大致反应S与t之间函数关系的是( )
A、 B、6 C、 D、9. 如图,在中, , , E是AB的中点,过点E作AC和BC的垂线,垂足分别为点E和点F,四边形CDEF沿着CA方向匀速运动,当点C与点A重合时停止运动,设运动时间为t,运动过程中四边形CDEF与重叠部分面积为S,则下列图象能大致反应S与t之间函数关系的是( )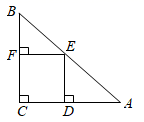 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图1,在平行四边形ABCD中, , , 动点P从点A出发,以每秒1个单位的速度沿线段AB运动到点B停止,同时动点Q从点B出发,以每秒4个单位的速度沿折线运动到点D停止.图2是点P、Q运动时,的面积S与运动时间t函数关系的图象,则a的值是( )
10. 如图1,在平行四边形ABCD中, , , 动点P从点A出发,以每秒1个单位的速度沿线段AB运动到点B停止,同时动点Q从点B出发,以每秒4个单位的速度沿折线运动到点D停止.图2是点P、Q运动时,的面积S与运动时间t函数关系的图象,则a的值是( )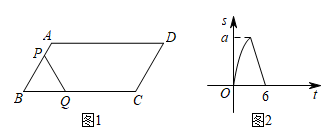 A、 B、 C、6 D、12
A、 B、 C、6 D、12二、填空题
-
11. 因式分解:.12. 如图,四边形ABCD内接于⊙O,AB是⊙O的直径,过点C作⊙O的切线交AB的延长线于点P,若∠P=40°,则∠ADC= .
 13. 不透明的盒子中装有除标号外完全相同的4个小球,小球上分别标有数-4,-2,3,5.从盒子中随机抽取一个小球,数记为a,再从剩下的球中随机抽取一个小球,数记为b,则使得点在第四象限的概率为 .14. 如图,AC垂直平分线段BD,相交于点O,且 , .
13. 不透明的盒子中装有除标号外完全相同的4个小球,小球上分别标有数-4,-2,3,5.从盒子中随机抽取一个小球,数记为a,再从剩下的球中随机抽取一个小球,数记为b,则使得点在第四象限的概率为 .14. 如图,AC垂直平分线段BD,相交于点O,且 , .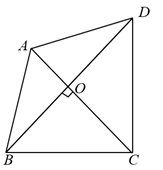 (1)、°;(2)、E为BD边上的一个动点, , 当最小时 .
(1)、°;(2)、E为BD边上的一个动点, , 当最小时 .三、解答题
-
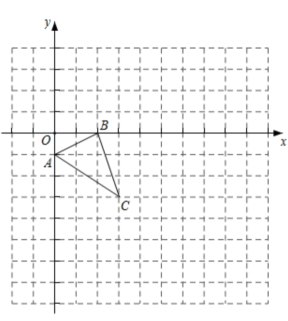
15. 计算:16. 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点(顶点是网格线的交点)及平面直角坐标系xOy.
 (1)、将绕O点逆时针旋转90°得到 , 请画出;(2)、以点O为位似中心,在第四象限将放大2倍得到 , 请画出并求的面积.17. 2022年冬奥会吉祥物冰墩墩一夜之间火遍全球,各种冰墩墩的玩偶,挂件,灯饰等应运而生.某学校决定购买A,B两种型号的冰墩墩饰品作为纪念品,已知A种比B种每件多25元,预算资金为1700元;(1)、其中800元购买A种商品,其余资金购买B种商品,且购买B种的数量是A种的3倍.求A,B两种饰品的单价.(2)、购买当日,正逢开学季搞促销,所有商品均按原价八折销售,学校调整了购买方案:在不超过预算资金的前提下,准备购买A,B两种饰品共100件;问最多购买A种商品多少件?18. 如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,的坐标为 , 的坐标为 .
(1)、将绕O点逆时针旋转90°得到 , 请画出;(2)、以点O为位似中心,在第四象限将放大2倍得到 , 请画出并求的面积.17. 2022年冬奥会吉祥物冰墩墩一夜之间火遍全球,各种冰墩墩的玩偶,挂件,灯饰等应运而生.某学校决定购买A,B两种型号的冰墩墩饰品作为纪念品,已知A种比B种每件多25元,预算资金为1700元;(1)、其中800元购买A种商品,其余资金购买B种商品,且购买B种的数量是A种的3倍.求A,B两种饰品的单价.(2)、购买当日,正逢开学季搞促销,所有商品均按原价八折销售,学校调整了购买方案:在不超过预算资金的前提下,准备购买A,B两种饰品共100件;问最多购买A种商品多少件?18. 如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,的坐标为 , 的坐标为 .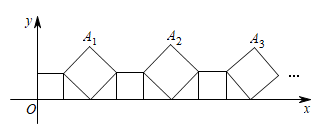 (1)、的坐标为 , 的坐标为(用含n的代数式表示);(2)、若护栏长为2020,则需要小正方形个,大正方形个.19. 如图,小明在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到D处再测得该建筑物顶点A的仰角为30°,已知山坡的坡比为1:3,BC=45米.
(1)、的坐标为 , 的坐标为(用含n的代数式表示);(2)、若护栏长为2020,则需要小正方形个,大正方形个.19. 如图,小明在山坡坡脚C处测得一座建筑物顶点A的仰角为60°,沿山坡向上走到D处再测得该建筑物顶点A的仰角为30°,已知山坡的坡比为1:3,BC=45米.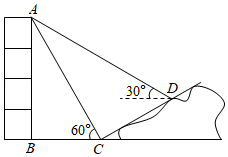 (1)、求该建筑物的高度;(结果保留根号)(2)、求小明所在位置点D的铅直高度.(结果精确到1米,参考数据≈1.414,≈1.732)20. 如图,已知AB是圆O直径,过圆上点C作 , 垂足为点D.连结OC,过点B作 , 交圆O于点E,连结AE,CE, , .
(1)、求该建筑物的高度;(结果保留根号)(2)、求小明所在位置点D的铅直高度.(结果精确到1米,参考数据≈1.414,≈1.732)20. 如图,已知AB是圆O直径,过圆上点C作 , 垂足为点D.连结OC,过点B作 , 交圆O于点E,连结AE,CE, , . (1)、求的值.(2)、求CE的长.21. 某学校组织了一次知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表.
(1)、求的值.(2)、求CE的长.21. 某学校组织了一次知识竞赛,赛后发现所有学生的成绩(总分100分)均不低于50分,为了解本次竞赛的成绩分布情况,随机抽取若干名学生的成绩作为样本进行整理,并绘制了不完整的统计图表.学校若干名学生成绩分布统计表
分数段(成绩为x分)
频数
频率
16
0.08
a
0.31
72
0.36
c
d
12
b
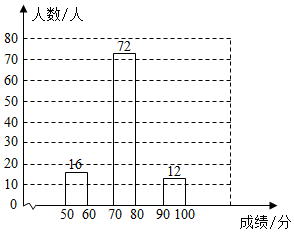
请你根据统计图表解答下列问题:
(1)、此次抽样调查的样本容量是 .(2)、填空:a= , b= , c= .(3)、请补全学生成绩分布直方图.(4)、比赛按照分数由高到低共设置一、二、三等奖,如果有25%的参赛学生能获得一等奖,那么一等奖的分数线是多少?