安徽省黄山市歙县2022年中考数学第一次模拟考试数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 2022倒数的相反数是( )A、 B、2021 C、-2021 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 据统计,截至2021年11月19日,我国加强免疫接种6573万人,为阻断新冠病毒传播、防止重症的发生等起到重要作用.其中6573万用科学记数法表示为( )A、 B、 C、 D、4. 几何体的三视图如图所示,这个几何体是( )
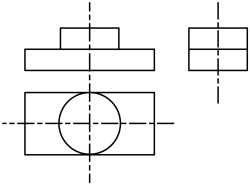 A、
A、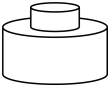 B、
B、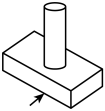 C、
C、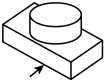 D、
D、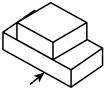 5. 某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:
5. 某中学开展“读书伴我成长”活动,为了解八年级学生四月份的读书册数,对从中随机抽取的20名学生的读书册数进行调查,结果如下表:册数/册
1
2
3
4
5
人数/人
2
5
7
4
2
根据统计表中的数据,这20名同学读书册数的众数,中位数分别是( )
A、3,3 B、3,7 C、2,7 D、7,36. 已知∠A为锐角,且cosA=0.6,那么( )A、0°<∠A<30° B、30°<∠A<45° C、45°<∠A<60° D、60°<∠A<90°7. 如图,已知AB是☉O的直径,弦AD、BC相交于P点,那么的值为( )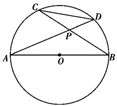 A、sin∠APC B、cos∠APC C、tan∠APC D、8. 如图,A、B是双曲线上的两个点,过点A作轴,垂足为点C,交OB于点D,若D为OB的中点,的面积为1,则k的值为( )
A、sin∠APC B、cos∠APC C、tan∠APC D、8. 如图,A、B是双曲线上的两个点,过点A作轴,垂足为点C,交OB于点D,若D为OB的中点,的面积为1,则k的值为( ) A、 B、3 C、4 D、89. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,与相交于点P,则的正弦值为( )
A、 B、3 C、4 D、89. 如图,在边长相同的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,与相交于点P,则的正弦值为( )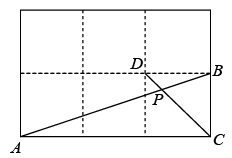 A、 B、 C、 D、10. 已知:如图,在△ABC中,于点G,于点F, , , 以下结论:① , ② , ③ , ④ , 其中正确的是( )
A、 B、 C、 D、10. 已知:如图,在△ABC中,于点G,于点F, , , 以下结论:① , ② , ③ , ④ , 其中正确的是( )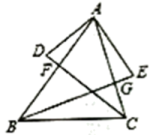 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 已知一个反比例函数的图象经过点(-2,1)和点(-1,m),则m= .12. 如图,在Rt△ABC中,∠ACB=90°点D是边AB上的一点,CD⊥AB于点D,AD=3,BD=5,则边AC的长为 .
 13. 如图,已知Rt ABC中,斜边BC上的高AD=4,cosB ,则AC=.
13. 如图,已知Rt ABC中,斜边BC上的高AD=4,cosB ,则AC=.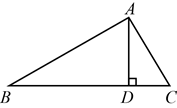 14. △ABC中,AD是BC边上的高,AD=4, , AB=8,则 .
14. △ABC中,AD是BC边上的高,AD=4, , AB=8,则 .三、解答题
-
15. 计算: .16. 观察下列等式:
第1个等式:
第2个等式:
第3个等式:
……
根据上述规律,解决下列问题:
(1)、写出第5个等式;(2)、写出你猜想的第n个等式:( )(用含n的等式表示),并证明.17. 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(1,-2)、B(4,-1)、C(3,-3).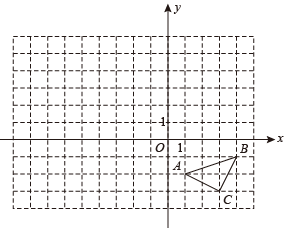
( 1 )画出将△ABC向左平移5个单位,再向上平移3个单位后的 , 并写出点B的对应点的坐标;
( 2 )以原点O为位似中心,在位似中心的同侧画出的一个位似 , 使它与的相似比为2∶1,并写出点的对应点的坐标.
18. 如图,已知反比例函数(k1>0)与一次函数相交于A、B两点,AC⊥x轴于点C. 若△OAC的面积为1,且tan∠AOC=2 .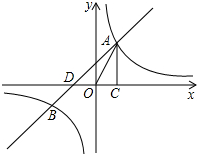 (1)、求出反比例函数与一次函数的解析式;(2)、请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.19.
(1)、求出反比例函数与一次函数的解析式;(2)、请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值大于一次函数y2的值.19.风电已成为我国继煤电、水电之后的第三大电源,风电机组主要由塔杆和叶片组成(如图1),图2是从图1引出的平面图.假设你站在A处测得塔杆顶端C的仰角是55°,沿HA方向水平前进43米到达山底G处,在山顶B处发现正好一叶片到达最高位置,此时测得叶片的顶端D(D、C、H在同一直线上)的仰角是45°.已知叶片的长度为35米(塔杆与叶片连接处的长度忽略不计),山高BG为10米,BG⊥HG,CH⊥AH,求塔杆CH的高.(参考数据:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)
 20. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
20. 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.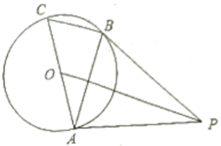 (1)、求证:PB是⊙O的切线;(2)、连接OP,若OP//BC,且OP=16,⊙O的半径为 , 求BC的长.21. 为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
(1)、求证:PB是⊙O的切线;(2)、连接OP,若OP//BC,且OP=16,⊙O的半径为 , 求BC的长.21. 为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).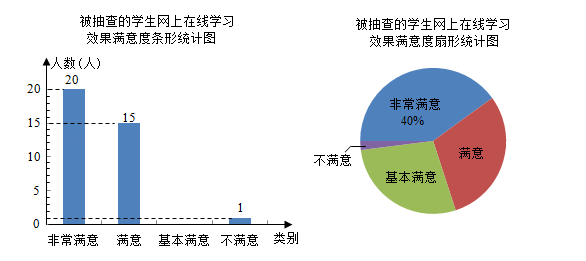
请根据图中信息解答下列问题:
(1)、求被抽查的学生人数,并补全条形统计图;(2)、求扇形统计图中表示“满意”的扇形的圆心角度数;(3)、若该校共有2000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?22. 某地草莓已经到了收获季节,已知草莓的成本价为10元/千克,投入市场销售后,发现该草莓销售不会亏本,且每天销售量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.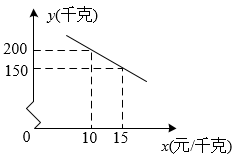 (1)、求y与x的函数关系式,并写出x的取值范围.(2)、若产量足够,当该品种的草莓定价为多少时,每天销售获得的利润最大?最大利润是多少?23. 在Rt△ABC中,∠C=90°,AC=40cm,BC=30cm.现有动点P从点A出发,沿线段AC向点C方向运动;动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是8cm/s,点Q的速度是4cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求:
(1)、求y与x的函数关系式,并写出x的取值范围.(2)、若产量足够,当该品种的草莓定价为多少时,每天销售获得的利润最大?最大利润是多少?23. 在Rt△ABC中,∠C=90°,AC=40cm,BC=30cm.现有动点P从点A出发,沿线段AC向点C方向运动;动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是8cm/s,点Q的速度是4cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动.设运动时间为t秒.求: (1)、当t=3时,P、Q两点之间的距离是多少?(2)、若△CPQ的面积为S,求S关于t的函数关系式.(3)、当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?
(1)、当t=3时,P、Q两点之间的距离是多少?(2)、若△CPQ的面积为S,求S关于t的函数关系式.(3)、当t为多少时,以点C,P,Q为顶点的三角形与△ABC相似?