天津市南开区2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 的结果等于( )A、-25 B、-35 C、6 D、-62. 的值等于( )A、 B、 C、1 D、3. 电影《长津湖》讲述了参加抗美援朝战争的志愿军战士在长津湖战役中不畏严寒、保家卫国的故事,让无数影迷感动落泪.电影获得了巨大成功,并以5770000000元取得中国电影票房冠军.其中5770000000用科学记数法表示为( )A、57.7×108 B、5.77x108 C、5.77×109 D、5.77×10104. 下列图案是历届冬奥会会徽,其中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,由8个大小相同的正方体搭成的几何体,从正面看到的形状图是( )
5. 如图,由8个大小相同的正方体搭成的几何体,从正面看到的形状图是( ) A、
A、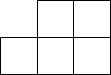 B、
B、 C、
C、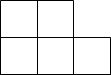 D、
D、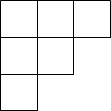 6. 设n为正整数,且 , 则n的值为( )A、7 B、8 C、9 D、107. 计算的结果为( )A、1 B、-1 C、 D、8. 方程组的解是( )A、 B、 C、 D、9. 如图,将5个大小相同的正方形置于直角坐标系中,若顶点M,N的坐标分别为(3,9),(12,9),则顶点P的坐标为( )
6. 设n为正整数,且 , 则n的值为( )A、7 B、8 C、9 D、107. 计算的结果为( )A、1 B、-1 C、 D、8. 方程组的解是( )A、 B、 C、 D、9. 如图,将5个大小相同的正方形置于直角坐标系中,若顶点M,N的坐标分别为(3,9),(12,9),则顶点P的坐标为( ) A、(13,7) B、(14,6) C、(15,5) D、(15,3)10. 已知反比例函数(a为常数)图象上三个点的坐标分别是 , 其中 , 则的大小关系的是( )A、 B、 C、 D、11. 如图,在中, , , 动点C从点О出发,沿射线OB方向移动,以AC为边向右侧作等边 , 连接BD,则下列结论不一定成立的是( )
A、(13,7) B、(14,6) C、(15,5) D、(15,3)10. 已知反比例函数(a为常数)图象上三个点的坐标分别是 , 其中 , 则的大小关系的是( )A、 B、 C、 D、11. 如图,在中, , , 动点C从点О出发,沿射线OB方向移动,以AC为边向右侧作等边 , 连接BD,则下列结论不一定成立的是( ) A、 B、 C、 D、平分12. 已知抛物线经过点 , , 对称轴在y轴右侧,则下列结论:①;②抛物线经过;③方程有两个不相等的实数根:④ . 正确的有( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、平分12. 已知抛物线经过点 , , 对称轴在y轴右侧,则下列结论:①;②抛物线经过;③方程有两个不相等的实数根:④ . 正确的有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算(﹣2a)2﹣2a2 , 结果是.14. 计算的结果是 .15. 一个不透明的布袋里装有除编号外都相同的3个球,编号分别为1、2、3.从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,则两次摸出的球的编号之和为偶数的概率是 .16. 已知一次函数的图象向上平移b个单位后经过第一象限,请你写出一个符合条件的b的值为 .17. 如图,在边长为4的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为 .

三、解答题
-
18. 如图,在每个小正方形的边长为1的网格中,的顶点A、B、C均落在格点上.
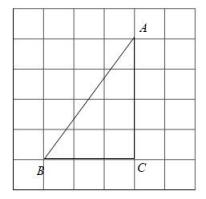 (1)、的周长为 .(2)、请在如图所示的网格中,用无刻度的直尺在AC上确定一点M,使以点M为圆心,以MC为半径的与AB相切,并简要说明点M的位置是如何找到的(不要求证明): ▲ .19. 解不等式组
(1)、的周长为 .(2)、请在如图所示的网格中,用无刻度的直尺在AC上确定一点M,使以点M为圆心,以MC为半径的与AB相切,并简要说明点M的位置是如何找到的(不要求证明): ▲ .19. 解不等式组请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: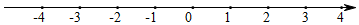 (4)、原不等式组的解集为 .20. 某校组织学生参加“希望工程”捐书活动.为了解学生所捐书本数情况,随机调查了该校的部分学生,根据调查结果,绘制了统计图①和图②.请根据相关信息,解答下列问题:
(4)、原不等式组的解集为 .20. 某校组织学生参加“希望工程”捐书活动.为了解学生所捐书本数情况,随机调查了该校的部分学生,根据调查结果,绘制了统计图①和图②.请根据相关信息,解答下列问题: (1)、本次接受调查的学生人数为 , 图①中 的值为;(2)、求统计的这组学生所捐书本数据的平均数、众数和中位数;(3)、根据统计的这组学生所捐书本数的样本数据,若该校共有 名学生,估计该校所捐书本数不低于3本的学生人数.21. 已知内接于 , 点D是上一点.
(1)、本次接受调查的学生人数为 , 图①中 的值为;(2)、求统计的这组学生所捐书本数据的平均数、众数和中位数;(3)、根据统计的这组学生所捐书本数的样本数据,若该校共有 名学生,估计该校所捐书本数不低于3本的学生人数.21. 已知内接于 , 点D是上一点. (1)、如图①,若BD为的直径,连接OD,求和的大小;(2)、如图②,若// , 连接 , 过点D作的切线,与的延长线交于点E,求的大小.22. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边 , 两点之间的距离.如图所示,小星站在湖边的处遥控无人机,无人机在处距离地面的飞行高度是 , 此时从无人机测得岸边处的俯角为 , 他抬头仰视无人机时,仰角为 , 若小星的身高 , (点 , , , 在同一平面内).
(1)、如图①,若BD为的直径,连接OD,求和的大小;(2)、如图②,若// , 连接 , 过点D作的切线,与的延长线交于点E,求的大小.22. 随着科学技术的不断进步,无人机被广泛应用到实际生活中,小星利用无人机来测量翡翠湖某处东西岸边 , 两点之间的距离.如图所示,小星站在湖边的处遥控无人机,无人机在处距离地面的飞行高度是 , 此时从无人机测得岸边处的俯角为 , 他抬头仰视无人机时,仰角为 , 若小星的身高 , (点 , , , 在同一平面内). (1)、求仰角的正弦值;(2)、求 , 两点之间的距离(结果精确到).( , , , , , )23. 甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地.甲车出发40min后乙车出发,乙车匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50km/h,结果乙车与甲车同时到达B地,甲、乙两车离A地的距离y(km)与乙车行驶时间x(h)之间的函数图象如图所示.
(1)、求仰角的正弦值;(2)、求 , 两点之间的距离(结果精确到).( , , , , , )23. 甲、乙两车从A地出发,沿同一路线驶向B地,甲车先出发匀速驶向B地.甲车出发40min后乙车出发,乙车匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50km/h,结果乙车与甲车同时到达B地,甲、乙两车离A地的距离y(km)与乙车行驶时间x(h)之间的函数图象如图所示.
请根据相关信息,解答下列问题:
(1)、图中a=;(2)、①A、B两地的距离为km;甲车行驶全程所用的时间为h;甲的速度是km/h;点C的坐标为;②直接写出线段CF对应的函数表达式;
③当乙刚到达货站时,甲距离B地还有km.
(3)、乙车出发小时在途中追上甲车;(4)、乙出发小时,甲乙两车相距50km.24. 将一个矩形OABC放置在平面直角坐标系中,点 , , 点P为BC边上的动点(点P不与点B,C重合). (1)、如图①,当时,求点P的坐标;(2)、沿OP折叠该纸片,点C的对应点为 , 设 .
(1)、如图①,当时,求点P的坐标;(2)、沿OP折叠该纸片,点C的对应点为 , 设 .①图②,若点在第四象限,与OA交于点D,试用含有t的式子表示折叠后重叠部分的面积,并直接写出t的取值范围;
②折叠后重叠部分的面积为S,当时,直接写出t的取值范围.
25. 已知抛物线(b,c为常数,)与x轴交于点 , B(点A在点B的左侧),与y轴正半轴交于点C.(1)、当时,求抛物线的顶点坐标;(2)、点P是射线OC上的一个动点①点是抛物线上的点,当 , 时,求b的值:
②若点P在线段OC上,当b的值为-4时,求的最小值.