上海市青浦区2022年九年级二模数学试题

试卷更新日期：2022-05-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ A$ 的余弦是（）

A、 $\frac{A B}{A C}$ B、 $\frac{B C}{A B}$ C、 $\frac{A C}{A B}$ D、 $\frac{A C}{B C}$

查看试题解析
2. 已知非零向量 $\vec{a}$ 和单位向量 $\vec{e}$ ，那么下列结论中，正确的是（）

A、 $| \vec{a} | = | \vec{e} | \vec{a}$ B、 $\vec{e} = \frac{1}{| \vec{a} |} \vec{a}$ C、 $\vec{a} = | \vec{e} | \vec{a}$ D、 $\vec{a} = | \vec{a} | \vec{e}$

查看试题解析
3. 下列二次根式的被开方数中，各因式指数为1的有（）

A、 $\sqrt{4 x^{2} + 9 y^{2}}$ B、 $\sqrt{5 x^{2} y}$ C、 $\sqrt{12 (x + y)}$ D、 $\sqrt{x^{2} - 2 x y + y^{2}}$

查看试题解析
4. 下列说法中，错误的有（）
①2能被6整除；②把16开平方得16的平方根，表示为 $\sqrt{16} = \pm 4$ ；③把237145精确到万位是240000；④对于实数 $a$ ，规定 $a^{\frac{n}{m}} = \sqrt[m]{a^{n}}$

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 下列关于代数式的说法中，正确的有（）
①单项式 $- 2^{2022}$ 系数是2，次数是2022次；②多项式 $\frac{x^{2}}{x} + 1$ 是一次二项；③ $\sqrt{9}$ 是二次根式；④对于实数 $a$ ， $\sqrt{a^{2}} = \pm a$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在平面直角坐标系中，已知 $A (2 ， 1)$ ， $B (0 ， 2)$ ，以 $A$ 为顶点， $B A$ 为一边作 $45 °$ 角，角的另一边交 $y$ 轴于C（C在B上方），则C坐标为（）

A、 $(0 ， 6)$ B、 $(0 ， 7)$ C、 $(0 ， \frac{22}{3})$ D、 $(0 ， \frac{13}{2})$

查看试题解析

二、填空题

7. 如果从 $π^{0}$ 、 $\frac{22}{7}$ 、-1、 $9^{\frac{1}{3}}$ 、 $t a n 30 °$ 任意选取一个数，选到的数是无理数的概率为．

查看试题解析
8. 将抛物线 $C$ 向左平移2个单位，向上平移1个单位后，所得抛物线为 $y = (x - 1)^{2}$ ，则抛物线 $C$ 解析式为．

查看试题解析
9. 抛物线y=(a−1)x²−2x+3在对称轴左侧，y随x的增大而增大，则a的取值范围是．

查看试题解析
10. 为防治新冠病毒，某医药公司一月份的产值为1亿元，若每月平均增长率为 $x$ ，第一季度的总产值为 $y$ （亿元），则 $y$ 关于 $x$ 的函数解析式为．

查看试题解析
11. 如图，是实验室里一批种子的发芽天数统计图，其中“1天发芽”的圆心角和“3天发芽”的百分比如图所示，“2天发芽”与“4天发芽”的扇形弧长相等．则这批种子的平均发芽天数为．

查看试题解析
12. 已知正多边形每个内角的度数为144°，则正多边形的边长与半径的比值为．

查看试题解析
13. 如图，已知平行四边形 $A B C D$ 中， $E$ 是 $A D$ 上一点， $E D = 2 A E$ ，联结 $B E$ 交 $A C$ 于 $F$ ，若向量 $\vec{B A} = \vec{a}$ ，向量 $\vec{B C} = \vec{b}$ ，则向量 $\vec{F A} =$ ．

查看试题解析
14. 如图，已知 $Δ A B C$ 中，点 $D$ 是 $A C$ 上一点， $D B ⊥ B C$ ，若 $∠ A D B = ∠ A B C$ ， $t a n C = \frac{1}{2}$ ，则 $\frac{A C}{A B} =$ ．

查看试题解析
15. 小明要测量公园里一棵古树的高，被一条小溪挡住去路，采用计算方法，在 $A$ 点测得古树顶的仰角为 $α$ ，向前走了100米到 $B$ 点，测得古树顶的仰角为 $β$ ，则古树的高度为米．

查看试题解析
16. 如图，已知 $Δ A B C$ 中， $D$ 、 $E$ 分别在边 $A B$ 、 $A C$ 上， $∠ A D E = ∠ C$ ， $A N$ 平分 $∠ B A C$ ，交 $D E$ 于 $M$ ，若 $S_{四边形 B C E D} = 2 S_{Δ A D E}$ ，则 $\frac{A M}{A N} =$ ．

查看试题解析
17. 如图，已知在 $Δ A B C$ 中， $A B = 13$ ， $B C = 15$ ， $s i n B = \frac{5}{13}$ ， D是边 $B C$ 上一点，将 $Δ A C D$ 沿直线AD翻折，点C落在点 $E$ 处，如果 $D E / / A B$ ，那么点E与点B的距离等于．

查看试题解析
18. 如图，在直角梯形 $A B C D$ 中， $A D$ ， $∠ A = 90 °$ ， $E$ 是 $A D$ 上一定点， $A B = 3$ ， $B C = 6$ ， $A D = 8$ ， $A E = 2$ ，点 $P$ 是 $B C$ 上一个动点，以 $P$ 为圆心， $P C$ 为半径作 $⊙ P$ ，若 $⊙ P$ 与以 $E$ 为圆心，1为半径的 $⊙ E$ 有公共点，且 $⊙ P$ 与线段 $A D$ 只有一个交点，则 $P C$ 长度的取值范围是．

查看试题解析

三、解答题

19. 先化简代数式 $\frac{x^{2} + 3 x}{x^{2} + 6 x + 9} \div \frac{x^{2} - 2 x}{x^{2} - 9}$ ，然后在下列数值 $\sqrt{2} + 4$ 、3、-3、2、0中，挑选一个作为 $x$ 的值代入求值．

查看试题解析
20. 解不等式组： ${\begin{array}{l} 2 x - 1 < \sqrt{5} x \\ \frac{x}{5} + \frac{x - 1}{3} \leq 2 \end{array}$ 并写出它的自然数解．

查看试题解析

21. 为了解某区3200名学生放学后在校体育运动的情况，调研组选择了有600名学生的

W

校，抽取40名学生进行调查，调查情况具体如下表：

图表1：感兴趣的运动项目

项目	乒乓球	篮球	足球	羽毛球	健美操
人数	4	16	10	4	6

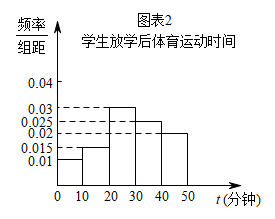(1)、此次调查的总体是，样本容量是．

(2)、若从9年级某学习加强班进行抽样调查，则这样的调查（“合适”，“不合适”），原因是样本不是样本；

(3)、根据图表1，估计该校对篮球感兴趣的学生的总人数为；

(4)、根据图表2，若从左至右依次是第一、二、三、四、五组，则中位数落在第组．

(5)、若要从对篮球感兴趣的同学中选拔出一支篮球队来，现在有以下两名学生的投篮数据，记录的是每10次投篮命中的个数．

甲同学：10、5、7、9、4；乙同学：7、8、7、6、7．若想要选择更稳定的同学，你会选择计算这两组数据的，因为这个量可以代表数据的．请计算出你所填写的统计量，并且根据计算的结果，选择合适的队员．

查看试题解析

22. 如图，已知 $A B$ 是 $⊙ O$ 的直径， $P$ 是 $A O$ 上一点，点 $C$ 、 $D$ 在直径两侧的圆周上，若 $P B$ 平分 $∠ C P D$ ，求证：劣弧 $B C$ 与劣弧 $B D$ 相等．

查看试题解析
23. 如图，已知在梯形 $A B C D$ 中， $A D / / B C$ ，对角线 $A C$ 、 $B D$ 交于 $E$ ， $B D$ 平分 $∠ A B C$ ，点 $G$ 在底边 $B C$ 上，连结 $D G$ 交对角线 $A C$ 于 $F$ ， $∠ D G B = ∠ D A B$ ．

(1)、求证：四边形 $A B G D$ 是菱形；

(2)、连结 $E G$ ，求证： $B G \cdot E G = B C \cdot E F$ ．

查看试题解析
24. 已知直线 $y = k x + b$ 经过点 $A (- 2 ， 0)$ ， $B (1 ， 3)$ 两点，抛物线 $y = a x^{2} - 4 a x + b$ 与已知直线交于C、D两点（点C在点 $D$ 的右侧），顶点为P．

(1)、求直线 $y = k x + b$ 的表达式；

(2)、若抛物线的顶点不在第一象限，求 $a$ 的取值范围；

(3)、若直线DP与直线AB所成夹角的余切值等于3，求抛物线 $y = a x^{2} - 4 a x + b$ 的表达式．

查看试题解析
25. 梯形 $A B C D$ 中， $A D$ ， $D C ⊥ B C$ 于点 $C$ ， $A B = 10$ ， $t a n B = \frac{4}{3}$ ， $⊙ O_{1}$ 以 $A B$ 为直径， $⊙ O_{2}$ 以 $C D$ 为直径，直线 $O_{1} O_{2}$ 与 $⊙ O_{1}$ 交于点 $M$ ，与 $⊙ O_{2}$ 交于点 $N$ （如图），设 $A D = x$ ．

(1)、记两圆交点为 $E$ 、 $F$ （ $E$ 在上方），当 $E F = 6$ 时，求 $x$ 的值；

(2)、当 $⊙ O_{2}$ 与线段 $A O_{1}$ 交于 $P$ 、 $Q$ 时，设 $P Q = y$ ，求 $y$ 关于 $x$ 的函数关系式，并写出定义域；

(3)、连接 $A M$ ，线段 $A M$ 与 $⊙ O_{2}$ 交于点 $G$ ，分别连接 $N G$ 、 $O_{2} G$ ，若 $Δ G M N$ 与 $Δ G N O_{2}$ 相似，求 $x$ 的值．

查看试题解析