山东省枣庄市2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. -2022的绝对值是( )A、 B、 C、2022 D、-20222. 一块含有45°的直角三角板和直尺如图放置,若∠1=55°,则∠2的度数是( )
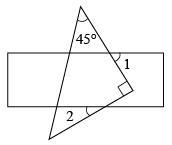 A、30° B、35° C、40° D、45°3. 下列运算正确的是( )A、 B、 C、 D、4. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A、30° B、35° C、40° D、45°3. 下列运算正确的是( )A、 B、 C、 D、4. 实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( ) A、 B、 C、 D、5. 已知 , , 且 , 则( )A、3 B、3或-3 C、1或-1 D、16. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )
A、 B、 C、 D、5. 已知 , , 且 , 则( )A、3 B、3或-3 C、1或-1 D、16. 如图,在平面直角坐标系中,四边形 为菱形, , , ,则对角线交点 的坐标为( )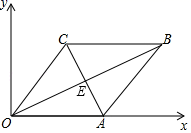 A、 B、 C、 D、7. 公元三世纪,我国汉代数学家赵爽在注解 周髀算经 时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则
A、 B、 C、 D、7. 公元三世纪,我国汉代数学家赵爽在注解 周髀算经 时给出的“赵爽弦图”如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则 A、 B、 C、 D、8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、
A、 B、 C、 D、8. 若定义一种新运算: 例如: ; .则函数 的图象大致是( )A、 B、
B、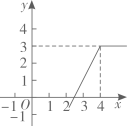 C、
C、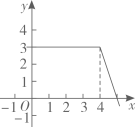 D、
D、 9. 如图,在边长为 的菱形 中, ,过点 作 于点 ,现将△ 沿直线 翻折至△ 的位置, 与 交于点 .则 等于( )
9. 如图,在边长为 的菱形 中, ,过点 作 于点 ,现将△ 沿直线 翻折至△ 的位置, 与 交于点 .则 等于( )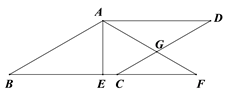 A、 B、 C、 D、10. 如图,一束光线从点出发,经轴上的点反射后经过点 , 则点的坐标是( )
A、 B、 C、 D、10. 如图,一束光线从点出发,经轴上的点反射后经过点 , 则点的坐标是( )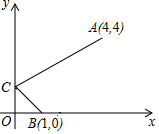 A、 B、 C、 D、11. 如图,在中,以BC为直径的半圆O交斜边AB于点D,则图中阴影部分的面积为( )
A、 B、 C、 D、11. 如图,在中,以BC为直径的半圆O交斜边AB于点D,则图中阴影部分的面积为( ) A、 B、 C、 D、12. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( )
A、 B、 C、 D、12. 二次函数 的图象如图所示,有下列结论:① ,② ,③ ,④ ,正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 若 、 满足 ,则代数式 的值为.14. 若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 .15. 如图.某大学学子餐厅把WIFI密码做成了数学题,小亮就餐时顺利地连接到了网络,那么他输入的密码是 .
 16. 如图,在 中, ,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交 于点M,N;②分别以M,N为圆心,以大于 的长为半径作弧,两弧在 内交于点O;③作射线 ,交 于点D.若点D到 的距离为1,则 的长为.
16. 如图,在 中, ,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交 于点M,N;②分别以M,N为圆心,以大于 的长为半径作弧,两弧在 内交于点O;③作射线 ,交 于点D.若点D到 的距离为1,则 的长为.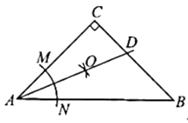 17. 把两个含 角的直角三角板按如图所示拼接在一起,点 为 的中点,连结 交 于点 .则 =.
17. 把两个含 角的直角三角板按如图所示拼接在一起,点 为 的中点,连结 交 于点 .则 =. 18. 如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点.DE、AF交于点G,AF的中点为H.连接BG、DH.给出下列结论:①;②;③;④ . 其中正确的结论是 . (请填上所有正确结论的序号)
18. 如图,在边长为4的正方形ABCD中,点E、F分别是BC、CD的中点.DE、AF交于点G,AF的中点为H.连接BG、DH.给出下列结论:①;②;③;④ . 其中正确的结论是 . (请填上所有正确结论的序号)
三、解答题
-
19. 计算: .20. 某学校为了解全校学生对电视节目(新闻、体育、动画、娱乐、戏曲)的喜爱情况,从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
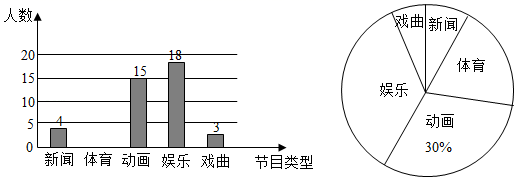
请根据以上信息,解答下列问题
(1)、这次被调查的学生共有多少名?(2)、请将条形统计图补充完整;(3)、若该校有3000名学生,估计全校学生中喜欢体育节目的约有多少名?(4)、该校宣传部需要宣传干事,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,用树状图或列表法求恰好选中甲、乙两位同学的概率.21. 如图①、图②分别是某种型号跑步机的实物图与示意图.已知跑步机手柄 与地面 平行,踏板 长为 , 与地面 的夹角 ,支架 长为 , ,求跑步机手柄 所在直线与地面 之间的距离.(结果精确到 .参考数据: , , , ) 22. 如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数的图象经过E、F两点.
22. 如图,在平面直角坐标系中,矩形OABC的两边OC、OA分别在坐标轴上,且OA=2,OC=4,连接OB.反比例函数的图象经过线段OB的中点D,并与AB、BC分别交于点E、F.一次函数的图象经过E、F两点.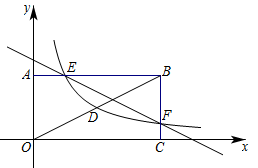 (1)、分别求出一次函数和反比例函数的表达式;(2)、点P是x轴上一动点,当PE+PF的值最小时、求点P的坐标.23. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.
(1)、分别求出一次函数和反比例函数的表达式;(2)、点P是x轴上一动点,当PE+PF的值最小时、求点P的坐标.23. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF. (1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.24. 如图, 是 的直径,点 在 上, 的平分线 交 于点 ,过点 作 ,交 的延长线于点 ,延长 、 相交于点 .
(1)、求证:四边形OEFG是矩形;(2)、若AD=10,EF=4,求OE和BG的长.24. 如图, 是 的直径,点 在 上, 的平分线 交 于点 ,过点 作 ,交 的延长线于点 ,延长 、 相交于点 . (1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.25. 如图1,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C , 已知点B坐标为(3,0),点C坐标为(0,3).
(1)、求证: 是 的切线;(2)、若 的半径为5, ,求 的长.25. 如图1,抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C , 已知点B坐标为(3,0),点C坐标为(0,3).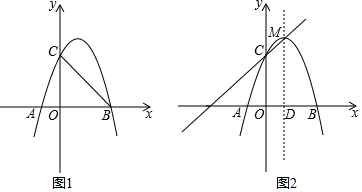 (1)、求抛物线的表达式;(2)、点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)、如图2,点M为该抛物线的顶点,直线MD⊥x轴于点D , 在直线MD上是否存在点N , 使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、点P为直线BC上方抛物线上的一个动点,当△PBC的面积最大时,求点P的坐标;(3)、如图2,点M为该抛物线的顶点,直线MD⊥x轴于点D , 在直线MD上是否存在点N , 使点N到直线MC的距离等于点N到点A的距离?若存在,求出点N的坐标;若不存在,请说明理由.