山东省青岛市李沧区2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 3的绝对值是 ( )A、-3 B、3 C、 D、2. 下列交通标志中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 新冠病毒的直径大约是0.00000008米,将0.00000008用科学记数法可表示为( )A、8×10-7 B、8×10-8 C、0.8×10-9 D、8×10-94. 某几何体的三视图如图所示,则这个几何体是( )
3. 新冠病毒的直径大约是0.00000008米,将0.00000008用科学记数法可表示为( )A、8×10-7 B、8×10-8 C、0.8×10-9 D、8×10-94. 某几何体的三视图如图所示,则这个几何体是( )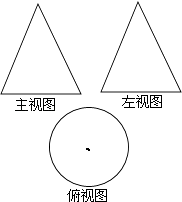 A、圆柱 B、正方体 C、球 D、圆锥5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为旋转中心,把△CDB逆时针旋转90°,则旋转后点D的对应点D′的坐标是( )
A、圆柱 B、正方体 C、球 D、圆锥5. 下列运算正确的是( )A、 B、 C、 D、6. 如图,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为旋转中心,把△CDB逆时针旋转90°,则旋转后点D的对应点D′的坐标是( )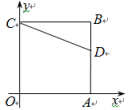 A、(-2,0) B、(2,10) C、(3,10) D、(-5,7)7. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=40°,则∠B的大小为( )
A、(-2,0) B、(2,10) C、(3,10) D、(-5,7)7. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心.若∠C=40°,则∠B的大小为( )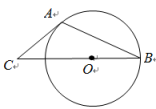 A、20° B、25° C、40° D、50°8.
A、20° B、25° C、40° D、50°8.已知二次函数y=ax2+bx+c(a , b , c是常数,且a≠0)的图象如图所示,则一次函数y=cx+ 与反比例函数 在同一坐标系内的大致图象是( )
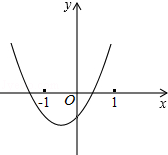 A、
A、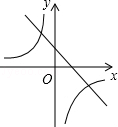 B、
B、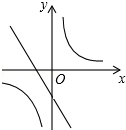 C、
C、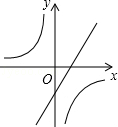 D、
D、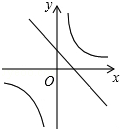
二、填空题
-
9. 某班50名同学参加了“预防溺水,珍爱生命”为主题的安全知识竞赛,竞赛成绩统计如下表,其中有两个数据被遮盖.关于成绩的三个统计量:①平均数,②方差,③众数,与被遮盖的数据无关的是 . (填写序号即可)
成绩/分
91
92
93
94
95
96
97
98
99
100
人数
■
■
1
2
3
5
6
8
10
12
10. 计算:= .11. 如图,正六边形ABCDEF的边长为9,以顶点A为圆心,AF的长为半径画圆,则图中阴影部分面积的大小为 .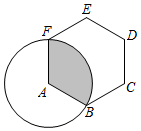 12. 对于实数x,规定表示不小于x的最小整数,例如 , , ;若 , 则x的取值范围是 .13. 如图,矩形ABCD中,AB=6,BC=8,点E是CB上的一个动点,把△DCE沿DE折叠,若点C的对应点C′刚好落在线段AB的垂直平分线上,则CE的长度为 .
12. 对于实数x,规定表示不小于x的最小整数,例如 , , ;若 , 则x的取值范围是 .13. 如图,矩形ABCD中,AB=6,BC=8,点E是CB上的一个动点,把△DCE沿DE折叠,若点C的对应点C′刚好落在线段AB的垂直平分线上,则CE的长度为 .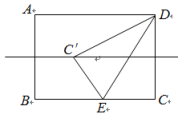 14. 如图所示,将形状、大小完全相同的“
14. 如图所示,将形状、大小完全相同的“ ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“ ”的个数为a1 , 第2幅图形中“
”的个数为a1 , 第2幅图形中“ ”的个数为a2 , 第3幅图形中“
”的个数为a2 , 第3幅图形中“ ”的个数为a3 , …,以此类推,则的值为 .
”的个数为a3 , …,以此类推,则的值为 . 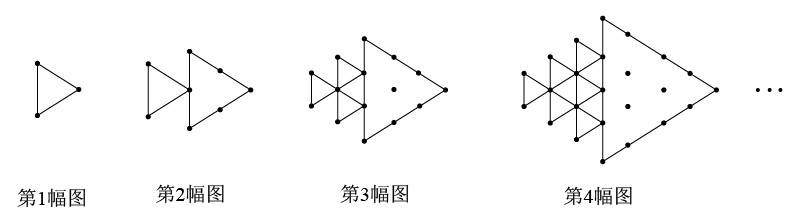
三、解答题
-
15. 已知:线段a
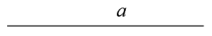
求作:等腰三角形ABC,使∠A=30°,AB=AC=a.
16.(1)、计算:;(2)、解不等式组:17. 吸烟被世界卫生组织(WHO)称为人类“第五种威胁”,为加强禁烟宣传,拒绝烟草,珍爱生命. 某校组织学生随机对部分市民就是否吸烟以及吸烟和非吸烟人群对他人在公共场所吸烟的态度(分三类:A表示主动制止,B表示反感但不制止,C表示无所谓). 进行了问卷调查,根据调查结果分别绘制了如下两个统计图. 请根据图中提供的信息解答下列问题: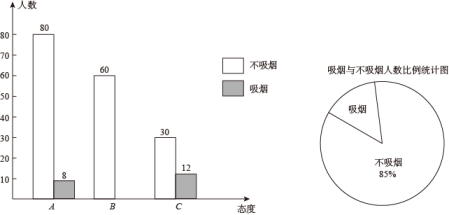 (1)、图中,“吸烟”类人数所占扇形的圆心角的度数是多少?(2)、这次被调查的市民有多少人?(3)、补全条形统计图;(4)、若该市共有市民1020万人,估计该市有多少人吸烟?18. “五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.(1)、该顾客至多可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.19. 如图是小明洗漱时的侧面示意图,洗漱台(矩形)靠墙摆放,高 , 宽 , 小明身高 , 下半身 , 洗漱时下半身与地面的夹角为 , 上半身前倾与水平面的夹角为 , 脚与洗漱台距离(点D,C,G,K在同一直线上).小明希望他的头部E恰好在洗漱盆的中点O的正上方,他应向前或后退多少cm?( , , , 结果精确到)
(1)、图中,“吸烟”类人数所占扇形的圆心角的度数是多少?(2)、这次被调查的市民有多少人?(3)、补全条形统计图;(4)、若该市共有市民1020万人,估计该市有多少人吸烟?18. “五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.(1)、该顾客至多可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.19. 如图是小明洗漱时的侧面示意图,洗漱台(矩形)靠墙摆放,高 , 宽 , 小明身高 , 下半身 , 洗漱时下半身与地面的夹角为 , 上半身前倾与水平面的夹角为 , 脚与洗漱台距离(点D,C,G,K在同一直线上).小明希望他的头部E恰好在洗漱盆的中点O的正上方,他应向前或后退多少cm?( , , , 结果精确到)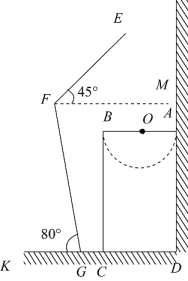 20. 为厉行节能减排,倡导绿色出行,“共享单车”登陆某市中心城区,某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批自行车包括A,B两种不同款型.请解决下列问题:(1)、该公司早期在甲街区进行了试点投放,共投放A,B两型自行车各50辆,投放成本共计20500元,其中B型车的成本单价比A型车高10元,求A,B两型自行车的成本单价各是多少?(2)、该公司决定采取如下投放方式:甲街区每1000人投放a辆“共享单车”,乙街区每1500人投放2a辆“共享单车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有12万人,试求a的值.21. 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.
20. 为厉行节能减排,倡导绿色出行,“共享单车”登陆某市中心城区,某公司拟在甲、乙两个街道社区投放一批“共享单车”,这批自行车包括A,B两种不同款型.请解决下列问题:(1)、该公司早期在甲街区进行了试点投放,共投放A,B两型自行车各50辆,投放成本共计20500元,其中B型车的成本单价比A型车高10元,求A,B两型自行车的成本单价各是多少?(2)、该公司决定采取如下投放方式:甲街区每1000人投放a辆“共享单车”,乙街区每1500人投放2a辆“共享单车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有12万人,试求a的值.21. 如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°得到△ADE,连接BD,CE交于点F.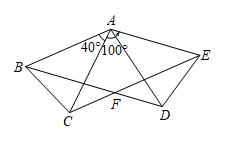 (1)、求证:△ABD ≌△ACE;(2)、试判断四边形ABFE的形状,并说明理由.22. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
(1)、求证:△ABD ≌△ACE;(2)、试判断四边形ABFE的形状,并说明理由.22. 某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.投资量x(万元)
2
种植树木利润y1(万元)
4
种植花卉利润y2(万元)
2
(1)、分别求出利润y1与y2关于投资量x的函数关系式;(2)、如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?(3)、若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.23. 问题提出我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小. 例如:
对于任意两个代数式M,N的大小比较,有下面的方法:
当M-N>0时,M >N;
当M-N=0时,M=N;
当M-N<0时,M <N.
反过来也成立. 因此,我们把这种比较两个代数式大小的方法叫做“作差法”.
对于比较两个正数a,b的大小,我们还可以用它们的平方进行比较:
∵a2-b2=(a+b)(a-b),a+b>0,
∴(a2-b2)与(a-b)的符号相同.
当a2-b2>0时,a-b>0,得a>b;
当a2-b2=0时,a-b=0,得a=b;
当a2-b2<0时,a-b<0,得a<b.
问题解决
(1)、课堂上,老师让同学们制作几种几何体,张丽同学用了3张A4纸,7张B5纸;李明同学用了2张A4纸,8张B5纸. 设每张A4纸的面积为x,每张B5纸的面积为y,且x>y,张丽同学的用纸总面积为S1 , 李明同学的用纸总面积为S2. 回答下列问题:①S1= ▲ (用含x,y的代数式表示);
S2= ▲ (用含x,y的代数式表示);
②试比较谁的用纸总面积更大?
(2)、如图1所示,要在燃气管道l上修建一个泵站,向A,B两镇供气,已知A,B到l的距离分别是3km,4km(即AC=3km,BE=4km),AB=x km,现设计两种方案: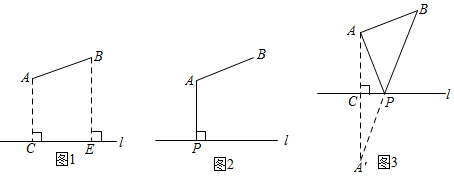
方案一:如图2所示,AP⊥l于点P,泵站修建在点P处,该方案中管道长度a1=AB+AP.
方案二:如图3所示,点A′与点A关于l对称,A′B与l相交于点P,泵站修建在点P处,该方案中管道长度a2=AP+BP.
①在方案一中,a1= ▲ km(用含x的代数式表示);
②在方案二中,a2= ▲ km(用含x的代数式表示);
③请分析说明哪种方案铺设的输气管道较短?
(3)、甲、乙两位采购员同去一家饲料公司购买两次饲料,两次购买的价格有变化,两位采购员的购货方式也不同,其中,甲每次购买1000kg,乙每次用去1000元,而不管购买多少饲料. 设两次购买的饲料单价分别为m元/kg和n元/kg(m,n是正数,且m≠n),试分析哪位采购员的购货方式合算?24. 如图,在△ABC中,AB=AC=10cm,∠B=30°.动点P从点B出发,沿BA方向运动;同时动点E从点A出发,沿AC方向运动. PF⊥BC,垂足为F,EF与PC相交于点D. 如果P,E的运动速度均为2cm/s,设运动的时间为t s(0<t<5).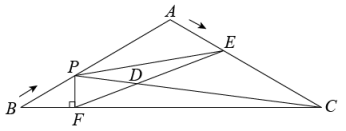 (1)、当t为何值时,PE∥BC ?(2)、设△PEF的面积为S cm2 , 求S与t的关系式;(3)、在运动过程中,是否存在某一时刻t,使△EFC与△PEF的面积比为?若存在,求出t的值,若不存在,请说明理由;(4)、当PC经过EF的中点时,求t的值.
(1)、当t为何值时,PE∥BC ?(2)、设△PEF的面积为S cm2 , 求S与t的关系式;(3)、在运动过程中,是否存在某一时刻t,使△EFC与△PEF的面积比为?若存在,求出t的值,若不存在,请说明理由;(4)、当PC经过EF的中点时,求t的值.