山东省青岛市高新区2022年九年级一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 的绝对值是( ).A、 B、 C、-3 D、2. 如图长方体的展开图,不可能是( ).
 A、
A、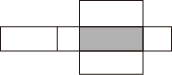 B、
B、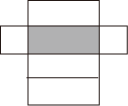 C、
C、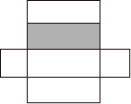 D、
D、 3. 下列图案中,既是轴对称图形又是中心对称图形是( ).A、
3. 下列图案中,既是轴对称图形又是中心对称图形是( ).A、 B、
B、 C、
C、 D、
D、 4. 在显微镜下,一种细胞的形状可以近似地看成圆,它的半径约为0.000000083m这个数据用科学记数法表示为( )A、 B、 C、 D、5. 某校篮球队12名队员的年龄情况如下:
4. 在显微镜下,一种细胞的形状可以近似地看成圆,它的半径约为0.000000083m这个数据用科学记数法表示为( )A、 B、 C、 D、5. 某校篮球队12名队员的年龄情况如下:年龄(岁)
14
15
16
17
18
人数
2
4
3
2
1
则这个队队员年龄的众数和中位数分别是( )
A、16,15 B、15,15.5 C、15,16.5 D、15,156. 如图,的顶点坐标、、 , 若绕点按逆时针方向旋转90°,再向右平移2个单位,得到,则点的对应点的坐标是( ).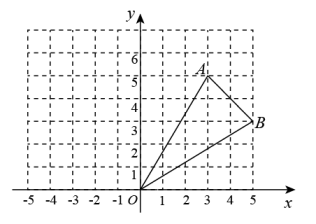 A、 B、 C、 D、7. 如图,在中, , , , 以点为圆心,以2cm的长为半径作圆,则与的位置关系是( )
A、 B、 C、 D、7. 如图,在中, , , , 以点为圆心,以2cm的长为半径作圆,则与的位置关系是( )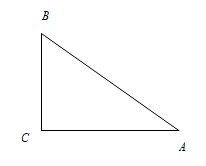 A、相离 B、相交 C、相切 D、相切或相交8. 已知,一次函数与二次函数的部分自变量与对应的函数值如表:
A、相离 B、相交 C、相切 D、相切或相交8. 已知,一次函数与二次函数的部分自变量与对应的函数值如表:…
0
2
3
4
…
…
1
3
4
5
…
…
-2
-2
4
14
…
当时,自变量的取值范围是( )
A、或 B、或 C、 D、二、填空题
-
9. 计算:.10. 在一个不透明的口袋中装有10个白球和个红球,它们除颜色外完全相同.若从中随机摸出一球;摸到红球的概率为 , 则的值为.11. 如图,A、B、C、D是半径为4cm的上的四点,AC是直径, , 则cm.
 12. 某校准备购买签字笔和笔袋奖励优秀学生,第一次购买签字笔40支,笔袋30个,购买总价为960元.第二次购买签字笔60支,笔袋50个,购买总价为1500元.每次购买签字笔和笔袋的单价都相同,求签字笔和笔袋的单价分别是多少元?若设签字笔元/支,笔袋元/个,则根据题意可列方程组为.13. 如图,在矩形中, , , 点是线段上的动点,点是线段上的动点,则的最小值是.
12. 某校准备购买签字笔和笔袋奖励优秀学生,第一次购买签字笔40支,笔袋30个,购买总价为960元.第二次购买签字笔60支,笔袋50个,购买总价为1500元.每次购买签字笔和笔袋的单价都相同,求签字笔和笔袋的单价分别是多少元?若设签字笔元/支,笔袋元/个,则根据题意可列方程组为.13. 如图,在矩形中, , , 点是线段上的动点,点是线段上的动点,则的最小值是. 14. 如图, , , P是OA上一动点(点P不与O、A重合),过点P做 , , 交OD于点B,交AD于点C,M是OP中点,N是PA中点连接BM、CN,下列结论正确的是(填写所有正确结论的序号)
14. 如图, , , P是OA上一动点(点P不与O、A重合),过点P做 , , 交OD于点B,交AD于点C,M是OP中点,N是PA中点连接BM、CN,下列结论正确的是(填写所有正确结论的序号)①是等腰三角形②③四边形是平行四边形,周长是14cm④动点无论移动到OA上哪一点(P不与O、A重合),的值为固定值是.

三、解答题
-
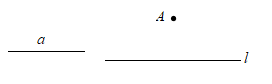
15. 已知:线段 , 直线及外一点A.
求作:菱形ABCD,使顶点A、C在直线两侧,对角线BD在直线上,且.
 16. 计算(1)、化简:(2)、解不等式组 , 并写出它的整数解.17. 2022年冬奥运会、冬残奥会不久前在北京落下帷幕,吉祥物“冰墩墩”和“雪容融”深得大家喜爱在一次活动中,奖品为一个“冰墩墩”的玩偶,小颖和小亮都想获得该奖品,组织者想到北京冬奥会2月4日开始,2月20日结束,冬残奥会3月4日开始,3月13日结束.组织者设计了一个游戏:准备A、B两组除正面数字不同其余都相同的纸牌,每组三张,A组牌正面数字分别是2,4,20.B组牌正面数字分别是3,4,13。将纸牌背面朝上,充分洗匀后,小颖从A组纸牌中摸出一张,小亮从B组纸牌中摸出一张,称为一次游戏.当摸出的两张纸牌的正面数字差的绝对值小于9,则小颖胜,否则小亮胜,获胜者即可获得“冰墩墩”的玩偶.
16. 计算(1)、化简:(2)、解不等式组 , 并写出它的整数解.17. 2022年冬奥运会、冬残奥会不久前在北京落下帷幕,吉祥物“冰墩墩”和“雪容融”深得大家喜爱在一次活动中,奖品为一个“冰墩墩”的玩偶,小颖和小亮都想获得该奖品,组织者想到北京冬奥会2月4日开始,2月20日结束,冬残奥会3月4日开始,3月13日结束.组织者设计了一个游戏:准备A、B两组除正面数字不同其余都相同的纸牌,每组三张,A组牌正面数字分别是2,4,20.B组牌正面数字分别是3,4,13。将纸牌背面朝上,充分洗匀后,小颖从A组纸牌中摸出一张,小亮从B组纸牌中摸出一张,称为一次游戏.当摸出的两张纸牌的正面数字差的绝对值小于9,则小颖胜,否则小亮胜,获胜者即可获得“冰墩墩”的玩偶.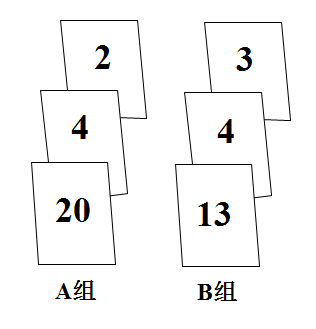 (1)、请你用列表法或画树状图求出小颖胜的概率(2)、这个游戏公平吗?请说明理由.18. 某校九年级的800名学生参加兴趣社团活动;现有以下5个兴趣社团:A.篮球社团,B.书香社团,C.舞蹈社团,D.编程社团,E.合唱社团,要求:每位学生都从中选择一个社团参加,为了了解同学们选择这5个社团的情况,现随机对九年级中的部分同学选择的兴趣社团进行了调查,收集、整理、统计、描述数据;
(1)、请你用列表法或画树状图求出小颖胜的概率(2)、这个游戏公平吗?请说明理由.18. 某校九年级的800名学生参加兴趣社团活动;现有以下5个兴趣社团:A.篮球社团,B.书香社团,C.舞蹈社团,D.编程社团,E.合唱社团,要求:每位学生都从中选择一个社团参加,为了了解同学们选择这5个社团的情况,现随机对九年级中的部分同学选择的兴趣社团进行了调查,收集、整理、统计、描述数据;选择各兴趣社团的人数统计表:
兴趣社团
人数
A.篮球社团
10
B.书香社团
8
C.舞蹈社团
a
D.编程社团
4
E.合唱社团
6
选择各兴趣社团的人数统计图:
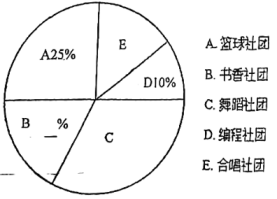
根据以上信息:
(1)、请补全统计表和统计图 , °.(2)、扇形统计图中D(编程社团)部分对应的圆心角是°;(3)、根据样本数据估计全年级选择篮球社团和合唱社团的共有多少人?19. 2022年北京冬奥会的召开惊艳世界,冬奥村的餐厅更是得到了各国运动员的好评.运动员主餐厅位于北京冬奥村居住区西南侧,共设置了世界餐台、亚洲餐台、中餐餐台、清真餐台、鲜果台、面包和甜品台等12种餐台.一送餐机器人从世界餐台A处向正南方向走200米到达亚洲餐台B处,再从B处向正东方向走500米到达中餐餐台C处,然后从C处向北偏西37°走到就餐区D处,最后从D回到A处,已知就餐区D在A的北偏东73°方向,求中餐台C到就餐区D(即CD)的距离.(结果保留整数)(参考数值: , , , , , . ) 20. 2022年疫情期问,我区爱心企业踊跃捐赠物资,以爱心助力校园抗“疫”.某爱心企业计划用2400元购买A品牌N95口罩,在购买时发现,每个A品牌N95口罩可以打八折,打折后购买的数量比打折前多100个.(1)、求打折前每个A品牌N95口罩的售价是多少元?(2)、由于学生的需求不同,该爱心企业决定购买A品牌N95口罩和B品牌N95口罩共800个.B品牌N95口罩每个原售价为7元,两种品牌N95口罩都打八折,且购买A品牌N95口罩的数量不超过总数量的一半,请问该爱心企业计划用的2400元钱是否够?如果够用,请设计一种最节省的购买方案,如果不够用,请求出至少还需要再添加多少钱?21. 已知:如图中,BD平分交AC于点D,E为AB中点,过点A作 , 交DE延长线于点F.
20. 2022年疫情期问,我区爱心企业踊跃捐赠物资,以爱心助力校园抗“疫”.某爱心企业计划用2400元购买A品牌N95口罩,在购买时发现,每个A品牌N95口罩可以打八折,打折后购买的数量比打折前多100个.(1)、求打折前每个A品牌N95口罩的售价是多少元?(2)、由于学生的需求不同,该爱心企业决定购买A品牌N95口罩和B品牌N95口罩共800个.B品牌N95口罩每个原售价为7元,两种品牌N95口罩都打八折,且购买A品牌N95口罩的数量不超过总数量的一半,请问该爱心企业计划用的2400元钱是否够?如果够用,请设计一种最节省的购买方案,如果不够用,请求出至少还需要再添加多少钱?21. 已知:如图中,BD平分交AC于点D,E为AB中点,过点A作 , 交DE延长线于点F.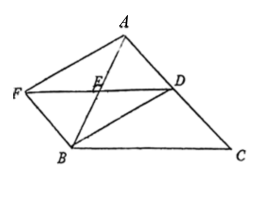 (1)、求证:(2)、当满足什么条件时,四边形AFBD是矩形?请证明你的结论.22. 2022年冬奥会在北京顺利召开,某商店购进了一批以冬奥会为主题的玩具进行销售,玩具的进价为每件30元,物价部门规定其每件的售价不低于进价且利润不高于进价的90%,根据市场调查发现,日销售量(件)与销售单价(元)的关系如图所示,在销售过程中每天还要支付其他费用共850元.
(1)、求证:(2)、当满足什么条件时,四边形AFBD是矩形?请证明你的结论.22. 2022年冬奥会在北京顺利召开,某商店购进了一批以冬奥会为主题的玩具进行销售,玩具的进价为每件30元,物价部门规定其每件的售价不低于进价且利润不高于进价的90%,根据市场调查发现,日销售量(件)与销售单价(元)的关系如图所示,在销售过程中每天还要支付其他费用共850元. (1)、求日销售量(件)与销售单价(元)的函数关系式;(2)、求该批玩具的日销售利润(元)与销售单价(元)的函数关系式;(3)、当销售单价为多少元时,该批玩具的日销售利润最大,最大利润为多少元?23. 【问题提出】计算(其中是正整数)
(1)、求日销售量(件)与销售单价(元)的函数关系式;(2)、求该批玩具的日销售利润(元)与销售单价(元)的函数关系式;(3)、当销售单价为多少元时,该批玩具的日销售利润最大,最大利润为多少元?23. 【问题提出】计算(其中是正整数)【问题探究】为解决上面的数学问题,我们可以运用数形结合的思想方法,借助图1所示的三角形,把数量关系和几何图形巧妙地结合起来进行探究.图1中,

第1行圆圈中的数为1,即;
第2行两个圆圈中数的和为2+2=2×2,
即;
第3行三个圆圈中数的和为3+3+3=3×3
即;
……;
第行个圆圈中数的和为 , 即.所有圆圈中数的和为.
要解决上面的问题,我们不妨先从特例入手:
探究一:计算.
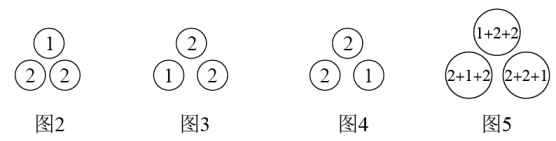
将图2按逆时针方向两次旋转得到图3、图4.观察这三个图形,可以发现同一位置圆圈的数字之和都是5(如图5),而图5共有(1+2)个这样的圆圈,因此图5中所有数字之和为5×(1+2).则图2中所有数字之和为 , 所以得到等式.
(1)、探究二:计算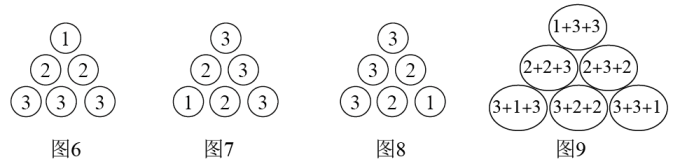
仿照上述方法,将图6按逆时针方向两次旋转得到图7、图8.观察这三个图形,可以发现同一位置圆圈的数字之和都是(如图9),而图9共有个这样的圆圈,因此图9中所有数字之和为.那么图6中所有数字之和为 , 所以得到等式.(仿照上述方法,写出探究得出的式子).
(2)、探究三:计算.(仿照上述方法,直接写出结果).(3)、【问题解决】.(仿照上述方法,直接写出探究得出的式子,用含的代数式表示)(4)、【拓广应用】计算:.(直接写出结果)
24. 已知,在菱形ABCD中,对角线AC,BD相交于点O, , .延长BC至点E,使 , 连接ED,点F从点E出发,沿ED方向向点D运动,速度为 , 过点F作垂足为点F交CE于点G;点H从点A出发,沿AD方向向点D运动,速度为 , 过点H作 , 交BD于点P,当F点停止运动时,点H也停止运动.设运动时间为 , 解答下列问题: (1)、求证:;(2)、是否存在某一时刻 , 使G点在ED的垂直平分线上?若存在,求出值;若不存在,请说明理由.(3)、设六边形PCGFDH的面积为 , 求与的函数关系式;(4)、连接HG,是否存在某一时刻 , 使?若存在,求出值;若不存在,请说明理由.
(1)、求证:;(2)、是否存在某一时刻 , 使G点在ED的垂直平分线上?若存在,求出值;若不存在,请说明理由.(3)、设六边形PCGFDH的面积为 , 求与的函数关系式;(4)、连接HG,是否存在某一时刻 , 使?若存在,求出值;若不存在,请说明理由.