山东省济宁市兖州区2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 在0,-1,-5,这四个数中,比-2小的数是( )A、0 B、-1 C、-5 D、
-
2. 如图摆放一副三角尺, ,点E在 上,点D在 的延长线上, , , ,则 ( )
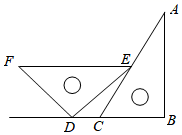 A、 B、 C、 D、
A、 B、 C、 D、 -
3. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4. 商店准备一种包装袋来包装大米,经市场调查以后,做出如下统计图,请问选择什么样的包装最合适( )
 A、 /包 B、 /包 C、 /包 D、 /包
A、 /包 B、 /包 C、 /包 D、 /包 -
5. 下列计算正确的是( )A、 B、 C、 D、
-
6. 小明15元买售价相同的软面笔记本,小丽用24元买售价相同的硬面笔记本(两人的钱恰好用完),已知每本硬面笔记本比软面笔记本贵3元,且小明和小丽买到相同数量的笔记本,设软面笔记本每本售价为x元,根据题意可列出的方程为( )
A、 B、 C、 D、 -
7. 三本相同的书叠成如图所示的几何体,它的左视图是( )
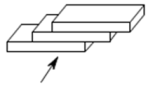 A、
A、 B、
B、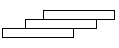 C、
C、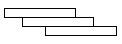 D、
D、
-
8. 把抛物线的图象向左平移1个单位,再向上平移6个单位,所得的抛物线的函数关系式是( )A、 B、 C、 D、
-
9. 构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB , 连接AD , 得∠D=15°,所以tan15° .类比这种方法,计算tan22.5°的值为( )
 A、 B、 ﹣1 C、 D、
A、 B、 ﹣1 C、 D、 -
10. 在平面直角坐标系中,如果点P的横坐标和纵坐标相等,则称点P为和谐点.例如点(1,1),(﹣ , ﹣),(﹣ , ﹣),…,都是和谐点.若二次函数y=ax2+4x+c(a≠0)的图象上有且只有一个和谐点( , ),当0≤x≤m时,函数y=ax2+4x+c﹣(a≠0)的最小值为﹣3,最大值为1,m的取值范围是( )A、m≤4 B、m≥2 C、2≤m≤4 D、2<m<4
二、填空题
-
11. 因式分解: .
-
12. 如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的倍.(精确到个位)

-
13. 某品牌鞋子的长度ycm与鞋子的“码”数x之间满足一次函数关系.若22码鞋子的长度为16cm,44码鞋子的长度为27cm,则38码鞋子的长度为cm.
-
14. 如图,AB为⊙O的直径,延长AB到点P,过点P作⊙O的切线,切点为C,连接AC,∠P=40°,D为圆上一点,则∠D的度数为 .
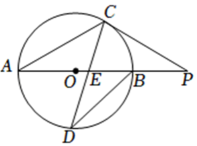
-
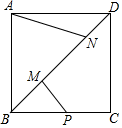
15. 如图,正方形ABCD的对角线上的两个动点M、N,满足 , 点P是BC的中点,连接AN、PM,若 , 则当的值最小时,线段AN的长度为 .
三、解答题
-
16. 计算:
-
17. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型.某校从“电脑、手机、电视、其它”四种类型的设备对学生进行了一次抽样调查,调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如图两幅不完整的统计图,请你根据图中提供的信息.解答下列问题:
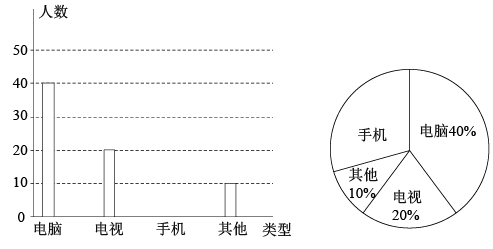 (1)、抽取的总人数是 , 在扇形统计图中,“手机”所对应的扇形的圆心角的度数为;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(4)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题.请用列表法或画树状图的方法求两次都抽取到同一名学生回答问题的概率.
(1)、抽取的总人数是 , 在扇形统计图中,“手机”所对应的扇形的圆心角的度数为;(2)、补全条形统计图;(3)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(4)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题.请用列表法或画树状图的方法求两次都抽取到同一名学生回答问题的概率. -
18. 某公司经营某种农产品,零售一箱该农产品的利润是70元,批发一箱该农产品的利润是40元.(1)、已知该公司某月卖出100箱这种农产品共获利润4600元,问:该公司当月零售、批发这种农产品的箱数分别是多少?(2)、经营性质规定,该公司零售的数量不能多于总数量的30%.现该公司要经营1000箱这种农产品,问:应如何规划零售和批发的数量,才能使总利润最大?最大总利润是多少?
-
19. 如图,点 在函数 的图像上.已知 的横坐标分别为-2、4,直线 与 轴交于点 ,连接 .
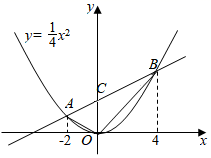 (1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图像上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个.
(1)、求直线 的函数表达式;(2)、求 的面积;(3)、若函数 的图像上存在点 ,使得 的面积等于 的面积的一半,则这样的点 共有个. -
20. 如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
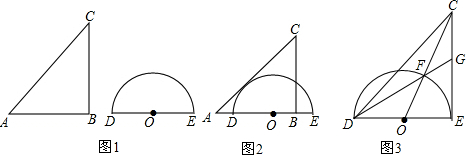 (1)、当B与O重合的时候,求三角板运动的时间;(2)、如图2,当AC与半圆相切时,求AD;(3)、如图3,当AB和DE重合时,求证:=CG·CE.
(1)、当B与O重合的时候,求三角板运动的时间;(2)、如图2,当AC与半圆相切时,求AD;(3)、如图3,当AB和DE重合时,求证:=CG·CE. -
21. 通过构造恰当的图形,可以对线段长度、图形面积大小等进行比较,直观地得到一些不等关系或最值,这是“数形结合”思想的典型应用.
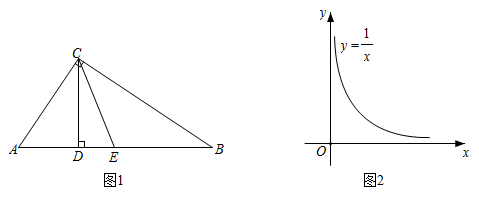 (1)、【理解】
(1)、【理解】如图1, , 垂足分别为C、D,E是的中点,连接 . 已知 , .
①分别求线段、的长(用含a、b的代数式表示);
②比较大小: ▲ (填“<”、“=”或“>”),并用含a、b的代数式表示该大小关系.
(2)、【应用】如图2,在平面直角坐标系中,点M、N在反比例函数的图像上,横坐标分别为m、n.设 , 记 .
①当时, ▲ ;当时, ▲ ;
②通过归纳猜想,可得l的最小值是 ▲ . 请利用图2构造恰当的图形,并说明你的猜想成立.
-
22. 如图,已知中, , 点P从点A出发,沿方向匀速运动,速度为;点Q从点C出发,沿方向匀速运动,速度为 , 连接并延长交的延长线于点M,过M作 , 垂足是N,设运动时间为 , 解答下列问题:
 (1)、求线段的长(用t的代数式表示);(2)、是否存在时刻t,使平分?若存在求出相应的t值,若不存在,说明理由;(3)、设四边形的面积为 , 求S与t之间的函数关系式:是否存在某一时刻t,使四边形的面积S等于面积的一半,若存在求出相应的t值,若不存在,说明理由;(4)、是否存在某一时刻t,使点A在线段的垂直平分线上,若存在求出相应的t值,若不存在,说明理由.
(1)、求线段的长(用t的代数式表示);(2)、是否存在时刻t,使平分?若存在求出相应的t值,若不存在,说明理由;(3)、设四边形的面积为 , 求S与t之间的函数关系式:是否存在某一时刻t,使四边形的面积S等于面积的一半,若存在求出相应的t值,若不存在,说明理由;(4)、是否存在某一时刻t,使点A在线段的垂直平分线上,若存在求出相应的t值,若不存在,说明理由.
