山东省东营市东营区2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、2022 B、 C、-2022 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 一把直尺和一块三角板 (含 、 角)如图所示摆放,直尺一边与三角板的两直角边分别交于点 和点 ,另一边与三角板的两直角边分别交于点 和点 ,且 ,那么 的大小为( )
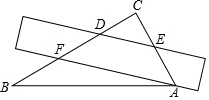 A、 B、 C、 D、4. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、
A、 B、 C、 D、4. 下列垃圾分类标识的图案既是轴对称图形,又是中心对称图形的是( )A、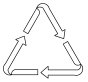 B、
B、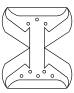 C、
C、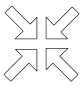 D、
D、 5. 如图,一座厂房屋顶人字架的跨度m,上弦 , . 若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
5. 如图,一座厂房屋顶人字架的跨度m,上弦 , . 若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )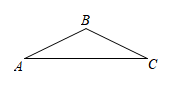 A、 B、 C、 D、6. 由于换季,商场准备对某商品打折出售,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的原售价为( )A、230元 B、250元 C、270元 D、300元7. 某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )A、 B、 C、 D、8. 如图,在Rt△ABC中, , , PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为 , 则的度数为( )
A、 B、 C、 D、6. 由于换季,商场准备对某商品打折出售,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的原售价为( )A、230元 B、250元 C、270元 D、300元7. 某学校组织学生到社区开展公益宣传活动,成立了“垃圾分类”“文明出行”“低碳环保”三个宣传队,如果小华和小丽每人随机选择参加其中一个宣传队,则她们恰好选到同一个宣传队的概率是( )A、 B、 C、 D、8. 如图,在Rt△ABC中, , , PQ垂直平分AB,垂足为Q,交BC于点P.按以下步骤作图:①以点A为圆心,以适当的长为半径作弧,分别交边AC,AB于点D,E;②分别以点D,E为圆心,以大于的长为半径作弧,两弧相交于点F;③作射线AF.若AF与PQ的夹角为 , 则的度数为( )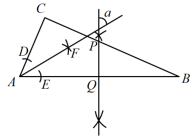 A、50° B、55° C、45° D、60°9. 如图,在Rt△ABC中, , , CD⊥AB于点D,点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F,设点P运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图像是( )
A、50° B、55° C、45° D、60°9. 如图,在Rt△ABC中, , , CD⊥AB于点D,点P从点A出发,沿A→D→C的路径运动,运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于点F,设点P运动的路程为x,四边形CEPF的面积为y,则能反映y与x之间函数关系的图像是( )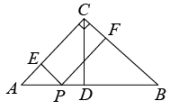 A、
A、 B、
B、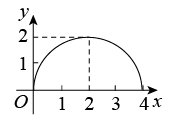 C、
C、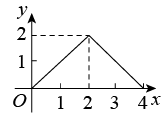 D、
D、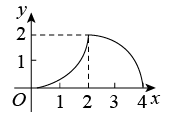 10. 如图,已知Rt△ABC, , 将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF,则下列结论中:①;②△ABD∽△ACE;③;④F为BD的中点,其中正确的有( )
10. 如图,已知Rt△ABC, , 将△ABC绕点A沿逆时针方向旋转后得到△ADE,直线BD、CE相交于点F,连接AF,则下列结论中:①;②△ABD∽△ACE;③;④F为BD的中点,其中正确的有( )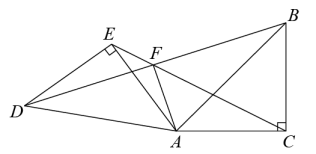 A、①②③ B、①②④ C、①②③④ D、②③④
A、①②③ B、①②④ C、①②③④ D、②③④二、填空题
-
11. 黄河在东营市垦利境内109公里,年径流量300亿立方米,正常年份,黄河每年携沙造陆3万亩左右,是中国唯一能“生长”土地的地方.则数据300亿用科学记数法表示为 .12. 分解因式: .13. 每天登录“学习强国”App进行学习,在获得积分的同时,还可获得“点点通”附加奖励,李老师最近一周每日“点点通”收入明细如表,
星期
一
二
三
四
五
六
日
收入
15
21
27
27
21
30
21
则这组数据的中位数是 .
14. 已知 , 则代数式的值等于 .15. 将点先向左平移3个单位,再向上平移2个单位,那么点的对应点的坐标是 .16. 小红用一张半径为6cm,圆心角为 的扇形纸片做成一个圆锥形的小帽子,则这个圆锥形小帽子的高为cm.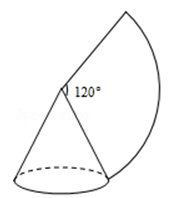 17. 如图,抛物线与x轴交于A、B两点,P是以点为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最小值是 .
17. 如图,抛物线与x轴交于A、B两点,P是以点为圆心,2为半径的圆上的动点,Q是线段PA的中点,连结OQ.则线段OQ的最小值是 .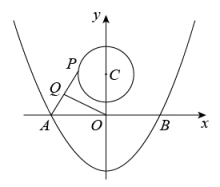 18. 如图,在平面直角坐标系中,直线与x轴交于点 , 以为边长作等边三角形 , 过点作平行于x轴,交直线l于点 , 以为边长作等边三角形 , 过点作平行于x轴,交直线l于点 , 以为边长作等边三角形 , …,则的长度为 .
18. 如图,在平面直角坐标系中,直线与x轴交于点 , 以为边长作等边三角形 , 过点作平行于x轴,交直线l于点 , 以为边长作等边三角形 , 过点作平行于x轴,交直线l于点 , 以为边长作等边三角形 , …,则的长度为 .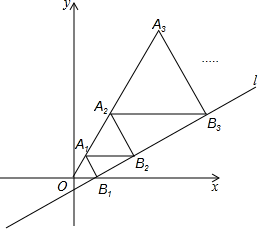
三、解答题
-
19.(1)、计算:;(2)、先化简.再求值: , 并从-2,-1,0,1中选一个合适的数作为x的值代入求值.20. 东营市某小区居民在“一针疫苗一份心,预防接种尽责任”的号召下,积极联系社区医院进行新冠疫苗接种.为了解接种进度,该小区管理人员对小区居民进行了抽样调查,按接种情况可分如下四类:A类——接种了只需要注射一针的疫苗;B类——接种了需要注射二针,且二针之间要间隔一定时间的疫苗;C类——接种了要注射三针,且每二针之间要间隔一定时间的疫苗;D类——还没有接种.图1与图2是根据此次调查得到的统计图(不完整).
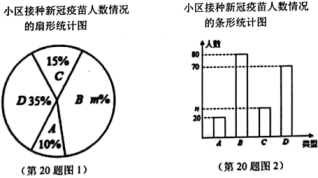
请根据统计图回答下列问题:
(1)、此次抽样调查的人数是多少人?(2)、接种B类疫苗的人数的百分比是多少?接种C类疫苗的人数是多少人?(3)、请估计该小区所居住的3000名居民中有多少人进行了新冠疫苗接种.(4)、为了继续宣传新冠疫苗接种的重要性,小区管理部门准备在已经接种疫苗的居民中征集2名志愿宣传者,现有3男2女共5名居民报名,要从这5人中随机挑选2人,求恰好抽到一男和一女的概率是多少?21. 如图,在Rt△ABC中,∠ACB=90°,点E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.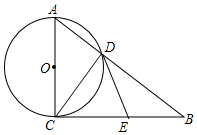 (1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若CD=6,DE=5,求⊙O的直径.22. 疫情爆发,某企业准备转型生产口罩.该企业在市场上物色到两种生产口罩的设备,若采购2台型设备,5台型设备则共需要430万元;若采购5台型设备,2台型设备则共需要550万元.已知型设备每台每天可以生产19万片口罩;型设备每台每天可以生产8万片口罩.(1)、求、两型设备的采购单价分别是多少万元/台?(2)、该企业准备采购、两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的口罩最多?每天最多可生产多少万片口罩?23. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .
(1)、判断直线DE与⊙O的位置关系,并说明理由;(2)、若CD=6,DE=5,求⊙O的直径.22. 疫情爆发,某企业准备转型生产口罩.该企业在市场上物色到两种生产口罩的设备,若采购2台型设备,5台型设备则共需要430万元;若采购5台型设备,2台型设备则共需要550万元.已知型设备每台每天可以生产19万片口罩;型设备每台每天可以生产8万片口罩.(1)、求、两型设备的采购单价分别是多少万元/台?(2)、该企业准备采购、两型设备共10台,但能用来采购设备的资金不超过700万元,那么如何安排采购方案,用这些设备每天生产的口罩最多?每天最多可生产多少万片口罩?23. 如图,已知一次函数 与反比例函数 的图象在第一、三象限分别交于 , 两点,连接 , .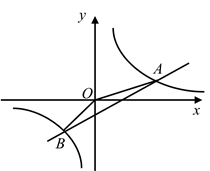 (1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.24. 如图,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,连接BC.
(1)、求一次函数和反比例函数的解析式;(2)、 的面积为;(3)、直接写出 时x的取值范围.24. 如图,已知抛物线y=ax2+bx+3与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,连接BC.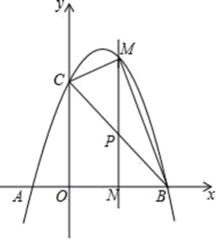 (1)、求抛物线的解析式;(2)、若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.25. 点E是矩形ABCD边AB延长线上的一动点,在矩形ABCD外作Rt△ECF,其中 , 过点F作FG⊥BC,交BC的延长线于点G,连接DF,交CG于点H.
(1)、求抛物线的解析式;(2)、若点P为线段BC上的一动点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求点P的坐标;(3)、在(2)的条件下,当△BCM的面积最大时,点D是抛物线的对称轴上的动点,在抛物线上是否存在点E,使得以A、P、D、E为顶点的四边形为平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.25. 点E是矩形ABCD边AB延长线上的一动点,在矩形ABCD外作Rt△ECF,其中 , 过点F作FG⊥BC,交BC的延长线于点G,连接DF,交CG于点H.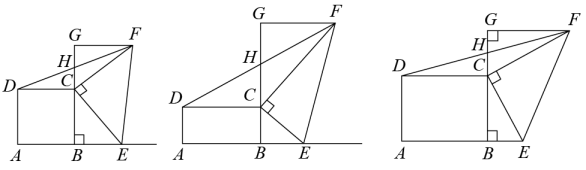 (1)、发现:如图1,若 , , 猜想线段DH与HF的数量关系是;(2)、探究:如图2,若 , , 则(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)、拓展:在(2)的基础上,若射线FC过AD的中点, , , 请你计算CE的长度.
(1)、发现:如图1,若 , , 猜想线段DH与HF的数量关系是;(2)、探究:如图2,若 , , 则(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)、拓展:在(2)的基础上,若射线FC过AD的中点, , , 请你计算CE的长度.