内蒙古呼和浩特市2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 比-3℃低5℃的温度是( )A、2℃ B、-8℃ C、-2℃ D、8℃2. 如图,点 在直线 上, .若 ,则 的大小为( )
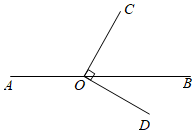 A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图是一个多功能塞子,上部是直三棱柱(其底面是等腰三角形),下部是圆柱.画出它的左视图正确的是( )
A、 B、 C、 D、3. 下列计算正确的是( )A、 B、 C、 D、4. 如图是一个多功能塞子,上部是直三棱柱(其底面是等腰三角形),下部是圆柱.画出它的左视图正确的是( ) A、
A、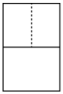 B、
B、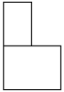 C、
C、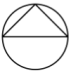 D、
D、 5. 不等式组 的解集在数轴上表示正确的是( )A、
5. 不等式组 的解集在数轴上表示正确的是( )A、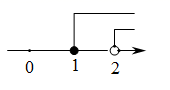 B、
B、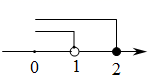 C、
C、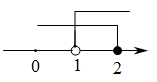 D、
D、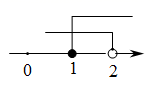 6. 半径为2的圆内接正六边形的边心距是( )A、1 B、 C、 D、7. 反比例函数图象的两支分别位于第一、三象限,则一次函数的图象大致是( )A、
6. 半径为2的圆内接正六边形的边心距是( )A、1 B、 C、 D、7. 反比例函数图象的两支分别位于第一、三象限,则一次函数的图象大致是( )A、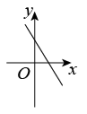 B、
B、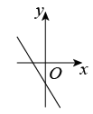 C、
C、 D、
D、 8. 以下四个命题:①直径是弦;②斜边和斜边上的中线对应相等的两个直角三角形全等;③一条弧所对的圆周角等于它所对的圆心角的一半;④数据用小数可表示为0.00124.其中真命题的个数( )A、1个 B、2个 C、3个 D、4个9. 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为( )
8. 以下四个命题:①直径是弦;②斜边和斜边上的中线对应相等的两个直角三角形全等;③一条弧所对的圆周角等于它所对的圆心角的一半;④数据用小数可表示为0.00124.其中真命题的个数( )A、1个 B、2个 C、3个 D、4个9. 在边长为2的正方形ABCD中,对角线AC与BD相交于点O,P是BD上一动点,过P作EF∥AC,分别交正方形的两条边于点E,F.设BP=x,△BEF的面积为y,则能反映y与x之间关系的图象为( )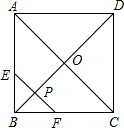 A、
A、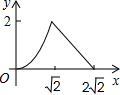 B、
B、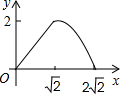 C、
C、 D、
D、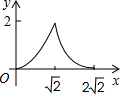
二、解答题
-
10. 2022年2月在北京市和张家口市联合举办了第24届冬季奥林匹克运动会.寒假期间学校组织部分滑雪爱好者参加冬令营集训,训练期间,每位同学都参加了40次“单板滑雪”项目训练测试.已知每次测试成绩分别为5分,4分,3分,2分,1分五档.下面是甲乙两位同学参加这个项目的40次测试成绩统计图.

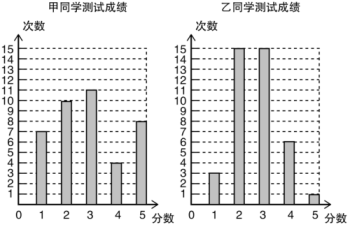
根据统计图求得的甲同学测试成绩的中位数以及对甲、乙两位同学测试成绩稳定性的判断,正确的是( )
A、3,乙更稳定 B、3,甲更稳定 C、2.5,甲更稳定 D、2.5,乙更稳定11. 计算求解(1)、计算:;(2)、解方程: .12. 疫情期间学生们居家要坚持体育锻炼,增强体质,某中学为了解学生每天体育锻炼的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.组别
时间(小时)
频数(人数)
频率
A
9
0.18
B
a
0.3
C
12
0.24
D
10
b
E
4
0.08
合计
1
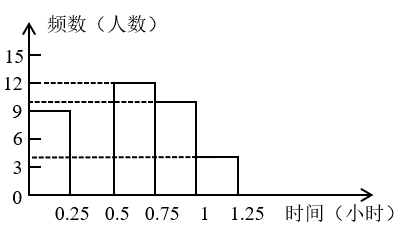
请根据图表中的信息,解答下列问题:
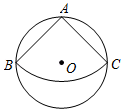
(1)、表中的a= ▲ , b= ▲ , 如果用各组的组中值代表学生每天体育锻炼的时间,则众数为 ▲ , 请补全频数分布直方图;(2)、若E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学线上分享自己享受体育锻炼所带来的快乐,请用列举法求抽取的两名学生刚好是1名男生和1名女生的概率;(3)、已知该校有2000名学生,请你依据样本数据中自己感兴趣的数据,对全校学生关于每天体育锻炼的时间情况,给出一个自己的推断,并说明推断依据.13. 如图,已知是的外接圆,AB是的直径,P是AB的延长线上的一点,弦CE交AB于点D,; . (1)、求证:PC是的切线;(2)、若 , 求弦EC所对圆周角的度数.14. 如图,一次函数的图象与反比例函数的图象相交于点、点 .
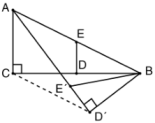
(1)、求证:PC是的切线;(2)、若 , 求弦EC所对圆周角的度数.14. 如图,一次函数的图象与反比例函数的图象相交于点、点 . (1)、求此一次函数和反比例函数的表达式;(2)、如图所示,请直接写出不等式的解集;(3)、在x轴上存在一点P,使的周长最小,直接写出点P的坐标.15. 如图,AB是一条公路旁的小山坡上树立的一块大型标语牌,标语牌底部B点到山脚C点的距离BC为20米,山坡BC的坡角为30°,某同学在山脚的平地处测量该标语牌的高度,测得C点到直立在山脚下的测角仪EF的水平距离米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°.已知A、B、D三点在同一直线上且与地面水平线DF(点C在DF上)垂直,根据测量数据求标语牌AB的高度.(结果用含非特殊角的三角函数和根号表示即可)
(1)、求此一次函数和反比例函数的表达式;(2)、如图所示,请直接写出不等式的解集;(3)、在x轴上存在一点P,使的周长最小,直接写出点P的坐标.15. 如图,AB是一条公路旁的小山坡上树立的一块大型标语牌,标语牌底部B点到山脚C点的距离BC为20米,山坡BC的坡角为30°,某同学在山脚的平地处测量该标语牌的高度,测得C点到直立在山脚下的测角仪EF的水平距离米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°.已知A、B、D三点在同一直线上且与地面水平线DF(点C在DF上)垂直,根据测量数据求标语牌AB的高度.(结果用含非特殊角的三角函数和根号表示即可)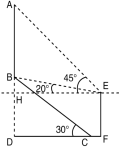 16. 某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.已知工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?17. 如图,在正方形ABCD中,点G是对角线BD上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG.
16. 某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.已知工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?17. 如图,在正方形ABCD中,点G是对角线BD上一点,CG的延长线交AB于点E,交DA的延长线于点F,连接AG. (1)、求证:;(2)、已知正方形ABCD的面积为8,G是对角线DB上靠近B的一个三等分点,求的值.18. 在平面直角坐标系xOy中, , 两点在抛物线上,记该抛物线顶点为M.(1)、若点也在该抛物线上,且 , 求该抛物线的解析式及m与n的值;(2)、已知点 , , 在该抛物线上.若 , 比较 , , , 的大小,并说明理由.
(1)、求证:;(2)、已知正方形ABCD的面积为8,G是对角线DB上靠近B的一个三等分点,求的值.18. 在平面直角坐标系xOy中, , 两点在抛物线上,记该抛物线顶点为M.(1)、若点也在该抛物线上,且 , 求该抛物线的解析式及m与n的值;(2)、已知点 , , 在该抛物线上.若 , 比较 , , , 的大小,并说明理由.三、填空题
-
19. 分解因式: .20. 从一块直径是a的圆形铁皮上剪出一个圆心角为90°的扇形,扇形的面积为 , 如果将剪下来的扇形围成一个圆锥,圆锥的底面圆直径为 .
 21. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 .
21. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的苏康码(绿码)示意图,用黑白打印机打印于边长为2cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 . 22. 在中, , , , 在直线BC上取一点P使得是等腰三角形,则可以考虑点P在线段延长线上和上的情况;当点P在线段延长线上时,等腰三角形PAB的腰长为 .
22. 在中, , , , 在直线BC上取一点P使得是等腰三角形,则可以考虑点P在线段延长线上和上的情况;当点P在线段延长线上时,等腰三角形PAB的腰长为 .