河北省石家庄市十八县2022年中考二模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 下列图形中,是直角三角形的是( )A、
 B、
B、 C、
C、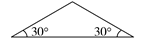 D、
D、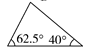 2. 在等式“(﹣6)□(﹣3)=2”中,“□”里的运算符号应是( )A、+ B、﹣ C、× D、÷3. 计算:1252-50×125+252=( )A、100 B、150 C、10000 D、225004. 已知一个几何体及其左视图如图所示,则该几何体的主视图是( )
2. 在等式“(﹣6)□(﹣3)=2”中,“□”里的运算符号应是( )A、+ B、﹣ C、× D、÷3. 计算:1252-50×125+252=( )A、100 B、150 C、10000 D、225004. 已知一个几何体及其左视图如图所示,则该几何体的主视图是( )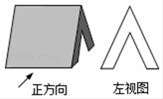 A、
A、 B、
B、 C、
C、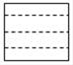 D、
D、 5. 一定相等的是( )A、a2+a2与a4 B、(a3)3与a9 C、a2﹣a2与2a2 D、a6÷a2与a36. 用科学记数法表示为a×10n的形式,则下列说法正确的是( )A、a,n都是负数 B、a是负数,n是正数 C、a,n都是正数 D、a是正数,n是负数7. 观察下列尺规作图的痕迹:
5. 一定相等的是( )A、a2+a2与a4 B、(a3)3与a9 C、a2﹣a2与2a2 D、a6÷a2与a36. 用科学记数法表示为a×10n的形式,则下列说法正确的是( )A、a,n都是负数 B、a是负数,n是正数 C、a,n都是正数 D、a是正数,n是负数7. 观察下列尺规作图的痕迹:
其中,能够说明的是( )
A、①② B、②③ C、①③ D、③④8. 某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为95分,80分,80分,若依次按照40%,25%,35%的百分比确定成绩,则该选手的成绩是( )A、86分 B、85分 C、84分 D、83分9. 如图,要判断一块纸带的两边a,b相互平行,甲、乙、丙三人的折叠与测量方案如下: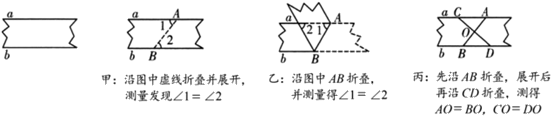
下列判断正确的是( )
A、甲、乙能得到 , 丙不能 B、甲、丙能得到 , 乙不能 C、乙、丙能得到 , 甲不能 D、甲、乙、丙均能得到10. 雪上项目占据了2022年北京冬奥会的大部分比赛项目,有自由式滑雪、越野滑雪、跳台滑雪、无舵雪橇、有舵雪橇、高山滑雪等.如图,某滑雪运动员在坡度为5:12的雪道上下滑65m,则该滑雪运动员沿竖直方向下降的高度为( ) A、13m B、25m C、m D、156 m11. 如图,在四边形ABCD中, , , AC,BD交于点O.关于四边形ABCD的形状,甲、乙、丙三人的说法如下:
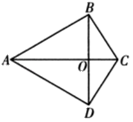
A、13m B、25m C、m D、156 m11. 如图,在四边形ABCD中, , , AC,BD交于点O.关于四边形ABCD的形状,甲、乙、丙三人的说法如下:甲:若添加“”,则四边形ABCD是菱形;
乙:若添加“”,则四边形ABCD是矩形;
丙:若添加“”,则四边形ABCD是正方形.
则说法正确的是( )
 A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙12. 如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( )
A、甲、乙 B、甲、丙 C、乙、丙 D、甲、乙、丙12. 如图(1)是两圆柱形联通容器(联通外体积忽略不计).向甲容器匀速注水,甲容器的水面高度h(cm)随时间t(分)之间的函数关系如图(2)所示,根据提供的图象信息,若甲的底面半径为1cm,则乙容器底面半径为( ) A、5cm B、4cm C、3cm D、2cm13. 如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A、5cm B、4cm C、3cm D、2cm13. 如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( ) A、6 B、12 C、24 D、4814. 要比较与中的大小(x是正数),知道的正负就可以判断,则下列说法正确的是( )A、 B、 C、 D、15. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )
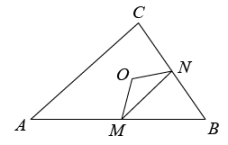
A、6 B、12 C、24 D、4814. 要比较与中的大小(x是正数),知道的正负就可以判断,则下列说法正确的是( )A、 B、 C、 D、15. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )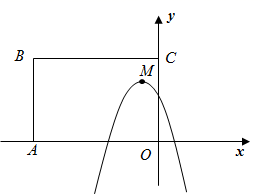 A、 B、 C、 D、16. 如图所示,点O为△ABC的内心,∠B=50°,BC<AB,点M,N分别为AB,BC上的点,且ON=OM.甲、乙、丙三位同学有如下判断:
A、 B、 C、 D、16. 如图所示,点O为△ABC的内心,∠B=50°,BC<AB,点M,N分别为AB,BC上的点,且ON=OM.甲、乙、丙三位同学有如下判断:甲:∠MON=130°;
乙:四边形OMBN的面积是逐渐变化的;
丙:当ON⊥BC时,△MON周长取得最小值.
其中正确的是( )
 A、只有甲符合题意 B、只有甲、丙符合题意 C、只有甲、乙符合题意 D、甲、乙、丙都符合题意
A、只有甲符合题意 B、只有甲、丙符合题意 C、只有甲、乙符合题意 D、甲、乙、丙都符合题意二、填空题
-
17. 若a、b互为相反数,则a+(b﹣2)的值为 ;若a、b互为倒数,则|﹣2022ab|= .18. 如图,在数轴原点O的右侧,一质点P从距原点10个单位的点A处向原点方向跳动,第一次跳动到OA的中点A1处,则点A1表示的数为 ;第二次从A1点跳动到OA1的中点A2处,第三次从A2点跳动到OA2的中点A3处,如此跳动下去,则第四次跳动后,该质点到原点O的距离为 .
 19. 如图
19. 如图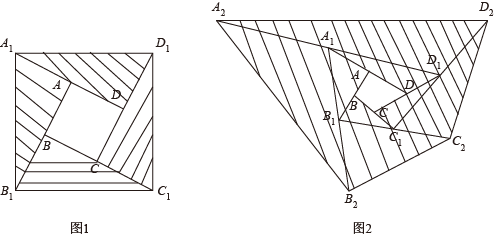 (1)、如图1,正方形ABCD的面积为a,延长边BC到点C1 , 延长边CD到点D1 , 延长边DA到点A1 , 延长边AB到点B1 , 使 , , , , 连接C1D1 , D1A1 , A1B1 , B1C1 , 得到四边形A1B1C1D1 , 此时我们称四边形ABCD向外扩展了一次,若阴影部分的面积为S1 , 则.(用含a的代数式表示)(2)、如图2,任意四边形ABCD面积为m,像(1)中那样将四边形ABCD向外进行两次扩展,第一次扩展成四边形A1B1C1D1 , 第二次扩展由四边形A1B1C1D1扩展成四边形A2B2C2D2 , 若阴影部分面积为S2 , 则.(用含m的代数式表示)
(1)、如图1,正方形ABCD的面积为a,延长边BC到点C1 , 延长边CD到点D1 , 延长边DA到点A1 , 延长边AB到点B1 , 使 , , , , 连接C1D1 , D1A1 , A1B1 , B1C1 , 得到四边形A1B1C1D1 , 此时我们称四边形ABCD向外扩展了一次,若阴影部分的面积为S1 , 则.(用含a的代数式表示)(2)、如图2,任意四边形ABCD面积为m,像(1)中那样将四边形ABCD向外进行两次扩展,第一次扩展成四边形A1B1C1D1 , 第二次扩展由四边形A1B1C1D1扩展成四边形A2B2C2D2 , 若阴影部分面积为S2 , 则.(用含m的代数式表示)三、解答题
-
20. 某校为实现垃圾分类投放,计划购进大小两种垃圾桶,大小垃圾桶的进价分别为m元/个、50元/个,购进7个大垃圾桶和10个小垃圾桶.(1)、用含m的代数式表示共付款多少元?(2)、若 , 学校预算购买垃圾桶资金为1200元是否够用?为什么?21. 按照如图所示的程序计算:
 (1)、若输入a=﹣9时,求输出结果b的值;(2)、当输入一个正数a时,输出的结果b不大于﹣11,求输入a的取值范围.22. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;
(1)、若输入a=﹣9时,求输出结果b的值;(2)、当输入一个正数a时,输出的结果b不大于﹣11,求输入a的取值范围.22. 某校七、八年级各有500名学生,为了解该校七、八年级学生对党史知识的掌握情况,从七、八年级学生中各随机抽取15人进行党史知识测试,统计这部分学生的测试成绩(成绩均为整数,满分10分,8分及以上为优秀),相关数据统计、整理如下:七年级抽取学生的成绩:6,6,6,8,8,8,8,8,8,8,9,9,9,9,10;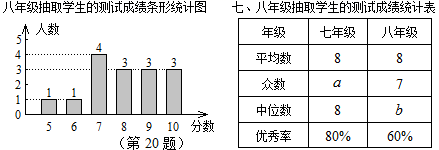 (1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.23. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点A(3,m).
(1)、填空: = , =;(2)、根据以上数据,你认为该校七、八年级中,哪个年级的学生党史知识掌握得较好?请说明理由(写出一条即可);(3)、请估计七、八年级学生对党史知识掌握能够达到优秀的总人数;(4)、现从七、八年级获得10分的4名学生中随机抽取2人参加市党史知识竞赛,请用列表或画树状图法,求出被选中的2人恰好是七、八年级各1人的概率.23. 如图,在平面直角坐标系 中,函数 的图象与直线 交于点A(3,m). (1)、求k、m的值;(2)、已知点P(n,n)(n>0),过点P作平行于 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.
(1)、求k、m的值;(2)、已知点P(n,n)(n>0),过点P作平行于 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数 的图象于点N.①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.
24. 如图,AB是半圆O的直径,D是半圆O上不同于A、B两点的任意一点,C是半圆O上一动点,AC与BD相交于点F,BE是半圆O所在圆的切线,与AC的延长线相交于点E. (1)、若AD=BC,求证:△CBA≌△DAB;(2)、若BE=BF,∠DAC=30°,AB=8.求S扇形COB;(答案保留π)(3)、若AB=8,H为AC的中点,点C从B移动到A时,请求出点H移动的长度.(答案保留π)25. 某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:
(1)、若AD=BC,求证:△CBA≌△DAB;(2)、若BE=BF,∠DAC=30°,AB=8.求S扇形COB;(答案保留π)(3)、若AB=8,H为AC的中点,点C从B移动到A时,请求出点H移动的长度.(答案保留π)25. 某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:x(天)
……
5
7
……
p(元/件)
……
248
264
……
(1)、求商品的售价p(元/件)与保存时间第x(天)之间的函数关系式;(2)、求保存第几天时,该商品不赚也不亏;(3)、请你帮助该公司确定在哪一天卖出,每件商品能获得最大利润,此时每件商品的售价是多少?26. 如图1,在矩形ABCD中,E,F,G分别为边BC,AB,AD的中点,连接DF,EF,H为DF的中点,连接GH,将△BEF绕点B旋转. (1)、当△BEF旋转到如图2所示位置,且AB=BC时,猜想GH与CE之间的关系,并证明你的猜想.(2)、已知AB=6,BC=8,
(1)、当△BEF旋转到如图2所示位置,且AB=BC时,猜想GH与CE之间的关系,并证明你的猜想.(2)、已知AB=6,BC=8,①当△BEF旋转到如图3所示位置时,猜想GH与CE之间的数量关系,并说明理由.
②射线GH,CE相交于点Q,连接BQ,在△BEF旋转过程中,BQ有最小值,请直接写出BQ的最小值.