广东省汕尾市2022年九年级二模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 16的平方根是( )A、 ±4 B、4 C、±8 D、82. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不透明的袋子中有4个白球和3个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,恰好是白球的概率为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣36. 若一次函数的图像如图所示,则下列说法正确的是( )
3. 不透明的袋子中有4个白球和3个红球,这些球除颜色外无其他差别,从袋子中随机摸出1个球,恰好是白球的概率为( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 关于x的一元二次方程x2﹣4x+3=0的解为( )A、x1=﹣1,x2=3 B、x1=1,x2=﹣3 C、x1=1,x2=3 D、x1=﹣1,x2=﹣36. 若一次函数的图像如图所示,则下列说法正确的是( )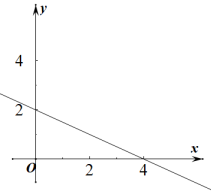 A、 B、 C、y随x的增大而增大 D、时,7. 如图,数轴上两点A,B所对应的实数分别为a,b,则的结果可能是( )
A、 B、 C、y随x的增大而增大 D、时,7. 如图,数轴上两点A,B所对应的实数分别为a,b,则的结果可能是( ) A、-1 B、0 C、2 D、8. 如图, 与 相切于点 , 交 于点 ,点 在 上,连接 、 , ,若 ,则 的度数为( )
A、-1 B、0 C、2 D、8. 如图, 与 相切于点 , 交 于点 ,点 在 上,连接 、 , ,若 ,则 的度数为( ) A、20° B、25° C、40° D、50°9. 在“探索函数的系数a,b,c与图象的关系”活动中,老师给出了直角坐标系中的四个点: , , , , 同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中a的值最大为( )
A、20° B、25° C、40° D、50°9. 在“探索函数的系数a,b,c与图象的关系”活动中,老师给出了直角坐标系中的四个点: , , , , 同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中a的值最大为( ) A、 B、 C、 D、10. 如图,将四边形纸片沿过点A的直线折叠,使得点B落在上的点M处.折痕为;再将分别沿 , 折叠,此时点C,D落在AP上的同一点N处.下面结论中正确的个数为( )
A、 B、 C、 D、10. 如图,将四边形纸片沿过点A的直线折叠,使得点B落在上的点M处.折痕为;再将分别沿 , 折叠,此时点C,D落在AP上的同一点N处.下面结论中正确的个数为( )
①M是的中点;②;③;④当时,
A、1 B、2 C、3 D、4二、填空题
-
11. 2022年“春运”期间,某市共计发送旅客约1260000人次,用科学记数法表示1260000为 .12. 计算: .13. 分解因式: .14. 一副三角板如图摆放,若AB∥CD,则的度数为 .
 15. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)
15. 如图,从楼顶 处看楼下荷塘 处的俯角为 ,看楼下荷塘 处的俯角为 ,已知楼高 为 米,则荷塘的宽 为米.(结果保留根号)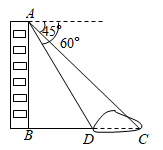 16. 如图,中, , 以点C为圆心,长为半径画弧,分别交、于点D、E,则图中阴影部分的面积为 .
16. 如图,中, , 以点C为圆心,长为半径画弧,分别交、于点D、E,则图中阴影部分的面积为 .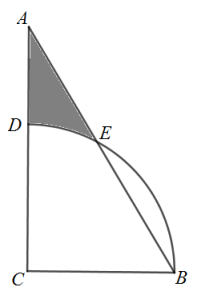 17. 如图,为等边三角形, , 点M、N分别是边、上的动点,且 , 连、交于点P,连接 , 则长度的最小值为 .
17. 如图,为等边三角形, , 点M、N分别是边、上的动点,且 , 连、交于点P,连接 , 则长度的最小值为 .
三、解答题
-
18. 先化简,再求值: ,其中 .19. 现有3个不等式;① , ② , ③ .(1)、从中任选两个不等式组成一个不等式组,并在下面横线上列出你所选的不等式组: .(2)、求出(1)中你所列不等式组的解集.20. 如图,在平行四边形 中, .(1)、在 边上确定点 ,使点 到边 , 的距离相等(用尺规作图,不写作法,保留作图痕迹);(2)、在(1)中所作的图形中,若 , ,则 .
 21. 某校为了增强学生的疫情防控意识.组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图:
21. 某校为了增强学生的疫情防控意识.组织全校2000名学生进行了疫情防控知识竞赛.从中随机抽取了n名学生的竞赛成绩(满分100分),分成四组:A: ;B: ;C: ;D: ,并绘制出如下不完整的统计图: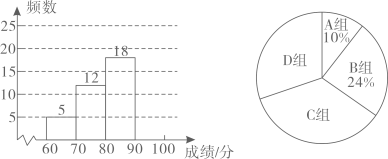 (1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.22. 今年春节期间第二十四届冬奥会在我国成功举办,吉样物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.(1)、求第一次购进的“冰墩墩”玩具每件的进价;(2)、若两次购进的“冰墩墩”玩具每件售价均为70元,且全部售完,求两次的总利润.23. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数的图象于点B,已知 .
(1)、填空:n=;(2)、补全频数分布直方图;(3)、抽取的这n名学生成绩的中位数落在组;(4)、若规定学生成绩 为优秀.估算全校成绩达到优秀的人数.22. 今年春节期间第二十四届冬奥会在我国成功举办,吉样物“冰墩墩”以其呆萌可爱、英姿飒爽形象,深受大家喜爱.某商店第一次用3000元购进一批“冰墩墩”玩具,很快售完;该商店第二次购进该“冰墩墩”玩具时,进价提高了20%,同样用3000元购进的数量比第一次少了10件.(1)、求第一次购进的“冰墩墩”玩具每件的进价;(2)、若两次购进的“冰墩墩”玩具每件售价均为70元,且全部售完,求两次的总利润.23. 如图,点在反比例函数的图象上,轴,且交y轴于点C,交反比例函数的图象于点B,已知 . (1)、求反比例函数的解析式;(2)、点D为反比例函数图象上一动点,连接交y轴于点E,当E为中点时,求的面积.24. 如图,是的直径,是的弦,M为的中点,与交于点F,过点D作 , 交的延长线于点E,且平分 .
(1)、求反比例函数的解析式;(2)、点D为反比例函数图象上一动点,连接交y轴于点E,当E为中点时,求的面积.24. 如图,是的直径,是的弦,M为的中点,与交于点F,过点D作 , 交的延长线于点E,且平分 . (1)、求证:是的切线;(2)、求证:;(3)、若 , 求BF的长.25. 如图①,抛物线 与 轴负半轴交于点 ,与 轴的另一交点为 ,与 轴正半轴交于点 ,抛物线的对称轴与直线 相交于点 ,与 轴交于点 .
(1)、求证:是的切线;(2)、求证:;(3)、若 , 求BF的长.25. 如图①,抛物线 与 轴负半轴交于点 ,与 轴的另一交点为 ,与 轴正半轴交于点 ,抛物线的对称轴与直线 相交于点 ,与 轴交于点 . (1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点 ,使得 ,利用图①求点 的坐标;(3)、如图②,抛物线的对称轴与抛物线相交于点 ,连接 ,在抛物线上是否存在点 (不与点 重合),使得 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式及对称轴;(2)、抛物线的对称轴上存在点 ,使得 ,利用图①求点 的坐标;(3)、如图②,抛物线的对称轴与抛物线相交于点 ,连接 ,在抛物线上是否存在点 (不与点 重合),使得 ?若存在,请直接写出点 的坐标;若不存在,请说明理由.