广东省佛山市南海区狮山镇2022年中考二模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
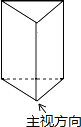
1. 的相反数是A、 B、 C、 D、2. 《长津湖之水门桥》以39.06亿元的票房创造中国电影票房的新高,将39.06亿用科学记数法表示为( ).A、39.06×109 B、3.906×109 C、390.6×1010 D、0.3906×1083. 下列计算正确的是( ).A、 B、 C、 D、4. 如图,正三棱柱的主视图为( )
 A、
A、 B、
B、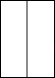 C、
C、 D、
D、 5. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )
5. 为落实“双减”政策,学校随机调查了部分学生一周平均每天的睡眠时间,统计结果如表,则这些被调查学生睡眠时间的众数和中位数分别是( )时间/小时
7
8
9
10
人数
6
9
11
4
A、9,8.5 B、9,9 C、10,9 D、11,8.56. 在同一平面直角坐标系xOy中,一次函数y=ax与二次函数y=ax2+a的图象可能是( ).A、 B、
B、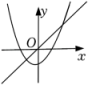 C、
C、 D、
D、 7. 若关于x的一元二次方程ax2﹣4x+2=0有两个实数根,则a的取值范围是( )A、a≤2 B、a≤2且a≠0 C、a<2 D、a<2且a≠08.
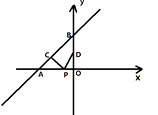
7. 若关于x的一元二次方程ax2﹣4x+2=0有两个实数根,则a的取值范围是( )A、a≤2 B、a≤2且a≠0 C、a<2 D、a<2且a≠08.直线y= x+4与x轴、y轴分别交于点A和点B , 点C , D分别为线段AB , OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( ).
 A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)9. 如图,正方形ABCD中,点E是边CD上的动点(不与点C、D重合),以CE为边向右作正方形CEFG,连接AF,点H是AF的中点,连接DH、CH.下列结论:①△ADH≌△CDH;②AF平分∠DFE;③若BC=4,CG=3,则AF=5;④若 , 则 . 其中正确的有( )
A、(-3,0) B、(-6,0) C、(- ,0) D、(- ,0)9. 如图,正方形ABCD中,点E是边CD上的动点(不与点C、D重合),以CE为边向右作正方形CEFG,连接AF,点H是AF的中点,连接DH、CH.下列结论:①△ADH≌△CDH;②AF平分∠DFE;③若BC=4,CG=3,则AF=5;④若 , 则 . 其中正确的有( )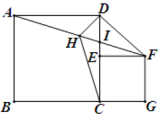 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 如图,中, , 将绕点A逆时针旋转60°得到 , 恰好经过点C,则阴影部分的面积为 .
 11. 若二次根式 有意义,则x的取值范围是 .12. 若 , 则的平方根是.13. 某人沿着坡度 的山坡起点向上走了50米,则他离地面高 米.(坡度:坡面铅直高度与水平宽度的比)14. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .
11. 若二次根式 有意义,则x的取值范围是 .12. 若 , 则的平方根是.13. 某人沿着坡度 的山坡起点向上走了50米,则他离地面高 米.(坡度:坡面铅直高度与水平宽度的比)14. 如图,在△ABC中,AD⊥BC于点D,AD与BE相交于点F,且AC=BF,DF=DC.若∠ABE=10°,则∠DBF的度数为 .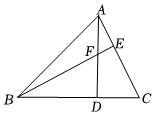 15. 如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=2.5cm,则的值为.
15. 如图,在△ABC中,AD是中线,DE⊥AB于E,DF⊥AC于F,若AB=6cm,AC=2.5cm,则的值为.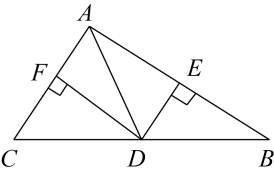 16. 已知 为实数,规定运算: , , ,……, .按以上算法计算:当 时, 的值等于.17. 如图,矩形OABC的面积为40,它的对角线OB与双曲线相交于点D,且 , 则.
16. 已知 为实数,规定运算: , , ,……, .按以上算法计算:当 时, 的值等于.17. 如图,矩形OABC的面积为40,它的对角线OB与双曲线相交于点D,且 , 则.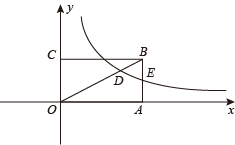
三、解答题
-
18. 先化简,再求代数式的值,其中19. 如图,AD∥BC,AD=CB.求证:E为AC中点.
 20. 如图,四边形ABCD是平行四边形.
20. 如图,四边形ABCD是平行四边形. (1)、作出∠ABC的角平分线BE,交AD于点E;(不写作法,保留作图痕迹)(2)、在(1)所作图中,若∠A=50°,求∠BED的度数.21. 某校为了解学生的运算能力,随机抽取八年级的部分学生就数学中的计算题做了测试.测试的结果分为四个等级:优秀、良好、合格、不合格;根据调查结果绘制了下列两幅不完整的统计图,请你根据以上统计图提供的信息解答以下问题:
(1)、作出∠ABC的角平分线BE,交AD于点E;(不写作法,保留作图痕迹)(2)、在(1)所作图中,若∠A=50°,求∠BED的度数.21. 某校为了解学生的运算能力,随机抽取八年级的部分学生就数学中的计算题做了测试.测试的结果分为四个等级:优秀、良好、合格、不合格;根据调查结果绘制了下列两幅不完整的统计图,请你根据以上统计图提供的信息解答以下问题: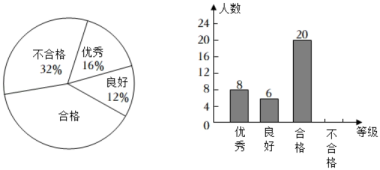 (1)、本次抽取了 ▲ 位学生,补全上面的条形统计图;(2)、若该校八年级有1600名学生,估计该校八年级运算能力为“不合格”的学生约有多少人?(3)、请你结合数据评价该校八年级学生的运算水平.22. 2022年北京冬奥会吉祥物冰墩墩和雪容融在一开售时,就深受大家的喜欢.某供应商今年2月购进一批冰墩墩和雪容融,已知一个冰墩墩的进价比一个雪容融的进价多40元,并且购买20个冰墩墩和30个雪容融的价格相同.(1)、问每个冰墩墩和雪容融的进价分别是多少元?(2)、根据市场实际,供应商计划用20000元购进这两种吉祥物200个,则他本次采购时最多可以购进多少个冰墩墩?23. 已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC= .
(1)、本次抽取了 ▲ 位学生,补全上面的条形统计图;(2)、若该校八年级有1600名学生,估计该校八年级运算能力为“不合格”的学生约有多少人?(3)、请你结合数据评价该校八年级学生的运算水平.22. 2022年北京冬奥会吉祥物冰墩墩和雪容融在一开售时,就深受大家的喜欢.某供应商今年2月购进一批冰墩墩和雪容融,已知一个冰墩墩的进价比一个雪容融的进价多40元,并且购买20个冰墩墩和30个雪容融的价格相同.(1)、问每个冰墩墩和雪容融的进价分别是多少元?(2)、根据市场实际,供应商计划用20000元购进这两种吉祥物200个,则他本次采购时最多可以购进多少个冰墩墩?23. 已知:如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数的图象交于一、三象限内的A、B两点,与x轴交于C点,点A的坐标为(2,m),点B的坐标为(n,﹣2),tan∠BOC= .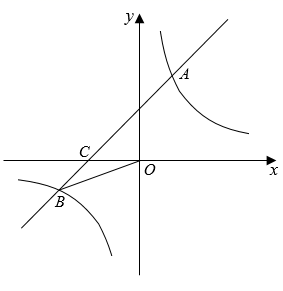 (1)、求该反比例函数和一次函数的解析式.(2)、根据图象直接写出当自变量x取何值时,一次函数值大于反比例函数值.(3)、在x轴上有一点E,使得△ABE面积是△BCO的面积4倍,求出点E的坐标.24. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接DF.
(1)、求该反比例函数和一次函数的解析式.(2)、根据图象直接写出当自变量x取何值时,一次函数值大于反比例函数值.(3)、在x轴上有一点E,使得△ABE面积是△BCO的面积4倍,求出点E的坐标.24. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接DF.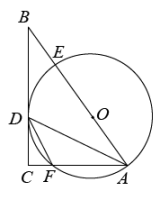 (1)、求证:BC是⊙O的切线;(2)、连接DE,求证:△BDE△BAD(3)、若BE= , sinB= , 求AD的长.25. 已知抛物线.(1)、求抛物线的对称轴;(2)、当抛物线与x轴两交点的距离是4时,求抛物线的顶点坐标;(3)、如果抛物线的图象与x轴仅有一个公共点A.过点(0,3)作直线l平行于x轴,在对称轴右侧的抛物线上任取一点P,过点P向直线l作垂线,垂足为E点,若在抛物线的对称轴上存在点D,使得△PDE是以D为直角顶点的等腰直角三角形.请求出点P的横坐标.
(1)、求证:BC是⊙O的切线;(2)、连接DE,求证:△BDE△BAD(3)、若BE= , sinB= , 求AD的长.25. 已知抛物线.(1)、求抛物线的对称轴;(2)、当抛物线与x轴两交点的距离是4时,求抛物线的顶点坐标;(3)、如果抛物线的图象与x轴仅有一个公共点A.过点(0,3)作直线l平行于x轴,在对称轴右侧的抛物线上任取一点P,过点P向直线l作垂线,垂足为E点,若在抛物线的对称轴上存在点D,使得△PDE是以D为直角顶点的等腰直角三角形.请求出点P的横坐标.