北京市房山区2022年九年级中考数学一模考试
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 如图是某几何体的三视图,该几何体是( )
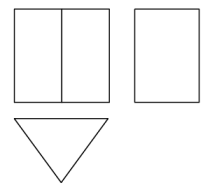 A、三棱柱 B、长方体 C、圆锥 D、圆柱2. 2021年我国加大农村义务教育薄弱环节建设力度,提高学生营养改善计划补助标准,约37000000学生受益.将37000000用科学记数法表示应为( )A、0.37×106 B、3.7×106 C、3.7×107 D、37×1063. 实数a,b,c在数轴上的对应点的位置如图所示,下列结论中正确的是( )
A、三棱柱 B、长方体 C、圆锥 D、圆柱2. 2021年我国加大农村义务教育薄弱环节建设力度,提高学生营养改善计划补助标准,约37000000学生受益.将37000000用科学记数法表示应为( )A、0.37×106 B、3.7×106 C、3.7×107 D、37×1063. 实数a,b,c在数轴上的对应点的位置如图所示,下列结论中正确的是( )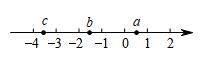 A、b-c<0 B、b>-2 C、a+c>0 D、|b|>|c|4. 下列多边形中,内角和为720°的是( )A、
A、b-c<0 B、b>-2 C、a+c>0 D、|b|>|c|4. 下列多边形中,内角和为720°的是( )A、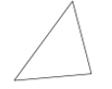 B、
B、 C、
C、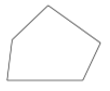 D、
D、 5. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、平行四边形 B、等腰三角形 C、正五边形 D、矩形6. 将宽为2 cm的长方形纸条折叠成如图所示的形状,那么折痕AB的长是( )
5. 下列图形中,既是中心对称图形也是轴对称图形的是( )A、平行四边形 B、等腰三角形 C、正五边形 D、矩形6. 将宽为2 cm的长方形纸条折叠成如图所示的形状,那么折痕AB的长是( )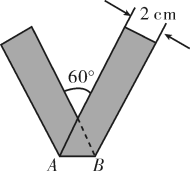 A、cm B、2cm C、4cm D、cm7. 第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )
A、cm B、2cm C、4cm D、cm7. 第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大小、质地均相同的卡片,正面分别印有高山滑雪、速度滑冰、冰球、单板滑雪、冰壶五种不同的图案,背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( ) A、 B、 C、 D、8. 某长方体木块的底面是正方形,它的高比底面边长还多50cm,把这个长方体表面涂满油漆时,如果每平方米费用为16元,那么总费用与底面边长满足的函数关系是( )A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系
A、 B、 C、 D、8. 某长方体木块的底面是正方形,它的高比底面边长还多50cm,把这个长方体表面涂满油漆时,如果每平方米费用为16元,那么总费用与底面边长满足的函数关系是( )A、正比例函数关系 B、一次函数关系 C、反比例函数关系 D、二次函数关系二、填空题
-
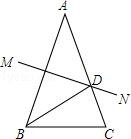
9. 若代数式 有意义,则实数x的取值范围是.10. 如图,在△ABC 中,AB=AC,AB 的垂直平分线 MN 交 AC 于 D 点.若 BD 平分∠ABC, 则∠A= .
 11. 已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是 .12. 写出一个比大且比4小的无理数 .13. 如图,点A,B,C在⊙O上,若∠OCB=20°,则∠A度数为 .
11. 已知关于x的一元二次方程有两个不相等的实数根,则a的取值范围是 .12. 写出一个比大且比4小的无理数 .13. 如图,点A,B,C在⊙O上,若∠OCB=20°,则∠A度数为 .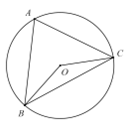 14. 已知点A(1,2),B在反比例函数的图象上,若OA=OB,则点B的坐标为 .15. 下表记录了甲、乙、丙三名射击运动员最近几次选拔赛成绩的平均数和方差:
14. 已知点A(1,2),B在反比例函数的图象上,若OA=OB,则点B的坐标为 .15. 下表记录了甲、乙、丙三名射击运动员最近几次选拔赛成绩的平均数和方差:甲
乙
丙
平均数
9.35
9.35
9.34
方差
6.6
6.9
6.7
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择 .
16. 某市为进一步加快文明城市的建设,园林局尝试种植A、B两种树种.经过试种后发现,种植A种树苗a棵,种下后成活了棵,种植B种树苗b棵,种下后成活了(b-2)棵.第一阶段两种树苗共种植40棵,且两种树苗的成活棵树相同,则种植A种树苗棵.第二阶段,该园林局又种植A种树苗m棵,B种树苗n棵,若m=2n,在第一阶段的基础上进行统计,则这两个阶段种植A种树苗成活棵数种植B种树苗成活棵数(填“>”“<”或“=”).三、解答题
-
17. 计算: .18. 解不等式组:19. 已知 , 求代数式的值.20. 已知:如图,点M为锐角∠APB 的边PA上一点.
求作:∠AMD,使得点D在边PB上,且∠AMD =2∠P.
作法:
①以点M为圆心,MP长为半径画圆,交PA于另一点C,交PB于点D点;
②作射线MD.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹);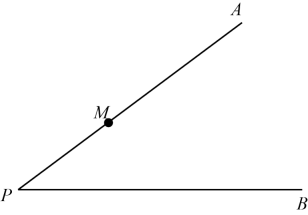 (2)、完成下面的证明.
(2)、完成下面的证明.证明:∵P、C、D都在⊙M 上,
∠P为弧CD所对的圆周角,∠CMD为弧CD所对的圆心角,
∴∠P=∠CMD( )(填推理依据).
∴∠AMD=2∠P.
21. 如图,一个单向隧道的断面,隧道顶是一条抛物线的一部分,经测量,隧道顶的跨度为4米,最高处到地面的距离为4米,两侧墙高均为3米,距左侧墙壁1米和3米时,隧道高度均为3.75米.设距左侧墙壁水平距离为x米的地点,隧道高度为y米.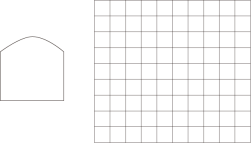
请解决以下问题:
(1)、在网格中建立适当的平面直角坐标系,根据题中数据描点,并用平滑的曲线连接;(2)、请结合所画图象,写出抛物线的对称轴;(3)、今有宽为2.4米的卡车在隧道中间行驶,如果卡车载物后的高度为3.2米,要求卡车从隧道中间通过时,为保证安全,要求卡车载物后最高点到隧道顶面对应的点的距离均不小于0.6米,结合所画图象,试判断该卡车能否通过隧道.22. 如图,在平行四边形ABCD中,过点B作BE⊥CD交CD的延长线于点E,过点C作CFEB交AB的延长线于点F. (1)、求证:四边形BFCE是矩形;(2)、连接AC,若AB=BE=2, , 求AC的长23. 如图1,一次函数y=kx+4k(k≠0)的图象与x轴交于点A,与y轴交于点B,且经过点C(2,m).
(1)、求证:四边形BFCE是矩形;(2)、连接AC,若AB=BE=2, , 求AC的长23. 如图1,一次函数y=kx+4k(k≠0)的图象与x轴交于点A,与y轴交于点B,且经过点C(2,m).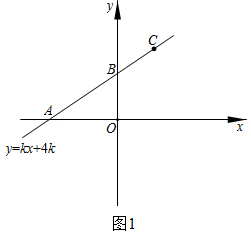
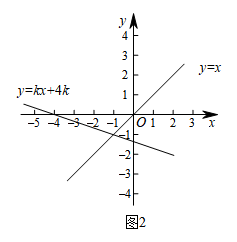 (1)、当时,求一次函数的解析式并求出点A的坐标;(2)、当x>-1时,对于x的每一个值,函数y=x的值大于一次函数y=kx+4k(k≠0)的值,求k的取值范围.24. 如图,BE是⊙O直径,点A是⊙O外一点:OA⊥OB,AP切⊙O于点P,连接BP交AO于点C.
(1)、当时,求一次函数的解析式并求出点A的坐标;(2)、当x>-1时,对于x的每一个值,函数y=x的值大于一次函数y=kx+4k(k≠0)的值,求k的取值范围.24. 如图,BE是⊙O直径,点A是⊙O外一点:OA⊥OB,AP切⊙O于点P,连接BP交AO于点C.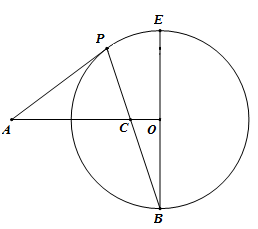 (1)、求证:∠PAO=2∠PBO;(2)、若⊙O的半径为5, , 求BP的长.25. 为庆祝中国共产党建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,继承革命先烈的优良传统,某中学开展了建党100周年知识测试.该校七、八年级各有300名学生参加,从中各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息:
(1)、求证:∠PAO=2∠PBO;(2)、若⊙O的半径为5, , 求BP的长.25. 为庆祝中国共产党建党100周年,讴歌中华民族实现伟大复兴的奋斗历程,继承革命先烈的优良传统,某中学开展了建党100周年知识测试.该校七、八年级各有300名学生参加,从中各随机抽取了50名学生的成绩(百分制),并对数据(成绩)进行整理,描述和分析,下面给出了部分信息:a.八年级的频数分布直方图如下(数据分为5组:50≤x<60﹐60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
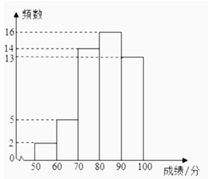
b.八年级学生成绩在80≤x<90的这一组是:
80 81 82 83 83 83.5 83.5 84 84 85 86 86.5 87 88 89 89
c.七、八年级学生成绩的平均数、中位数、众数如下:
年级
平均数
中位数
众数
七年级
87.2
85
91
八年级
85.3
m
90
根据以上信息,回答下列问题:
(1)、表中m的值为;(2)、在随机抽样的学生中,建党知识成绩为84分的学生,在年级抽样学生中排名更靠前,理由是;(3)、若成绩85分及以上为“优秀”,请估计八年级达到“优秀”的人数.26. 已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(1,0)与点C(0,-3),其顶点为P.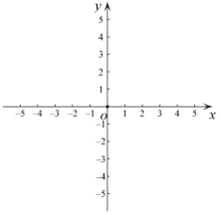 (1)、求二次函数的解析式及P点坐标;(2)、当m≤x≤m+1时,y的取值范围是-4≤y≤2m,求m的值.27. 已知:等边△ABC,过点B作AC的平行线l.点P为射线AB上一个动点(不与点A,B重合),将射线PC绕点P顺时针旋转60°交直线l于点D.
(1)、求二次函数的解析式及P点坐标;(2)、当m≤x≤m+1时,y的取值范围是-4≤y≤2m,求m的值.27. 已知:等边△ABC,过点B作AC的平行线l.点P为射线AB上一个动点(不与点A,B重合),将射线PC绕点P顺时针旋转60°交直线l于点D.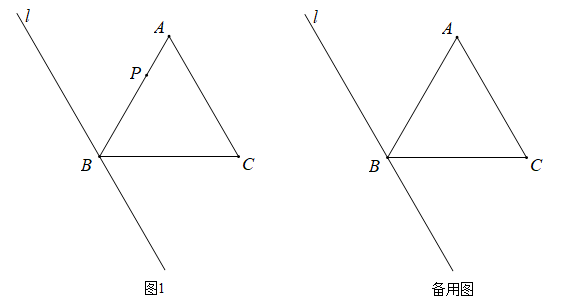 (1)、如图1,点P在线段AB上时,依题意补全图形;
(1)、如图1,点P在线段AB上时,依题意补全图形;①求证:∠BDP=∠PCB;
②用等式表示线段BC,BD,BP之间的数里关系,并证明;
(2)、点P在线段AB的延长线上,直接写出线段BC,BD,BP之间的数量关系.28. 如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P,Q两点(Q在P,H之间).我们把点P称为⊙I关于直线a的“远点”,把PQ·PH的值称为⊙I关于直线a的“特征数”.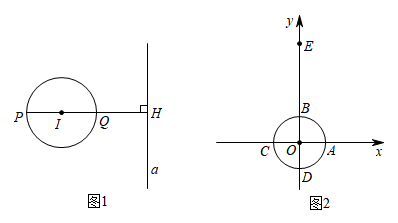 (1)、如图2,在平面直角坐标系xOy中,点E的坐标为(0,4),半径为1的⊙O与两坐标轴交于点A,B,C,D.
(1)、如图2,在平面直角坐标系xOy中,点E的坐标为(0,4),半径为1的⊙O与两坐标轴交于点A,B,C,D.①过点E作垂直于y轴的直线m﹐则⊙O关于直线m的“远点”是点 ▲ (填“A”,“B”,“C”或“D”),⊙O关于直线m的“特征数”为 ▲ ;
②若直线n的函数表达式为 , 求⊙O关于直线n的“特征数”;
(2)、在平面直角坐标系xOy、中,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线l相离,点N(–1,0)是⊙F关于直线l的“远点”,且⊙F关于直线l的“特征数”是 , 直接写出直线l的函数解析式.