北京市朝阳区2022年中考一模数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 如图是某几何体的三视图,该几何体是( )
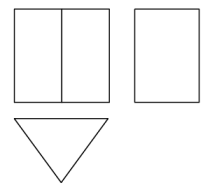 A、三棱柱 B、长方体 C、圆锥 D、圆柱2. 2022年3月5日,国务院总理李克强代表国务院,向十三届全国人大五次会议作政府工作报告.报告中指出过去一年是党和国家历史上具有里程碑意义的一年,“十四五”实现良好开局,我国发展又取得新的重大成就.2021年国内生产总值达114万亿元,增长 . 将1140000用科学记数法表示应为( )A、 B、 C、 D、3. 实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( )
A、三棱柱 B、长方体 C、圆锥 D、圆柱2. 2022年3月5日,国务院总理李克强代表国务院,向十三届全国人大五次会议作政府工作报告.报告中指出过去一年是党和国家历史上具有里程碑意义的一年,“十四五”实现良好开局,我国发展又取得新的重大成就.2021年国内生产总值达114万亿元,增长 . 将1140000用科学记数法表示应为( )A、 B、 C、 D、3. 实数a,b在数轴上对应的点的位置如图所示,下列结论中正确的是( ) A、 B、 C、 D、4. 将一副三角尺(厚度不计)如图摆放,使有刻度的两条边互相平行,则图中的大小为( )
A、 B、 C、 D、4. 将一副三角尺(厚度不计)如图摆放,使有刻度的两条边互相平行,则图中的大小为( ) A、 B、 C、 D、5. 下列多边形中,内角和与外角和相等的是( )A、
A、 B、 C、 D、5. 下列多边形中,内角和与外角和相等的是( )A、 B、
B、 C、
C、 D、
D、 6. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 下图是国家统计局公布的2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数分别为 , 方差分别为 , 则( )
6. 不透明袋子中装有红、绿小球各一个,除颜色外无其他差别,随机摸出一个小球后,放回并摇匀,再随机摸出一个,两次都摸到红球的概率为( )A、 B、 C、 D、7. 下图是国家统计局公布的2021年居民消费价格月度涨跌幅度,月度同比和月度环比的平均数分别为 , 方差分别为 , 则( ) A、 B、 C、 D、8. 点在反比例函数的图象上,下列推断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、存在 , 使得
A、 B、 C、 D、8. 点在反比例函数的图象上,下列推断正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、存在 , 使得二、填空题
-
9. 若代数式 有意义,则实数x的取值范围是.10. 分解因式 .11. 写出一个比4大且比5小的无理数 .12. 如图,是的弦,是的切线,若 , 则 .
 13. 如图,在中, , 点D在上(不与点A,C重合),只需添加一个条件即可证明和相似,这个条件可以是(写出一个即可).
13. 如图,在中, , 点D在上(不与点A,C重合),只需添加一个条件即可证明和相似,这个条件可以是(写出一个即可). 14. 如图,2022年北京冬奥会上,一些可看作正六边形的“小雪花”对称地排列在主火炬周围,中间空出了13个“小雪花”的位置来突出主火炬,在其中91个“小雪花”上面写有此次参会的国家或地区的名称,此外还有几个“小雪花”上面只有中国结图案,这些只有中国结图案的“小雪花”共有个.
14. 如图,2022年北京冬奥会上,一些可看作正六边形的“小雪花”对称地排列在主火炬周围,中间空出了13个“小雪花”的位置来突出主火炬,在其中91个“小雪花”上面写有此次参会的国家或地区的名称,此外还有几个“小雪花”上面只有中国结图案,这些只有中国结图案的“小雪花”共有个. 15. 若关于x的一元二次方程有一个根是 , 则 .16. 尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:
15. 若关于x的一元二次方程有一个根是 , 则 .16. 尊老敬老是中华民族的传统美德,某校文艺社团的同学准备在“五一”假期去一所敬老院进行慰问演出,他们一共准备了6个节目,全体演员中有8人需参加两个或两个以上的节目演出,情况如下表:演员1
演员2
演员3
演员4
演员5
演员6
演员7
演员8
节目A
√
√
√
√
√
节目B
√
√
√
节目C
√
√
√
节目D
√
√
节目E
√
√
节目F
√
√
从演员换装的角度考虑,每位演员不能连续参加两个节目的演出,从节目安排的角度考虑,首尾两个节目分别是A,F,中间节目的顺序可以调换,请写出一种符合条件的节目先后顺序(只需按演出顺序填写中间4个节目的字母即可).
三、解答题
-
17. 计算: .18. 解不等式组:19. 已知 , 求代数式的值.20. 已知关于x的一元二次方程 .(1)、求证:该方程总有两个实数根;(2)、若该方程的两个实数根都是整数,且其中一个根是另一个根的2倍,求a的值.21. 中国古代数学家李子金在《几何易简集》中记载了圆内接正三角形的一种作法:“以半径为度,任用圆界一点为心,作两圆相交,又移一心,以交线为界,再作一交圆,其三线相交处为一角,其两线相交处为两角,直线界之亦得所求”.
由记载可得作法如下:
①作 , 在上取一点N,以点N为圆心,为半径作 , 两圆相交于A,B两点,连接;
②以点B为圆心,为半径作 , 与相交于点C,与相交于点D;
③连接 , , , .
, 都是圆内接正三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹); (2)、完成下面的证明,
(2)、完成下面的证明,证明:连接 , , , .
∵ ,
∴为① .
∴ .
同理可得, .
∴ .
∴(② )(填推理的依据).
∵ ,
∴是等边三角形.
同理可得,是等边三角形.
22. 如图,在矩形中, , 相交于点O, , .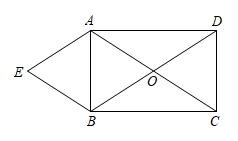 (1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.23. 如图,为的直径,C为上一点,和过点C的切线互相垂直,垂足为D.
(1)、求证:四边形是菱形;(2)、若 , 求四边形的面积.23. 如图,为的直径,C为上一点,和过点C的切线互相垂直,垂足为D. (1)、求证:平分;(2)、若 , , 求的长.24. 某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h米.
(1)、求证:平分;(2)、若 , , 求的长.24. 某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h米.d(米)
0.50
1.00
1.5
2.00
2.50
3.00
h(米)
3.75
4.00
3.75
3.00
1.75
0
请解决以下问题:
(1)、在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接; (2)、结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;(3)、求h关于d的函数表达式;(4)、公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米,工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.25. 某校初三年级有两个校区,其中甲校区有200名学生,乙校区有300名学生,两个校区所有学生都参加了一次环保知识竞赛,为了解两个校区学生的答题情况,进行了抽样调查,从甲、乙两个校区各随机抽取20名学生,对他们本次环保知识竞赛的成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.
(2)、结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;(3)、求h关于d的函数表达式;(4)、公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米,工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.25. 某校初三年级有两个校区,其中甲校区有200名学生,乙校区有300名学生,两个校区所有学生都参加了一次环保知识竞赛,为了解两个校区学生的答题情况,进行了抽样调查,从甲、乙两个校区各随机抽取20名学生,对他们本次环保知识竞赛的成绩(百分制)进行了整理、描述和分析.下面给出了部分信息.a.甲校区成绩的频数分布直方图如下(数据分成4组: , , , );

b.甲校区成绩在这一组的是:
74 74 75 77 77 77 77 78 79 79
c.甲、乙两校区成绩的平均数、中位数如下:
平均数
中位数
甲校区
79.5
m
乙校区
77
81.5
根据以上信息,回答下列问题:
(1)、写出表中m的值;(2)、两个校区分别对本次抽取的学生的成绩进行等级赋分,超过本校区的平均分就可以赋予等级A,判断在本次抽取的学生中哪个校区赋予等级A的学生更多,并说明理由;(3)、估计该校初三年级所有学生本次环保知识竞赛的平均分为(直接写出结果).26. 在平面直角坐标系中,点在抛物线上.(1)、若 , 求的值;(2)、若 , 求值的取值范围.27. 在中,D是的中点,且 , 将线段沿所在直线翻折,得到线段 , 作交直线于点E. (1)、如图,若 ,
(1)、如图,若 ,①依题意补全图形;
②用等式表示线段之间的数量关系,并证明;
(2)、若 , 上述结论是否仍然成立?若成立,简述理由:若不成立,直接用等式表示线段之间新的数量关系(不需证明).28. 在平面直角坐标系中,对于直线 , 给出如下定义:若直线与某个圆相交,则两个交点之间的距离称为直线关于该圆的“圆截距”. (1)、如图1,的半径为1,当时,直接写出直线关于的“圆截距”;(2)、点M的坐标为 ,
(1)、如图1,的半径为1,当时,直接写出直线关于的“圆截距”;(2)、点M的坐标为 ,①如图2,若的半径为1,当时,直线关于的“圆截距”小于 , 求k的取值范围;
②如图3,若的半径为2,当k的取值在实数范围内变化时,直线关于的“圆截距”的最小值为2,直接写出b的值.