安徽省滁州市定远县永康片2022年九年级第二次教学质量检测数学试题
试卷更新日期:2022-05-11 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列各题中计算错误的是( )A、 B、 C、 D、3. 据中央广播电视总台中国之声《全国新闻联播》报道,最新数据显示,2020年我国农产品加工业营业收入超过23.2万亿元,较上年增长5.2%将23.2万用科学记数法表示为( )A、 B、 C、 D、4. 若几何体的三视图如图所示,则该几何体是( )
 A、长方体 B、圆柱 C、圆锥 D、三棱柱5. 反比例函数y=的一个分支与一次函数y=x+5图象如图所示,若点A(a,1),点B(﹣2,b)都在函数y=x+5上,则k的值可能为( )
A、长方体 B、圆柱 C、圆锥 D、三棱柱5. 反比例函数y=的一个分支与一次函数y=x+5图象如图所示,若点A(a,1),点B(﹣2,b)都在函数y=x+5上,则k的值可能为( )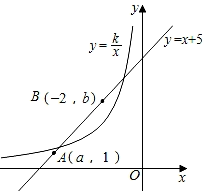 A、5 B、﹣5 C、6 D、﹣66. 2018年6月14日至7月15日世界杯在俄罗斯举行,本届赛事共有来自五大洲足联的32支球队参赛,共64场比赛,各场比赛的进球数如下表所示,对于“进球数”,以下说法正确的是( )
A、5 B、﹣5 C、6 D、﹣66. 2018年6月14日至7月15日世界杯在俄罗斯举行,本届赛事共有来自五大洲足联的32支球队参赛,共64场比赛,各场比赛的进球数如下表所示,对于“进球数”,以下说法正确的是( )进球数
0
1
2
3
4
5
6
7
场数
1
15
19
18
4
2
2
3
A、中位数是3,众数是3 B、中位数是3,众数是2 C、中位数是2,众数是3 D、中位数是2,众数是27. 如图,⊙O是△ABC的外接圆,已知∠ACO=30°,则∠B的度数为( ) A、45° B、60° C、75° D、90°8. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )
A、45° B、60° C、75° D、90°8. 如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的是( )①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
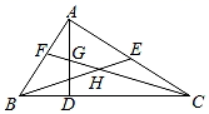 A、①②③④ B、①②③ C、②④ D、①③9. 如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当Q到达终点时,P停止移动,设PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )
A、①②③④ B、①②③ C、②④ D、①③9. 如图,边长为2的正方形ABCD,点P从点A出发以每秒1个单位长度的速度沿A-D-C的路径向点C运动,同时点Q从点B出发以每秒2个单位长度的速度沿B-C-D-A的路径向点A运动,当Q到达终点时,P停止移动,设PQC的面积为S,运动时间为t秒,则能大致反映S与t的函数关系的图象是( )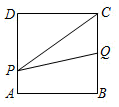 A、
A、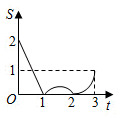 B、
B、 C、
C、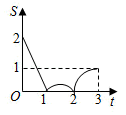 D、
D、 10. 已知抛物线在坐标系中的位置如图所示,它与 , 轴的交点分别为 , , 是其对称轴上的动点,根据图中提供的信息,以下结论中错误的是( )
10. 已知抛物线在坐标系中的位置如图所示,它与 , 轴的交点分别为 , , 是其对称轴上的动点,根据图中提供的信息,以下结论中错误的是( )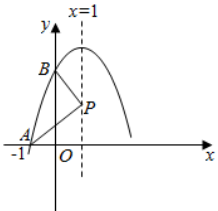 A、 B、 C、周长的最小值是 D、是的一个根
A、 B、 C、周长的最小值是 D、是的一个根二、填空题
-
11. 因式分解:.12. 要使代数式 有意义,则 的取值范围为.13. 如图,的面积为 , 的平分线与垂直,垂足为点 , , 那么的面积为 .
 14. 平面直角坐标系中,矩形OMPN的顶点P在第一象限,M在轴上,N在y轴上,点A是PN的中点,且 , 过点A的双曲线 , 与PM交于点B,过B作交轴于C,若 , 则 .
14. 平面直角坐标系中,矩形OMPN的顶点P在第一象限,M在轴上,N在y轴上,点A是PN的中点,且 , 过点A的双曲线 , 与PM交于点B,过B作交轴于C,若 , 则 .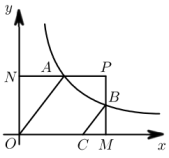
三、解答题
-
15. 计算:(1)、(2)、先化简,再求值 , 其中 , .16. 如图,在平面直角坐标系中,的三个顶点分别为 .

⑴把向右平移5个单位后得到BC , 请画出BC , 并写出的坐标;
⑵把绕点C逆时针旋转90°,得到BC , 请画出BC , 并写出的坐标.
17. 如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长(≈1.73).
 18. 如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC.
18. 如图,已知△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,BF、ED的延长线交于点G,连接GC. (1)、求证:AB=GD;(2)、当CG=EG时,且AB=2,求CE.19. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)、求证:AB=GD;(2)、当CG=EG时,且AB=2,求CE.19. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC. (1)、求证:BD是⊙O的切线;(2)、若⊙O的半径为5,sinA= , 求BH的长.20. 随着黑龙江省牡丹江市绥芬河市境外输入疫情防控形势的日益严峻,社会各界纷纷伸出援助之手.我省某企业准备购买红外线测温仪和防护服捐赠给绥芬河市,在市场上了解到某种红外线测温仪的单价比防护服多200元,且用70000元买这种测温仪的数量与用30000元买这种防护服的数量相同.(1)、求这种红外线测温仪和防护服的单价.(2)、该企业准备出资超过29.8万元又不超过30万元购买这两种防疫物资捐赠绥芬河,同时要求防护服的数量比红外线测温仪的数量多300,该企业有多少种购买方案.21. 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
(1)、求证:BD是⊙O的切线;(2)、若⊙O的半径为5,sinA= , 求BH的长.20. 随着黑龙江省牡丹江市绥芬河市境外输入疫情防控形势的日益严峻,社会各界纷纷伸出援助之手.我省某企业准备购买红外线测温仪和防护服捐赠给绥芬河市,在市场上了解到某种红外线测温仪的单价比防护服多200元,且用70000元买这种测温仪的数量与用30000元买这种防护服的数量相同.(1)、求这种红外线测温仪和防护服的单价.(2)、该企业准备出资超过29.8万元又不超过30万元购买这两种防疫物资捐赠绥芬河,同时要求防护服的数量比红外线测温仪的数量多300,该企业有多少种购买方案.21. 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:分组
频数
频率
第一组(0≤x<15)
3
0.15
第二组(15<x <30 )
6
a
第三组(30<x<45)
7
0.35
第四组(45≤x <60)
b
0.20
 (1)、频数分布表中a = ▲ , b= ▲ , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?22. 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(-1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)、频数分布表中a = ▲ , b= ▲ , 并将统计图补充完整;(2)、如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?(3)、已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?22. 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(-1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)、
求这个二次函数的表达式;
(2)、点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.23. 如图,已知:Rt△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,点P是BC边上的一个动点.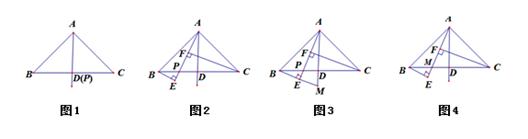 (1)、如图1,若点P与点D重合,连接AP,则AP与BC的位置关系是;(2)、如图2,若点P在线段BD上,过点B作BE⊥AP于点E,过点C作CF⊥AP于点F,则CF,BE和EF这三条线段之间的数量关系是;(3)、如图3,在(2)的条件下,若BE的延长线交直线AD于点M,求证:CP=AM;(4)、如图4,已知BC=4,若点P从点B出发沿着BC向点C运动,过点B作BE⊥AP于点E,过点C作CF⊥AP于点F,设线段BE的长度为 ,线段CF的长度为 ,试求出点P在运动的过程中 的最大值.
(1)、如图1,若点P与点D重合,连接AP,则AP与BC的位置关系是;(2)、如图2,若点P在线段BD上,过点B作BE⊥AP于点E,过点C作CF⊥AP于点F,则CF,BE和EF这三条线段之间的数量关系是;(3)、如图3,在(2)的条件下,若BE的延长线交直线AD于点M,求证:CP=AM;(4)、如图4,已知BC=4,若点P从点B出发沿着BC向点C运动,过点B作BE⊥AP于点E,过点C作CF⊥AP于点F,设线段BE的长度为 ,线段CF的长度为 ,试求出点P在运动的过程中 的最大值.