山东省泰安市宁阳县(五四制)2021-2022学年七年级下学期期中考试数学试题
试卷更新日期:2022-05-11 类型:期中考试
一、单选题
-
1. 下列是二元一次方程的是( )A、 B、 C、 D、2. 已知 是方程 的一个解,那么 的值是( )A、-2 B、2 C、-4 D、43. 已知方程 , 用含的代数式表示正确的是( )A、 B、 C、 D、4. 用加减消元法解二元一次方程组 时,下列方法中无法消元的是( )A、①×2﹣② B、②×(﹣3)﹣① C、①×(﹣2)+② D、①﹣②×35. 二元一次方程的正整数解有几个( )A、4个 B、3个 C、2个 D、1个6. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=﹣2 B、a=﹣2,b=3 C、a=2,b=﹣3 D、a=﹣3,b=27. 以下事件中:①两个奇数的乘积是奇数;②抛掷一枚均匀的骰子,朝上点数为2;③每天太阳从东边升起;④明天要下雨:⑤长分别为2,3,4的三条线段能围成一个三角形.是必然事件的有( )A、5个 B、4个 C、3个 D、2个8. 如图, ,一块含45°角的直角三角板如图放置, ,则 的度数为( )
 A、17° B、27° C、38° D、43°9. 图中以两直线 , 的交点坐标为解的方程组是( )
A、17° B、27° C、38° D、43°9. 图中以两直线 , 的交点坐标为解的方程组是( )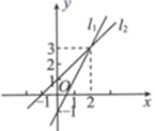 A、 B、 C、 D、10. 《九章算术》中有这样一个问题:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”题意为:今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其 的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则列方程组为( )A、 B、 C、 D、11. 如图,10块相同的小长方形墙砖拼成一个长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程正确的是( )
A、 B、 C、 D、10. 《九章算术》中有这样一个问题:“今有甲乙二人持钱不知其数,甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?”题意为:今有甲乙二人,不知其钱包里有多少钱,若乙把其一半的钱给甲,则甲的钱数为50;而甲把其 的钱给乙,则乙的钱数也能为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则列方程组为( )A、 B、 C、 D、11. 如图,10块相同的小长方形墙砖拼成一个长方形,设小长方形墙砖的长和宽分别为x厘米和y厘米,则依题意列方程正确的是( )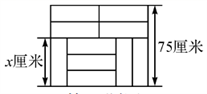 A、 B、 C、 D、12. 如图, 的角平分线 、 相交于 , , ,且 于 ,下列结论:① ;② ;③ 平分 ;④ .其中正确的结论的个数是( ).
A、 B、 C、 D、12. 如图, 的角平分线 、 相交于 , , ,且 于 ,下列结论:① ;② ;③ 平分 ;④ .其中正确的结论的个数是( ).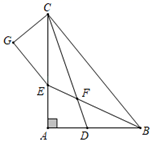 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 将命题“同角的补角相等”改写成“如果……那么……”的形式为
14. 若 ,则 的值为 .15. 如图,一次函数 与 的图象相交于点 ,则方程组 的解是 . 16. 若关于 的二元一次方程组 的解也是二元一次方程 的解;则k的值是17. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是.
16. 若关于 的二元一次方程组 的解也是二元一次方程 的解;则k的值是17. 如图,在两个同心圆中,四条直径把大圆分成八等份,若往圆面投掷飞镖,则飞镖落在黑色区域的概率是. 18. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的 处,折痕为CD , 则 = .
18. 如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上的 处,折痕为CD , 则 = .
三、解答题
-
19. 解下列方程(组):(1)、(2)、20. 对于任意有理数 , , , , 我们规定: , 根据这一规定,解答下列问题:若 , 同时满足 , , 求 , 的值.21. 今年“五一”假期期间,某超市开展有奖促销活动,凡在超市购物的顾客均有转动圆盘的机会(如图),如果规定当圆盘停下来时指针指向8就中一等奖,指向2或6就中二等奖,指向1或3或5就中纪念奖;指向其余数字不中奖.
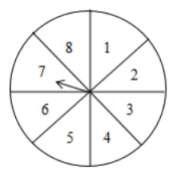 (1)、转动转盘中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、“五一”这天有1800人参与这项活动,估计获得一等奖的人数是多少?22. 已知:如图,BC∥AD,∠A=∠B.
(1)、转动转盘中一等奖、二等奖、三等奖的概率是分别是多少?(2)、顾客中奖的概率是多少?(3)、“五一”这天有1800人参与这项活动,估计获得一等奖的人数是多少?22. 已知:如图,BC∥AD,∠A=∠B. (1)、试说明BE∥AF;(2)、若∠DOB=135°,求∠A的度数.23. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)、试说明BE∥AF;(2)、若∠DOB=135°,求∠A的度数.23. 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2. (1)、试说明:DG∥BC;(2)、若 , ,求 的度数.24. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:
(1)、试说明:DG∥BC;(2)、若 , ,求 的度数.24. 春节即将来临,抗击新冠疫情防控工作至关重要,某公司加紧生产酒精消毒液与额温枪两种抗疫物质,其两种物资的生产成本和销售单价如表所示:种类
生产成本(元/件)
销售单价(元/件)
酒精消毒液
56
62
额温枪
84
100
(1)、若该公司2020年12月生产两种物资共100万件,生产总成本为7280万元,请用列二元一次方程组的方法,求该月酒精消毒液和额温枪两种物资各生产了多少万件?(2)、该公司2021年1月生产两种物资共150万件,根据市场需求,该月将举办迎新年促销活动,其中酒精消毒液的销售单价降低2元,额温枪打9折销售.若设该月生产酒精消毒液x万件,该月销售完这两种物资的总利润为y万元,求y与x之间的函数关系式.25.(1)、探究:如图1,求证:; (2)、应用:如图2, , , 求的度数.
(2)、应用:如图2, , , 求的度数.