山东省济宁市邹城市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2022-05-11 类型：期中考试

进入出卷网下载

一、单选题

1. 已知点P的坐标是（5，－2），则点P在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 如图，直线EF和直线AB交于点E，和直线CD交于点F，不能判定 $A B ∥ C D$ 的条件是（）

A、 $∠ 1 = ∠ 2$ B、 $∠ 1 = ∠ 4$ C、 $∠ 2 = ∠ 4$ D、 $∠ 1 + ∠ 3 = 180 °$

查看试题解析
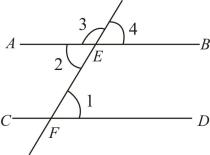3. 下列说法错误的是（）

A、－4是16的平方根 B、－8立方根是－2 C、－1的平方根是 $± 1$ D、16的算术平方根是4

查看试题解析
4. 在实数： $3.14159$ ， $\sqrt[3]{64}$ ， $\sqrt{5}$ ， $\sqrt{9}$ ， $4 . \dot{2} \dot{1}$ ， $π$ ， $\frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 如图所示，在数轴上表示实数 $\sqrt{14}$ 的点可能是（）

A、点M B、点N C、点P D、点Q

查看试题解析
6. 如图，已知 $A B ∥ C D ， A E$ 平分 $∠ C A B$ ，且交 $C D$ 于点 $D$ ， $∠ C = 110 °$ ，则 $∠ A D C$ 为（）

A、30° B、35° C、40° D、45°

查看试题解析
7. 若|2﹣m|+ $\sqrt{10 + n}$ ＝0，则m+n的立方根是（）

A、2 B、﹣2 C、﹣4 D、﹣8

查看试题解析
8. 已知线段CD是由线段AB平移得到的，点A（–1，4）的对应点为C（4，7），则点B（–4，–1）的对应点D的坐标为（）

A、（1，2） B、（2，9） C、（5，3） D、（–9，–4）

查看试题解析
9. 如图，有A，B，C三个地点，且AB⊥BC，从A地测得B地在A地的北偏东43°的方向上，那么从B地测得C地在B地的（）

A、南偏西43° B、南偏东43° C、北偏东47° D、北偏西47°

查看试题解析
10. 如图，在平面直角坐标系中，A（1，1），B（－1，1），C（－1，－2），D（1，－2）．把一条长为2022个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A处，并按A－B－C－D－A－…的规律紧绕在四边形ABCD的边上，则细线另一端所在位置的点的坐标是（）

A、（－1，1） B、（－1，－1） C、（－1，－2） D、（0，－2）

查看试题解析

二、填空题

11. $\sqrt{4}$ 的值是．

查看试题解析
12. 点A的坐标是（－3，1），那么点A到x轴的距离是．

查看试题解析
13. 把命题“同角的余角相等”改写成“如果…那么…”的形式．

查看试题解析
14. 如图， $∠ 1 = ∠ 2$ ， $∠ 3 = 123 °$ ，则 $∠ 4$ 等于．

查看试题解析
15. 已知点M的坐标为 $(a - 2 ， 2 a - 3)$ ，点N的坐标为（1，5），直线 $M N ∥ x$ 轴，则点M的横坐标为．

查看试题解析
16. 若一个正数的平方根是 $3 x - 5$ 与 $7 - x$ ，则这个正数是．

查看试题解析
17. 若 $\sqrt{20 n}$ 是整数，则正整数n的最小值为．

查看试题解析
18. 如图，长方形纸片的对边是平行的，小明将含有30°角的三角板的直角顶点放在一边上，含有60°角的顶点放在邻边上，若 $∠ 1 = 42 ° 3 2^{'}$ ，则 $∠ 2$ 的度数为．

查看试题解析

三、解答题

19. 一动物园景区图如图所示，请你在图中建立平面直角坐标系，使马的坐标为（－3，－3），并用坐标表示出其他景点所在的位置．
狮子：；南门：飞禽：；两栖动物：

查看试题解析
20. 已知：如图， $∠ B A P + ∠ A P D = 180 °$ ， $∠ 1 = ∠ 2$ ．求证： $∠ E = ∠ F$ ．
证明：∵ $∠ B A P + ∠ A P D = 180 °$ ，（    ）
∴ $A B ∥ C D$ ．（   ）
∴ $∠ B A P = ∠ A P C$ ．（   ）
∵ $∠ 1 = ∠ 2$ ，（   ）
∴ $∠ B A P - ∠ 1 = ∠ A P C - ∠ 2$ ．（   ）
即 $∠ E A P = ∠ F P A$ ．
∴                  ▲                   ．（   ）
∴ $∠ E = ∠ F$ ．（   ）

查看试题解析
21.

(1)、计算： $\sqrt{3} (\sqrt{2} + | \sqrt{2} - \sqrt{3} |)$ ；

(2)、已知 ${(x - 1)}^{2} = 4$ ，求x的值．

查看试题解析
22. 如图，直角坐标系中，三角形ABC的顶点坐标分别为A（1，－2），B（3，4），C（－1，2）．

(1)、将三角形ABC先向左平移1个单位长度，再向上平移2个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ，画出三角形 $A^{'} B^{'} C^{'}$ ，并写出三个顶点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(2)、若点P（a，b）是三角形ABC的边AB上一点，经过（1）中的平移后点P到达 $P^{'}$ 点的位置，则 $P^{'}$ 点的坐标为；

(3)、求三角形ABC的面积．

查看试题解析
23. 如图，直线AB，CD相交于点O，OE平分 $∠ B O D$ ， OF平分 $∠ B O C$ ， $∠ A O D ： ∠ B O D = 2 ： 1$ ．

(1)、求 $∠ D O E$ 的度数；

(2)、求 $∠ E O F$ 的度数．

(3)、如果 $B E ∥ O F$ ， $∠ E = ∠ F$ ，请问：OE，BF平行吗？为什么？

查看试题解析
24. 先阅读下面的文字，再解答问题：
大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $(\sqrt{2} - 1)$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理的，因为 $\sqrt{2}$ 的整数部分是1，将这个数减去其整数部分，差就是小数部分．
又例如：∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ， ∴ $\sqrt{7}$ 的整数部分为2，小数部分为 $(\sqrt{7} - 2)$ ．
请解答：

(1)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求 $a + b - \sqrt{5}$ 的值；

(2)、已知： $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x - y$ 的值．

查看试题解析