广东省韶关市2021-2022学年七年级下学期期中数学试题

试卷更新日期：2022-05-11 类型：期中考试

进入出卷网下载

一、单选题

1. $- 8$ 的立方根是（）

A、4 B、±2 C、2 D、 $- 2$

查看试题解析
2. 下列实数，是无理数的是（）

A、﹣5 B、 $\sqrt{3}$ C、﹣0.1 D、 $\frac{22}{7}$

查看试题解析
3. 点 $(- 2 ， 6)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列A、B、C、D四幅图案中，能通过平移图案得到的是（）

A、 B、 C、 D、

查看试题解析
5. 下列计算错误的是（）

A、± $\sqrt{9} =$ ±3 B、 $\sqrt{16} =$ 4 C、（ $\sqrt{3}$ ）²＝3 D、 $\sqrt{(- 3)^{2}} = -$ 3

查看试题解析
6. 如果点P(m＋3，m＋1)在直角坐标系的x轴上,那么P点坐标为（）

A、(0,2) B、(2,0) C、(4,0) D、(0,-4)

查看试题解析
7. 将点A $(- 2 ， - 3)$ 向左平移3个单位，再向上平移4个单位得到点B，则点B的坐标是（）

A、（-5，-7） B、（-5，1） C、（1，1） D、（1，-7）

查看试题解析
8. 如图，现要从村庄 $A$ 修建一条连接公路 $C D$ 的最短小路，过点 $A$ 作 $A B ⊥ C D$ 于点 $B$ ，沿 $A B$ 修建公路，则这样做的理由是（）

A、垂线段最短 B、两点之间，线段最短 C、过一点可以作无数条直线 D、两点确定一条直线

查看试题解析
9. 如图，有一条直的宽纸带，按图折叠，则∠α的度数等于（　　）

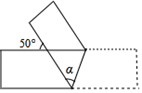A、50° B、65° C、75° D、80°

查看试题解析
10. 现规定一种运算： $a ※ b = a b + a - b$ ，其中 $a$ ， $b$ 为实数，则 $\sqrt{16} ※ \sqrt[3]{- 8}$ 等于（）

A、-2 B、-6 C、2 D、6

查看试题解析

二、填空题

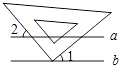
11. “对顶角相等”是命题．（填“真”或“假”）

查看试题解析
12. 在平面直角坐标系中，点P的坐标是（3，﹣4），则点P到x轴的距离为．

查看试题解析
13. ﹣64的立方根是； $16$ 的算术平方根是．

查看试题解析
14. 如图，已知a∥b，小亮把三角板的直角顶点放在直线b上．若∠1=40°，则∠2的度数为．

查看试题解析
15. 若（a﹣3）² $+ \sqrt{b + 1} =$ 0．则a+b＝．

查看试题解析
16. 如图，直线AB、CD相交于点O，OE⊥AB于点O，且∠COE＝34°，则∠AOD为．

查看试题解析
17. 在平面直角坐标系中，以任意两点 P（x₁ ， y₁），Q（x₂ ， y₂）为端点的线段的中点坐标为 $(\frac{x_{1} + x_{2}}{2} ， \frac{y_{1} + y_{2}}{2})$ ．现有 A（3，4），B（1，8），C（2，6）三点，点D为线段AB的中点，点C 为线段AE的中点，则线段DE的中点坐标为．

查看试题解析

三、解答题

18. 计算：| $\sqrt{3} -$ 3| $- \sqrt{16} + \sqrt[3]{1}$ ．

查看试题解析
19. 求下列各式中的x．

(1)、4x²＝81；

(2)、（x+3）³＝﹣27．

查看试题解析
20. 已知：如图，AB//CD，∠B＝∠D，求证：∠E＝∠BCA．（完成下列推理证明）
证明：∵AB∥CD（已知）
∴∠B＝∠                  ▲                  （两直线平行，内错角相等）
∵∠B＝∠D（已知）
∴∠D＝∠                  ▲                  （   ）
∴ED//                  ▲                  （   ）
∴∠E＝∠BCA（  ）

查看试题解析
21. 已知一个数m的两个不相等的平方根分别为a＋2和3a－6．

(1)、求a的值；

(2)、求这个数m．

查看试题解析
22. 如图，AB⊥CD，AB⊥EF．求证：∠1＝∠3．

查看试题解析
23. 已知点 $P (2 m + 4 ， m - 1)$ ，请分别根据下列条件，求出点P的坐标．

(1)、点P在x轴上，则P点坐标为；

(2)、点P的横坐标比纵坐标大3；

(3)、点P在过点 $A (2 ， 4)$ 且与y轴平行的直线上．

查看试题解析
24. 已知在平面直角坐标系中有三点A（﹣2，1）、B（3，1）、C（2，3）．请回答如下问题：

(1)、在坐标系内描出△ABC的位置；

(2)、求出△ABC的面积；

(3)、在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10，若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
25. 如图（1），AB∥CD，猜想∠BPD与∠B．∠D的关系，说明理由．（提示：三角形的内角和等于180°）
①填空或填写理由
解：猜想∠BPD+∠B+∠D=360°
理由：过点P作EF∥AB，
∴∠B+∠BPE=180°                  ▲
∵AB∥CD，EF∥AB，
∴                  ▲                  ∥                  ▲                   ，（如果两条直线都和第三条直线平行，那么这两条直线也互相平行）
∴∠EPD+                  ▲                  =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
②依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B．∠D的关系，并说明理由．

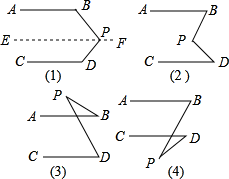
③观察图（3）和（4），已知AB∥CD，直接写出图中的∠BPD与∠B．∠D的关系，不说明理由．

查看试题解析