广东省茂名高州市十校2021-2022学年七年级下学期期中考试数学试题（A卷）

试卷更新日期：2022-05-11 类型：期中考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（）

A、 $x^{3} + x^{3} = x^{6}$ B、 $2 x \cdot 3 x^{2} = 6 x^{3}$ C、 $(2 x)^{3} = 6 x^{3}$ D、 $(2 x^{2} + x) \div x = 2 x$

查看试题解析
2. 已知：a＋b＝m，ab＝－4，化简（a－2）（b－2）的结果是（）.

A、6 B、2m－8 C、2m D、－2m

查看试题解析
3. 下列长度的三根木棒首尾相接，不能做成三角形框架的是( )

A、5cm、7cm、2cm B、7cm、13cm、10cm C、5cm、7cm、11cm D、5cm、10cm、13cm

查看试题解析
4. 如图，直线l₁∥l₂ ，则∠α＝（）

A、150° B、140° C、130° D、120°

查看试题解析
5. 下列关系式中，正确的是（）

A、 $(a + b)^{2} = a^{2} - 2 a b + b^{2}$ B、 $(a - b)^{2} = a^{2} - b^{2}$ C、 $(a + b) (- a + b) = b^{2} - a^{2}$ D、 $(a + b) (- a - b) = a^{2} - b^{2}$

查看试题解析
6. 如图，图象（折线OEFPMN）描述了某汽车在行驶过程中速度与时间的关系，下列说法中错误的是（）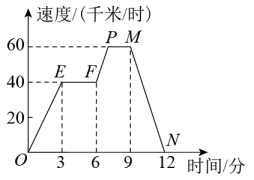

A、第3分时汽车的速度是40千米/时 B、第12分时汽车的速度是0千米/时 C、从第3分到第6分，汽车行驶了150千米 D、从第9分到第12分，汽车的速度从60千米/时减少到0千米/时

查看试题解析
7. 如图，P为 $△ A B C$ 的边 $A B$ 、 $A C$ 的垂线的交点， $∠ A = 52 °$ ，则 $∠ B P C$ 的度数为（）

A、128° B、26° C、38° D、28°

查看试题解析
8. 观察以下一列数的特点：0，1，﹣4，9，﹣16，25，…，则第11个数是（）

A、﹣121 B、﹣100 C、100 D、121

查看试题解析
9. 一辆公共汽车从车站开出，加速行驶一段后开始匀速行驶，过了一段时间，汽车到达下一个车站．乘客上、下车后汽车开始加速，一段时间后又开始匀速行驶，下面哪幅图可以近似地刻画出汽车在这段时间内的速度变化情况（）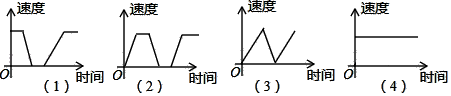

A、第（1）幅图 B、第（2）幅图 C、第（3）幅图 D、第（4）幅图

查看试题解析
10. 如图，在△ABC中，AB＝AC，BE＝CD，BD＝CF，若∠EDF＝48°，则∠A的度数为（）

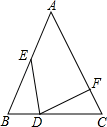A、48 B、64° C、68° D、84

查看试题解析

二、填空题

11. 已知单项式3x²y³与﹣5x²y²的积为mx⁴yⁿ ，那么m﹣n= ．

查看试题解析
12. 如图，在△ABC中，∠C＝∠ABC＝2∠A ， BD是边AC上的高，则∠DBC的大小等于度．

查看试题解析
13. 已知 $(x + a) (x + b) = x^{2} - 13 x + 36$ ，则 $a^{2} + b^{2}$ 的值是

查看试题解析
14. 二次三项式 $x^{2} - k x + 9$ 是一个完全平方式，则k=.

查看试题解析
15. 已知x+ $\frac{1}{x}$ =5，那么x²+ $\frac{1}{x^{2}}$ = ．

查看试题解析
16. 如图，∆ABC中， $∠ A = 60 ° ， ∠ B = 70 ° ，$ CD是∠ACD的平分线，点E在AC上， $D E ∥ B C$ ，则∠EDC的度数为．

查看试题解析
17. 对于任何实数，我们规定符号 $| \begin{array}{l} a c \\ b d \end{array} |$ 的意义 $| \begin{array}{l} a c \\ b d \end{array} |$ =ad-bc，按照这个规定请你计算：当 $x^{2} - 3 x + 1 = 0$ 时，求 $| \begin{array}{l} x + 1 x - 2 \\ 3 x x - 1 \end{array} |$ 的值．

查看试题解析

三、解答题

18. 计算：

(1)、 $(3 m^{2} n)^{2} \cdot (- 2 m^{2})^{3} \div (- m^{2} n)^{2}$

(2)、 $- 1^{2} + (π - 3.14)^{0} - (- \frac{1}{3})^{- 2} + (- 2)^{3}$

查看试题解析
19. 把下列每步推理的依据填在每步后面的括号里．
⑴如图①，已知DF $∥$ AB，DE $∥$ AC．
因为DF $∥$ AB，
所以∠FDE＝∠BED（  ），
因为DE $∥$ AC，
所以∠BED＝∠A（    ），
所以∠FDE＝∠A（    ）；
⑵如图②，已知∠A＝∠F，∠C＝∠D．
因为∠A＝∠F，
所以AC $∥$ DF（    ），
所以∠D＝∠1（     ），
又因为∠C＝∠D，
所以∠1＝∠C（     ），
所以BD $∥$ CE（     ）．

查看试题解析
20. 一列快车、一列慢车同时从相距300km的两地出发，相向而行，如图，分别表示两车到目的地的距离s（km）与行驶时间t（h）的关系．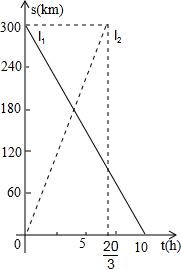

(1)、快车的速度为 km/h，慢车的速度为km/h；

(2)、经过多久两车第一次相遇？

(3)、当快车到达目的地时，慢车距离目的地多远？

查看试题解析
21. 已知∠α，∠β和线段c，求作△ABC，使∠A= ∠α，∠B=∠β，AB=c.（不写作法，保留痕迹）

查看试题解析
22. 如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．∠1=∠2，∠3=105°，求∠ACB的度数．

查看试题解析
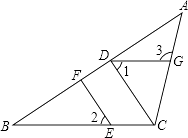23. 如图，∠BAD＝∠CAE＝90°，AB＝AD，AE＝AC，AF⊥CB，垂足为F．

(1)、求证：△ABC≌△ADE；

(2)、求∠FAE的度数；

查看试题解析
24. 我国宋朝数学家杨辉在他的著作《详解九章算法》中提出“杨辉三角”（如图），此图揭示了（a＋b）n（n为非负整数）展开式的项数及各项系数的有关规律．例如：（a＋b）⁰＝1，它只有一项，系数为1；（a＋b）¹＝a＋b，它有两项，系数分别为1，1，系数和为2；（a＋b）²＝a²＋2ab＋b² ，它有三项，系数分别为1，2，1，系数和为4；（a＋b）³＝a³＋3a²b＋3ab²＋b³ ，它有四项，系数分别为1，3，3，1，系数和为8；…
根据以上规律，解答下列问题：

(1)、（a＋b）⁴展开式共有项，系数分别为；

(2)、（a＋b）n展开式共有项，系数和为；

(3)、计算： $2^{5} + 5 \times 2^{4} + 10 \times 2^{3} + 10 \times 2^{2} + 5 \times 2 + 1 .$

查看试题解析
25. 已知动点P以2cm/s的速度沿图1所示的边框从B-C-E-F-A的路径运动，记三角形ABP的面积为S $c m^{2}$ ， S与运动时间t（s）的关系如图2所示，若AB=6cm请回答下列问题：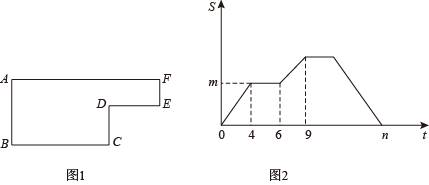

(1)、图1中BC= cm， CD= cm， DE= cm

(2)、求图2中m，n的值；

(3)、分别求出点P在线段BC和DE上运动时S与t的关系式并写出t的取值范围．

查看试题解析