江西省吉安市十校联盟2021-2022学年九年级下学期期中考试数学试题
试卷更新日期:2022-05-11 类型:期中考试
一、单选题
-
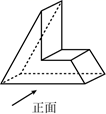
1. -5的倒数等于( )A、-5 B、5 C、 D、2. 如图,该几何体的左视图是( )
 A、
A、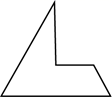 B、
B、 C、
C、 D、
D、 3. 如图,直线 ,则 ( )
3. 如图,直线 ,则 ( )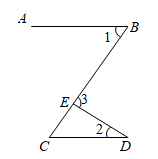 A、 B、 C、 D、4. 某校有4000名学生,随机抽取了400名学生进行体重调查,下列说法错误的是( )A、总体是该校4000名学生的体重 B、个体是每一个学生 C、样本是抽取的400名学生的体重 D、样本容量是4005. 如图3,四边形ABCD是⊙O的内接四边形,∠B=90°,∠A=60°,AB=3,CD=2,则AD的长为( )
A、 B、 C、 D、4. 某校有4000名学生,随机抽取了400名学生进行体重调查,下列说法错误的是( )A、总体是该校4000名学生的体重 B、个体是每一个学生 C、样本是抽取的400名学生的体重 D、样本容量是4005. 如图3,四边形ABCD是⊙O的内接四边形,∠B=90°,∠A=60°,AB=3,CD=2,则AD的长为( ) A、 B、 C、 D、36. 二次函数y=ax2+bx+c的图象如图,给出下列列结论:①②③ ④ . 其中,正确的结论是( )
A、 B、 C、 D、36. 二次函数y=ax2+bx+c的图象如图,给出下列列结论:①②③ ④ . 其中,正确的结论是( ) A、①②③ B、①③ C、②④ D、①②④
A、①②③ B、①③ C、②④ D、①②④二、填空题
-
7. 地球上的海洋面积约为361000000km2 , 则科学记数法可表示为 km2 .8. 若 ,则 的值为 .9. 已知两个相似多边形的周长比为1:2,它们的面积和为100,则较小多边形的面积是 .10. 关于x的方程 有两个实数根 , ,且 ,那么m的值为 .11. 如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB=5,AE=DG=1,则BF=.
 12. 如图,在矩形ABCD中,AB=6,AD=10,点E在边AD上运动,将△DEC沿EC翻折,使点D落在点D'处,若△DEC有两条边存在2倍的数量关系,则点D'到AD的距离是 .
12. 如图,在矩形ABCD中,AB=6,AD=10,点E在边AD上运动,将△DEC沿EC翻折,使点D落在点D'处,若△DEC有两条边存在2倍的数量关系,则点D'到AD的距离是 .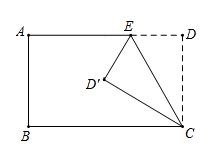
三、解答题
-
13.(1)、计算:(2)、如图,分别以△ABC的边AB、AC向外作等边△ABE和等边△ACD,直线BD与直线CE相交于点O.求证:CE=BD.
 14. 先化简,再求值.
14. 先化简,再求值.,请从不等式组 的整数解中选择一个你喜欢的求值.
15. 现有四张完全相同的不透明卡片,其正面分别写有数字-3,-1,0,3,把这四张卡片背面朝上洗匀后放在桌面上.(1)、随机抽取一张卡片,则抽取的卡片上数字为负数的概率等于;(2)、先随机抽取一张卡片,其上的数字作为点A的横坐标,然后放回并洗匀,再随机抽取一张卡片,其上的数字作为点A的纵坐标,试用画树状图或列表的方法求出点A在直线上的概率.16. 如图,已知菱形ABCD,请仅用无刻度直尺按下列要求作图(保留作图痕迹) (1)、如图1,点E,F分别是AD,AB的中点,以EF为边画一矩形;(2)、如图2,点E是对角线AC上的点, , , 以DE为边画一个正方形.17. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)、如图1,点E,F分别是AD,AB的中点,以EF为边画一矩形;(2)、如图2,点E是对角线AC上的点, , , 以DE为边画一个正方形.17. 如图,一次函数 的图象与反比例函数 的图象相交于 , 两点. (1)、求一次函数和反比例函数的表达式;(2)、直线 交x轴于点C,点P是x轴上的点,若 的面积是 ,求点P的坐标.18. 下表是2021年三月份某居民小区随机抽取20户居民的用水情况:
(1)、求一次函数和反比例函数的表达式;(2)、直线 交x轴于点C,点P是x轴上的点,若 的面积是 ,求点P的坐标.18. 下表是2021年三月份某居民小区随机抽取20户居民的用水情况:月用水量/吨
15
20
25
30
35
40
45
户数
2
4
m
4
3
0
1
月用水梯级标准
Ⅰ级(30吨以内含30吨)
Ⅱ级(超过30吨的部分)
单价(元/吨)
2.4
4
 (1)、m= ▲ , 补全图中三月份用水量的条形统计图;(2)、根据上表中的有关信息,分别写出众数 , 中位数 .(3)、为了倡导节约用水的常识,自来水公司实行“梯级用水,分类计费”,价格表如上,如果该小区有500户家庭,请估算该小区三月份有多少户家庭在Ⅰ级标准?(4)、按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?19. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A,B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?20. 小明在学校阅览室看到如图1所示的一个报刊支架, 图2为它的侧面示意图, 已知AB=BC=BD=60 cm,∠CBD=40°.
(1)、m= ▲ , 补全图中三月份用水量的条形统计图;(2)、根据上表中的有关信息,分别写出众数 , 中位数 .(3)、为了倡导节约用水的常识,自来水公司实行“梯级用水,分类计费”,价格表如上,如果该小区有500户家庭,请估算该小区三月份有多少户家庭在Ⅰ级标准?(4)、按上表收费,如果某用户本月交水费120元,请问该用户本月用水多少吨?19. 某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.(1)、A,B两款保温杯的销售单价各是多少元?(2)、由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?20. 小明在学校阅览室看到如图1所示的一个报刊支架, 图2为它的侧面示意图, 已知AB=BC=BD=60 cm,∠CBD=40°. (1)、如图2, 挂在B处报纸的垂落长度是50 cm, 为了摆放的整齐和美观, 要求报纸与地面的距离至少为10 cm,通过计算说明该报纸挂在B点处是否合理?(2)、如图3,小明站在报刊支架前的点H处观察报刊支架(点D、C、H在同一水平线上),测得CH=99 cm,小明的眼睛到地面的高度GH为160 cm,当小明的视线恰好落在点B处时,求∠G的度数.(结果精确到0.1 cm.参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364, sin40°≈ 0.643, cos40°≈0.766,tan40°≈0.839, sin49°≈0.755,cos49°≈0.656,tan49°≈1.150.)21. 如图,与等边的边 , 分别交于点D,E,是直径,过点D作于点F.
(1)、如图2, 挂在B处报纸的垂落长度是50 cm, 为了摆放的整齐和美观, 要求报纸与地面的距离至少为10 cm,通过计算说明该报纸挂在B点处是否合理?(2)、如图3,小明站在报刊支架前的点H处观察报刊支架(点D、C、H在同一水平线上),测得CH=99 cm,小明的眼睛到地面的高度GH为160 cm,当小明的视线恰好落在点B处时,求∠G的度数.(结果精确到0.1 cm.参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364, sin40°≈ 0.643, cos40°≈0.766,tan40°≈0.839, sin49°≈0.755,cos49°≈0.656,tan49°≈1.150.)21. 如图,与等边的边 , 分别交于点D,E,是直径,过点D作于点F. (1)、求证:是的切线;(2)、连接 , 当是的切线时,求半径r与等边边长a的比值.22. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C.
(1)、求证:是的切线;(2)、连接 , 当是的切线时,求半径r与等边边长a的比值.22. 如图,若抛物线y=x2+bx+c与x轴相交于A,B两点,与y轴相交于点C,直线y=x﹣3经过点B,C. (1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.
(1)、求抛物线的解析式;(2)、点P是直线BC下方抛物线上一动点,过点P作PH⊥x轴于点H,交BC于点M,连接PC.①线段PM是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点P运动的过程中,是否存在点M,恰好使△PCM是以PM为腰的等腰三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
23. 已知,如图1图2,在等腰三角形ABC中,AB=AC.平面内任意一点D,连接AD,点E是AD的中点.△ABC的角平分线AP交BC于点P,点F是射线AP上的一个动点,且AF﹥AP.若G,H是射线BC上的两个动点(点G在点H的左侧),GH=AF,点M始终是GH的中点,连接G,F,H,D,四边形GFHD是平行四边形. (1)、【感知探究一】
(1)、【感知探究一】如图1,当点D在线段AP上时,ME与GM的位置关系为 , ME与GM的数量关系为
(2)、【感知探究二】如图2,当点D不在射线AP上时,连接ME,试问ME与GM的数量关系和位置关系怎样?请说明理由;
(3)、【应用升华】如图3,在△ABP中,BC⊥AP于点M,DC⊥BC于点C,MC=AP,PM=DC,连接AD,点E是AD中点,连接ME,若ME=4,AB= . , 求DC的长.