2022年甘肃省兰州市中考数学模拟试卷四(5月份)
试卷更新日期:2022-05-10 类型:中考模拟
一、单选题(每题3分,共30分)
-
1. 科学防疫从勤洗手开始,一双没洗干净的手上带有各种细菌病毒大约850000000个,这个数据用科学记数法表示为( )A、 B、 C、 D、2. 若 , 则下列图中能直接利用“两直线平行,内错角相等”判定的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若(ax-b)(3x+4)=bx2 +cx+72,则a+b+c的值为( )A、-6 B、6 C、18 D、364. 下列计算错误的是( )A、(-5)+5=0 B、 ×|(-2)3|=- C、(-1)3+(-1)2=0 D、4÷2× ÷2=25. 中国高铁目前是世界高铁的领跑者,无论里程和速度都是世界最高的.郑州、北京两地相距约 , 乘高铁列车从郑州到北京比乘特快列车少用 , 已知高铁列车的平均行驶速度是特快列车的2.8倍,设特快列车的平均行驶速度为 , 则下面所列方程中正确的是( )A、 B、 C、 D、6. 为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m2 , 打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图像如图所示,下列说法不正确的是( )
3. 若(ax-b)(3x+4)=bx2 +cx+72,则a+b+c的值为( )A、-6 B、6 C、18 D、364. 下列计算错误的是( )A、(-5)+5=0 B、 ×|(-2)3|=- C、(-1)3+(-1)2=0 D、4÷2× ÷2=25. 中国高铁目前是世界高铁的领跑者,无论里程和速度都是世界最高的.郑州、北京两地相距约 , 乘高铁列车从郑州到北京比乘特快列车少用 , 已知高铁列车的平均行驶速度是特快列车的2.8倍,设特快列车的平均行驶速度为 , 则下面所列方程中正确的是( )A、 B、 C、 D、6. 为了让更多的学生学会游泳,少年宫新建一个游泳池,其容积为480m2 , 打开进水口注水时,游泳池的蓄水量y(m3)与注水时间t(h)之间满足一次函数关系,其图像如图所示,下列说法不正确的是( ) A、注水2小时,游泳池的蓄水量为380m3 B、该游泳池内开始注水时已经蓄水100m3 C、注水2小时,还需注水100m3 , 可将游泳池注满 D、每小时可注水190m37. 定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的一些结论,其中不正确的是( )A、当m=-3时,函数图象的顶点坐标是( , ) B、当m>0时,函数图象截x轴所得的线段长度大于 C、当m≠0时,函数图象经过同一个点 D、当m<0时,函数在x> 时,y随x的增大而减小8. 如图,在正方形 外取一点 ,连接 , , .过点 作 的垂线交 于点 .若 , .下列结论:
A、注水2小时,游泳池的蓄水量为380m3 B、该游泳池内开始注水时已经蓄水100m3 C、注水2小时,还需注水100m3 , 可将游泳池注满 D、每小时可注水190m37. 定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1-m,-1-m]的函数的一些结论,其中不正确的是( )A、当m=-3时,函数图象的顶点坐标是( , ) B、当m>0时,函数图象截x轴所得的线段长度大于 C、当m≠0时,函数图象经过同一个点 D、当m<0时,函数在x> 时,y随x的增大而减小8. 如图,在正方形 外取一点 ,连接 , , .过点 作 的垂线交 于点 .若 , .下列结论:
① ;②点 到直线 的距离为 ;③ ;④ ;⑤ .其中正确结论的序号是( )
A、①②③ B、①②④ C、①③⑤ D、②③⑤9. ……依次观察左边三个图形,并判断照此规律从左到右第2019个图形是( ) A、
……依次观察左边三个图形,并判断照此规律从左到右第2019个图形是( ) A、 B、
B、 C、
C、 D、
D、 10. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( )
10. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( ) A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题(每题2分,共16分)
-
11. 小明推铅球,铅球行进高度 与水平距离 之间的关系为 ,则小明推球的成绩是m.12. 平面直角坐标系中点P的坐标为(3,-1),则点P关于x轴的对称点的坐标是.13. 如图,在坐标系中,以坐标原点 O, A (-8,0), B (0,6)为顶点的Rt△AOB ,其两个锐角对应的外角平分线相交于点M,且点M恰好在反比例函数 的图象上,则k的值为.
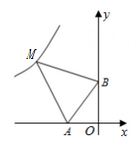 14. 已知:如图,线段 , , , 现点绕着点以的速度逆时针旋转一周后停止,同时点沿直线自点向点运动,若点 , 两点能相遇,则点运动的速度为.
14. 已知:如图,线段 , , , 现点绕着点以的速度逆时针旋转一周后停止,同时点沿直线自点向点运动,若点 , 两点能相遇,则点运动的速度为. 15. 运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识在生活中的应用.16. 若 , , ,则 的大小关系用“<”号排列为 .17. 大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是347,则m的值是 .18. 已知点 为双曲线 上的一点,过点 作 轴、 轴的垂线,分别交直线 于点 、 两点(点 在点 下方.若直线 与 轴交于点 ,与 轴相交于点 ,则 的值为.
15. 运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识在生活中的应用.16. 若 , , ,则 的大小关系用“<”号排列为 .17. 大于1的正整数m的三次幂可“分裂”成若干个连续奇数的和.如23=3+5,33=7+9+11,43=13+15+17+19,…,若m3“分裂”后,其中有一个奇数是347,则m的值是 .18. 已知点 为双曲线 上的一点,过点 作 轴、 轴的垂线,分别交直线 于点 、 两点(点 在点 下方.若直线 与 轴交于点 ,与 轴相交于点 ,则 的值为.三、解答题(共9题,共74分)
-
19. 计算: .20. 先化简,再求值: ,其中 ,21. 请尺规作图完成下列画图,不写画法,保留画图痕迹.
 (1)、如图 1,E在矩形纸片ABCD的边AD上,将纸片折叠,使AB落在CE所在直线上,画出折痕MN(点M,N分别在边AD,BC上);(2)、如图 2,点 A、B、C 均在⊙O 上,且∠BAC=120°,在优弧 BC上画 M、N 两点,使∠MAN=60°.22. 如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且 =
(1)、如图 1,E在矩形纸片ABCD的边AD上,将纸片折叠,使AB落在CE所在直线上,画出折痕MN(点M,N分别在边AD,BC上);(2)、如图 2,点 A、B、C 均在⊙O 上,且∠BAC=120°,在优弧 BC上画 M、N 两点,使∠MAN=60°.22. 如图,AB是⊙O的直径,C是⊙O上一点,OD是半径,且 =求证:AC∥OD
 23. 如图,已知C是线段AB上的一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和正方形CBGF , 点F在CD上,联结AF、BD , BD与FG交于点M , 点N是边AC上的一点,联结EN交AF 与点H .
23. 如图,已知C是线段AB上的一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和正方形CBGF , 点F在CD上,联结AF、BD , BD与FG交于点M , 点N是边AC上的一点,联结EN交AF 与点H .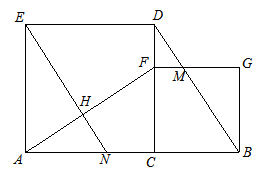 (1)、求证:AF=BD;(2)、如果 ,求证: .24. 新冠肺炎疫情期间,我市防控指挥部想了解自8月1日至8月底各学校教职工介入志愿服务的情况,在全市各学校中随机调查了部分介入志愿者服务的教职工,对他们的志愿服务时间(小时)进行统计,A:0<x≤30;B:30<x≤60;C:60<x≤90;D:90<x≤120;整理并绘制成两幅不完整的统计图,请回答下列问题:
(1)、求证:AF=BD;(2)、如果 ,求证: .24. 新冠肺炎疫情期间,我市防控指挥部想了解自8月1日至8月底各学校教职工介入志愿服务的情况,在全市各学校中随机调查了部分介入志愿者服务的教职工,对他们的志愿服务时间(小时)进行统计,A:0<x≤30;B:30<x≤60;C:60<x≤90;D:90<x≤120;整理并绘制成两幅不完整的统计图,请回答下列问题: (1)、这次被抽取的教职工共有人,扇形统计图中,“D:90<x≤120”所占圆心角的度数是 °;(2)、请你将条形统计图补充完整,并在图上标明相应的数据;(3)、若该市共有3000名教职工参与志愿服务,那么志愿服务时间多于60小时的教职工大约有多少人?25. 已知:在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,点A在点B的左侧,若抛物线的对称轴为x=1,点A的坐标为(−1,0).(1)、求这个二次函数的解析式;(2)、设抛物线的顶点为C,抛物线上一点D的坐标为(−3,12),过点B、 D的直线与抛物线的对称轴交于点E. 问:是否存在这样的点F,使得以点B、C、E、 F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;(3)、在(2)的条件下,若在BD上存在一点P,使得直线AP将四边形ACBD分成了面积相等的两部分,请你求出此时点P的坐标.26. 在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm,求BE的长.”
(1)、这次被抽取的教职工共有人,扇形统计图中,“D:90<x≤120”所占圆心角的度数是 °;(2)、请你将条形统计图补充完整,并在图上标明相应的数据;(3)、若该市共有3000名教职工参与志愿服务,那么志愿服务时间多于60小时的教职工大约有多少人?25. 已知:在平面直角坐标系xOy中,二次函数y=x2+bx+c的图象与x轴交于A、 B两点,点A在点B的左侧,若抛物线的对称轴为x=1,点A的坐标为(−1,0).(1)、求这个二次函数的解析式;(2)、设抛物线的顶点为C,抛物线上一点D的坐标为(−3,12),过点B、 D的直线与抛物线的对称轴交于点E. 问:是否存在这样的点F,使得以点B、C、E、 F为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由;(3)、在(2)的条件下,若在BD上存在一点P,使得直线AP将四边形ACBD分成了面积相等的两部分,请你求出此时点P的坐标.26. 在学习完第十二章后,张老师让同学们独立完成课本56页第9题:“如图1,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=2.5cm,DE=1.7cm,求BE的长.”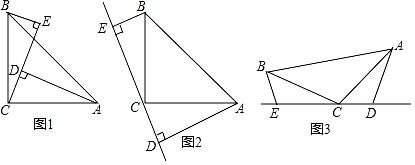 (1)、请你也独立完成这道题;(2)、待同学们完成这道题后,张老师又出示了一道题:在课本原题其它条件不变的前提下,将CE所在直线旋转到△ABC的外部(如图2),请你猜想AD,DE,BE三者之间的数量关系,直接写出结论,不需证明.(3)、如图3,将(1)中的条件改为:在△ABC中,AC=BC,D,C,E三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=α,其中α为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由.27. 数学来源于生活,数学之美无处不在,在几何图形中,最美的角是45°,最美的直角三角形是等腰直角三角形,我们把45°的角称为一中美角,最美的等腰直角三角形称为一中美三角.根据该约定,完成下列问题:
(1)、请你也独立完成这道题;(2)、待同学们完成这道题后,张老师又出示了一道题:在课本原题其它条件不变的前提下,将CE所在直线旋转到△ABC的外部(如图2),请你猜想AD,DE,BE三者之间的数量关系,直接写出结论,不需证明.(3)、如图3,将(1)中的条件改为:在△ABC中,AC=BC,D,C,E三点在同一条直线上,并且有∠BEC=∠ADC=∠BCA=α,其中α为任意钝角,那么(2)中你的猜想是否还成立?若成立,请证明;若不成立,请说明理由.27. 数学来源于生活,数学之美无处不在,在几何图形中,最美的角是45°,最美的直角三角形是等腰直角三角形,我们把45°的角称为一中美角,最美的等腰直角三角形称为一中美三角.根据该约定,完成下列问题: (1)、如图1,已知正方形ABCD中O是对角线AC上一动点,过O作OP⊥OD,垂足为O,交BC边于P,△POD是否为一中美三角,并说明理由;(2)、如图2,在平面直角坐标系中,点A(﹣2,0),点B(0,2),点P在第二象限内,且在直线y=﹣2x﹣2上,若△ABP恰好构成一中美三角,求出此时P点的坐标;(3)、如图3,若二次函数y=﹣x2+2x+3的图象与x轴交于A、B两点,与y轴交于点C,P为第二象限上的点,在直线AC上,且∠OPB恰好构成一中美角;Q为x轴上方抛物线上的一动点,令Q点横坐标为m(0<m<3),当m为何值时,△PBQ的面积最大,求出此时Q点坐标和最大面积.
(1)、如图1,已知正方形ABCD中O是对角线AC上一动点,过O作OP⊥OD,垂足为O,交BC边于P,△POD是否为一中美三角,并说明理由;(2)、如图2,在平面直角坐标系中,点A(﹣2,0),点B(0,2),点P在第二象限内,且在直线y=﹣2x﹣2上,若△ABP恰好构成一中美三角,求出此时P点的坐标;(3)、如图3,若二次函数y=﹣x2+2x+3的图象与x轴交于A、B两点,与y轴交于点C,P为第二象限上的点,在直线AC上,且∠OPB恰好构成一中美角;Q为x轴上方抛物线上的一动点,令Q点横坐标为m(0<m<3),当m为何值时,△PBQ的面积最大,求出此时Q点坐标和最大面积.