云南省2022届高三“3 3 3”高考理数备考诊断性联考试卷（二）

试卷更新日期：2022-05-10 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $M = {x | (x + 1) (x - 3) \leq 0}$ ， $N = {x | \frac{1}{2} < x < 4}$ ，则 $M ∩ N =$ （）

A、 ${x | - 1 \leq x < \frac{1}{2}}$ B、 ${x | \frac{1}{2} < x \leq 3}$ C、 ${x | 3 \leq x < 4}$ D、 ${x | - 1 \leq x < 4}$

查看试题解析
2. $\frac{1 - 2 i}{1 + i} =$ （）

A、 $- \frac{1}{2} - \frac{3}{2} i$ B、 $- \frac{1}{2} + \frac{3}{2} i$ C、 $- \frac{3}{2} - \frac{1}{2} i$ D、 $- \frac{3}{2} + \frac{1}{2} i$

查看试题解析
3. 如图所示的茎叶图记录了甲､乙两种商品连续10天的销售数据，则下列说法错误的是（）

A、乙销售数据的极差为24 B、甲销售数据的众数为93 C、乙销售数据的均值比甲大 D、甲销售数据的中位数为92

查看试题解析
4. 朗伯比尔定律（Lambert-Beerlaw）是分光光度法的基本定律，是描述物质对某一波长光吸收的强弱与吸光物质的浓度及其液层厚度间的关系，其数学表达式为 $A = l g \frac{1}{T} = K b c$ ，其中A为吸光度，T为透光度，K为摩尔吸光系数，c为吸光物质的浓度，单位为 $m o l / L$ ， b为吸收层厚度，单位为 $c m$ .保持K，b不变，当吸光物质的浓度增加为原来的两倍时，透光度由原来的T变为（）

A、2T B、 $T^{2}$ C、 $\frac{1}{2} T$ D、10T

查看试题解析
5. 直线 $y = k x (k > 0)$ 与双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 在第一、第三象限分别交于P、Q两点， $F_{2}$ 是C的右焦点，有 $| P F_{2} | ： | Q F_{2} | = 1 ： \sqrt{3}$ ，且 $P F_{2} ⊥ Q F_{2}$ ，则C的离心率是（）

A、 $\sqrt{3}$ B、 $\sqrt{6}$ C、 $\sqrt{3} + 1$ D、 $\sqrt{6} + 1$

查看试题解析
6. 甲､乙､丙三位同学中只有一人会跳拉丁舞，甲说：我会；乙说：我不会；丙说：甲不会；如果这三人中有且只有一人说真话，由此可判断会跳拉丁舞的是（）

A、甲 B、乙 C、丙 D、无法确定

查看试题解析
7. 如图，在一个正方体中，E，G分别是棱 $A B$ ， $C C^{'}$ 的中点，F为棱 $C D$ 靠近C的四等分点.平面 $E F G$ 截正方体后，其中一个多面体的三视图中，相应的正视图是（）

A、 B、 C、 D、

查看试题解析
8. $\frac{s i n 80 ° + 1}{s i n^{2} 5 ° - 1} =$ （）

A、 $- \frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、-2 D、2

查看试题解析
9. 如图甲，首钢滑雪大跳台是冬奥历史上第一座与工业遗产再利用直接结合的竞赛场馆，大跳台的设计中融入了世界文化遗产敦煌壁画中“飞天”的元素.如图乙，某研究性学习小组为了估算赛道造型最高点A距离地面的高度 $A B$ （ $A B$ 与地面垂直），在赛道一侧找到一座建筑物 $C D$ ，测得 $C D$ 的高度为h，并从C点测得A点的仰角为30°；在赛道与建筑物 $C D$ 之间的地面上的点E处测得A点，C点的仰角分别为75°和30°（其中B，E，D三点共线）.该学习小组利用这些数据估算得 $A B$ 约为60米，则 $C D$ 的高h约为（）米
（参考数据： $\sqrt{2} \approx 1.41$ ， $\sqrt{3} \approx 1.73$ ， $\sqrt{6} = 2.45$ ）

A、11 B、20.8 C、25.4 D、31.8

查看试题解析
10. 随着北京冬残奥会的开幕，吉祥物“雪容融”火遍国内外，现有3个完全相同的“雪容融”，甲､乙､丙3位运动员要与这3个“雪容融”站成一排拍照留念，则有且只有2个“雪容融”相邻的排队方法数为（）

A、36 B、72 C、120 D、432

查看试题解析
11. 已如A，B，C是表面积为 $16 π$ 的球O的球面上的三个点，且 $A C = A B = 1$ ， $∠ A B C = 30 °$ ，则三棱锥 $O - A B C$ 的体积为（）

A、 $\frac{1}{12}$ B、 $\frac{\sqrt{3}}{12}$ C、 $\frac{1}{4}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
12. 定义域为R的函数 $f (x)$ 满足：①对任意 $2 \leq x_{1} < x_{2}$ ，都有 $(x_{1} - x_{2}) [f (x_{1}) - f (x_{2})] > 0$ ；②函数 $y = f (x + 2)$ 的图象关于y轴对称.若实数s，t满足 $f (2 s + 2 t + 2) \leq f (s + 3)$ ，则当 $t \in [0 ， 1]$ 时， $\frac{t + 1}{t + s + 3}$ 的取值范围为（）

A、 $[\frac{1}{4} ， \frac{2}{3}]$ B、 $[\frac{1}{3} ， 2]$ C、 $(- \infty ， \frac{1}{4}] ∪ (\frac{2}{3} ， + \infty)$ D、 $(- \infty ， \frac{1}{3}] ∪ [2 ， + \infty)$

查看试题解析

二、填空题

13. 曲线 $f (x) = \frac{e^{x}}{x - 1}$ 在点 $(0 ， f (0))$ 处的切线方程为.

查看试题解析
14. 若 $| \vec{b} | = 3 | \vec{a} |$ ， $\vec{a} ⊥ (2 \vec{a} - \vec{b})$ ，则 $\vec{a}$ 与 $\vec{b}$ 夹角的余弦值为.

查看试题解析
15. 已知点P在圆 $x^{2} + y^{2} = 1$ 上， $A (- 2 ， 0)$ ， $B (0 ， 2)$ ，则 $\vec{P A} \cdot \vec{P B}$ 的最小值为.

查看试题解析
16. 在锐角三角形 $A B C$ 中，D是线段 $B C$ 上的一点，且满足 $\vec{A B} + \vec{A C} = 2 \vec{A D}$ ， $A D = A B$ ，则 $t a n A + t a n B + t a n C$ 的最小值是.

查看试题解析

三、解答题

17. 冰墩墩是2022年北京冬季奥运会的吉祥物，将熊猫形象与富有超能量的冰晶外壳相结合，头部外壳造型取自冰雪运动头盔，装饰彩色光环，整体形象酷似航天员，深受广大民众的喜爱，已成为最火爆的商品，“一墩难求”.某调查机构随机抽取100人，对是否有意向购买冰墩墩进行调查，结果如下表：
年龄/岁
$[10 ， 20)$
$[20 ， 30)$
$[30 ， 40)$
$[40 ， 50)$
$[50 ， 60)$
$[60 ， 70)$
$[70 ， 80]$
抽取人数
10
20
25
15
18
7
5
有意向购买的人数
10
18
22
9
10
4
2
参考数据： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .
$P (K^{2} \geq k_{0})$
0.15
0.10
0.05
0.025
0.010
0.005
0.001
$k_{0}$
2.072
2.706
3.841
5.024
6.635
7.879
10.828

(1)、若以年龄40岁为分界线，由以上统计数据完成下面的2×2列联表，并判断是否有99.9%的把握认为购买冰墩墩与人的年龄有关？

年龄低于40岁的人数
年龄不低于40岁的人数
总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计

(2)、若从年龄在 $[60 ， 70)$ 的被调查人群中随机选出3人进行调查，设这三人中打算购买冰墩墩的人数为X，求X的分布列和数学期望.

查看试题解析
18. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，满足 $\frac{3}{2 S_{n}} = \frac{1}{a_{n} - 2} - \frac{1}{a_{n} + 4}$ .

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、求数列 ${{(- 1)}^{n} (S_{n} - 3 n)}$ 的前n项和 $T_{n}$ .

查看试题解析
19. 如图，已知直三棱柱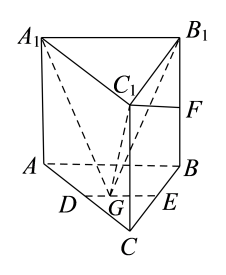 $A_{1} B_{1} C_{1} - A B C$ 中，侧面 $A A_{1} B_{1} B$ 为正方形， $A B = B C = 2$ ， D，E，F分别为 $A C$ ， $B C$ ， $B_{1} B$ 的中点， $C_{1} F ⊥ A_{1} B_{1}$ ， G为线段 $D E$ 上一动点.

(1)、证明： $C_{1} F ⊥ A_{1} G$ ；

(2)、求二面角 $C_{1} - A_{1} G - B_{1}$ 的余弦值的最大值.

查看试题解析
20. 已知圆 $O ： x^{2} + y^{2} = 2$ 与x轴交于A，B两点，动点P满足直线 $A P$ 与直线 $B P$ 的斜率之乘积为 $- \frac{1}{2}$ .

(1)、求动点P的轨迹E的方程；

(2)、过点 $(1 ， 0)$ 的直线l与曲线E交于M，N两点，则在x轴上是否存在定点Q，使得 $\vec{Q M} \cdot \vec{Q N}$ 的值为定值？若存在，求出点Q的坐标和该定值；若不存在，请说明理由.

查看试题解析
21. 已知函数 $f (x) = e^{2 x} + a e^{x} (a \in R)$

(1)、讨论 $f (x)$ 的单调性；

(2)、设 $g (x) = a (1 - x) e^{x} + x^{2}$ ，若方程 $g (x) = f (x)$ 有三个不同的解，求a的取值范围.

查看试题解析
22. 在直角坐标系 $x O y$ 中，以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为 $ρ = 2 c o s θ$ .

(1)、将C的极坐标方程化为直角坐标方程；

(2)、为解决倍立方体问题，数学家引用了蔓叶线.设M为C上的动点，M关于 $x = 1$ 的对称点为N(M、N不与原点重合)，M在x轴的射影为H，直线 $O N$ 与直线MH的交点为P，点P的轨迹就是蔓叶线.请写出P的轨迹的参数方程.

查看试题解析
23. 已知函数： $f (x) = | 2 x + 6 | + | 2 x - 4 | - 11$ ， $g (x) = - | x - 1 |$ .

(1)、请在图中画出 $y = f (x)$ 和 $y = g (x)$ 的图象；

(2)、若 $g (x + t) \leq f (x)$ 恒成立，求t的取值范围.

查看试题解析

年龄/岁	$[10 ， 20)$	$[20 ， 30)$	$[30 ， 40)$	$[40 ， 50)$	$[50 ， 60)$	$[60 ， 70)$	$[70 ， 80]$
抽取人数	10	20	25	15	18	7	5
有意向购买的人数	10	18	22	9	10	4	2

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

	年龄低于40岁的人数	年龄不低于40岁的人数	总计
有意向购买冰墩墩的人数
无意向购买冰墩墩的人数
总计