2022年甘肃省兰州市中考数学模拟试卷三（5月份）

试卷更新日期：2022-05-10 类型：中考模拟

进入出卷网下载

一、单选题（每题3分，共30分）

1. 某校为了了解七年级800名学生期中数学考试情况，从中抽取了100名学生的数学成绩进行了统计，下面判断中正确的有（）
①这种调查的方式是抽样调查；②800名学生的数学成绩是总体；③每名学生的期中数学成绩是个体；④100名学生的数学成绩是总体的一个样本．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 等腰三角形一腰长为5，这一腰上的高为3，则这个等腰三角形底边长为（）

A、 $\sqrt{10}$ B、 $3 \sqrt{10}$ C、 $\sqrt{10}$ 或 $3 \sqrt{10}$ D、 $4$ 或 $3 \sqrt{10}$

查看试题解析
3. 下表记录了一名球员在罚球线上投篮的结果：
投篮次数
50
100
150
200
250
400
500
800
投中次数
28
63
87
122
148
242
301
480
投中频率
0.560
0.630
0.580
0.610
0.592
0.605
0.602
0.600
根据频率的稳定性，估计这名球员投篮一次投中的概率约是（）

A、0.560 B、0.580 C、0.600 D、0.620

查看试题解析
4. 如图所示，在Rt△ABC中，AB=AC，D、E是斜边BC上的两点，且∠DAE=45°，△ADC≌△AFB，连接EF，有下列结论∶①BE=DC；②∠BAF=∠DAC； ③∠FAE=45°；④BF⊥BC．其中正确的有（）

A、①②③④ B、②③ C、②③④ D、③④

查看试题解析
5. 如图，一个条形测力计不挂重物时长5cm，挂上重物后，在弹性限度内弹簧伸长的长度与所挂重物的质量成正比，弹簧总长y（cm）关于所挂物体质量x（kg）的函数图象如图所示，则图中a的值是（　　）

A、15 B、18 C、20 D、33

查看试题解析
6. 如图，点O在 $△ A B C$ 内，且到三边的距离相等，∠A＝64°，则∠BOC的度数为（）

A、58° B、64° C、122° D、124°

查看试题解析
7. 下面结论正确的有（）
① $0$ 是最小的整数；②几个数相乘，积的符号由负因数的个数决定；③ $- 5.32$ 是负分数；④整数和分数统称为有理数；⑤有理数 $a$ 的倒数是 $\frac{1}{a}$ ；⑥有最小的正整数，也有最大的负整数．

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
8. 如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB＝90°，直角边AO在x轴上，且AO＝1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A₁OB₁ ，且A₁O＝2AO，再将Rt△A₁OB₁绕原点O顺时针旋转90°得到等腰三角形A₂OB₂ ，且A₂O＝2A₁O……依此规律，得到等腰直角三角形A_{2 017}OB_{2 017}_.则点B_{2 017}的坐标（）

A、（2^{2 017} ，－2^{2 017}） B、（2^{2 016} ，－2^{2 016}） C、（2^{2 017} ， 2^{2 017}） D、（2^{2 016} ， 2^{2 016}）

查看试题解析
9. 如图，在矩形ABCD 中，AB=4，AD=a，点P在AD上，且AP=2，点E是边AB上的动点，以PE为边作直角∠EPF，射线PF交BC于点F，连接EF，给出下列结论：①tan∠PFE= $\frac{1}{2}$ ；②a的最小值为10.则下列说法正确的是（）

A、①②都对 B、①②都错 C、①对②错 D、①错②对

查看试题解析
10. 对于实数x ，我们规定 $[x]$ 表示不大于x的最大整数，例如 $[1.2] = 1$ ， $[3] = 3$ ，若 $[\frac{x + 4}{10}]$ $= 5$ ，则x的取值可以是（）

A、40 B、45 C、51 D、56

查看试题解析

二、填空题（每题2分，共18分）

11. 若函数 $y = (m - 2) x^{| m | - 1}$ 是正比例函数，则 $m$ 的值是.

查看试题解析
12. 在平面直角坐标系中，已知点P₁(a－1，6)和P₂(3，b－1)关于x轴对称，则(a＋b)²⁰²⁰的值为.

查看试题解析
13. 如图，是由截面为同一种长方形的墙砖粘贴的部分墙面，其中三块横放的墙砖比两块竖放的墙砖低30cm，两块竖放的墙砖比两块横放的墙砖高50cm，则每块墙砖的截面面积是

查看试题解析
14. 对某班同学课外活动最喜欢的项目进行问卷调查（每人选一项），绘制成如图所示的统计图．已知选踢毽子的人数比选打篮球的人数少9入，则选“其他”项目的有人。

查看试题解析
15. 如图，将三角板的直角顶点放在点O处，两条直角边分别交⊙O于A，B，点P在优弧APB上，则∠P的大小为.

查看试题解析
16. 观察下列等式：
${1.4}^{2} - 1^{2} = 3 \times 5$ ；

${2.5}^{2} - 2^{2} = 3 \times 7$ ；

${3.6}^{2} - 3^{2} = 3 \times 9$

${4.7}^{2} - 4^{2} = 3 \times 11$ ；

…………

则第 $n$ （ $n$ 是正整数）个等式为.

查看试题解析
17. 如图，点M是正方形ABCD内一点，△MBC是等边三角形，连接AM、MD对角线BD交CM于点N现有以下结论：
①∠AMD=150°；② $M A^{2} = M N \cdot M C$ ；③ $\frac{S_{△ A D M}}{S_{△ B M C}} = \frac{2 - \sqrt{3}}{3}$ ；④ $\frac{D N}{B N} = \frac{\sqrt{3}}{3}$ ，其中正确的结论有（填写序号）

查看试题解析
18. 在2022年迎新联欢会上，数学老师和同学们做了一个游戏．她在 $A$ ， $B$ ， $C$ 三个盘子里分别放了一些小球，小球数依次为 $a_{0}$ ， $b_{0}$ ， $c_{0}$ ，记为 $G_{0} = (a_{0} ， b_{0} ， c_{0})$ ．游戏规则如下：三个盘子中的小球数 $a_{0} \neq b_{0} \neq c_{0}$ ，则从小球最多的一个盘子中拿出两个，给另外两个盘子各放一个，记为一次操作； $n$ 次操作后的小球数记为 $G_{n} = (a_{n} ， b_{n} ， c_{n})$ ．若 $G_{0} = (3 ， 5 ， 19)$ ，则 $G_{3} =$ ， $G_{2022} =$ ．

查看试题解析

三、解答题（共10题，共72分）

19. 计算： $2 s i n 45 ° \cdot c o s 45 ° + {(\sqrt{2} - 1)}^{0} - \sqrt[3]{- 8}$ ．

查看试题解析
20. 先化简，再求值： $\frac{2 a + 2}{a^{2} - 2 a + 1} \div (2 + \frac{3 - a}{a - 1})$ ，其中 $a = 2$ ．

查看试题解析
21. 如图，在 $10 \times 10$ 的网格图中， $△ A B C$ 的三个顶点都在格点上.

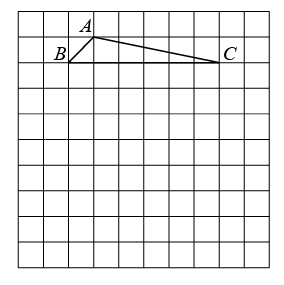
⑴在网格图中画出 $△ A B C$ 的外接圆圆O，并在网格图中标出圆心点O的位置；

⑵在网格图中画出把线段 $A C$ 绕点C按逆时针方向旋转90，得到线段 $C D$ ，并在网格图中标出点D的位置；判断点D是否落在圆O上，若点D落在圆O上，直接写出 $\overset{⌢}{C D}$ 的长.

查看试题解析
22. 据《重庆晨报》，2007年，重庆市被国家评为无偿献血先进城市，医疗临床用血实现了100%来自市民自愿献血，无偿献血总量6.5吨，居全国第三位．现有小莉，小罗，小强三个自愿献血者，两人血型为O型，一人血型为A型．若在三人中随意挑选一人献血，两年以后又从此三人中随意挑选一人献血，试求两次所抽血的血型均为O型的概率．（要求：用列表或画树状图的方法解答）

查看试题解析
23. 操作：第一步：如图1，对折长方形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开.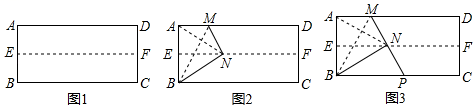
第二步：如图2，再一次折叠纸片，使点A落在EF上的N处，并使折痕经过点B，得到折痕BM，同时得到线段BN.连结AN，易知△ABN的形状是 ▲ .
论证：如图3，若延长MN交BC于点P，试判定△BMP的形状，请说明理由.

查看试题解析
24. “冰墩墩”和“雪容融”分别是北京2022年冬奥会和冬残奥会的吉祥物.2021年十一月初，奥林匹克官方旗舰店上架了“冰墩墩”和“雪容融”这两款毛绒玩具，当月售出了“冰墩墩”200个和“雪容融”100个，销售总额为32000元．十二月售出了“冰墩墩”300个和“雪容融”200个，销售总额为52000元．

(1)、求“冰墩墩”和“雪容融”的销售单价；

(2)、已知“冰墩墩”和“雪容融”的成本分别为90元/个和60元/个．为回馈新老客户，旗舰店决定对“冰墩墩”降价10%后再销售，若一月份销售出这两款毛绒玩具的数量与十二月一样，求该旗舰店当月销售的利润．

查看试题解析
25. 如图所示，Rt△ABC中，已知∠BAC=90°，AB=AC=2，点D在BC上运动（不能到达点B，C），过点D作∠ADE=45°，DE交AC于点E.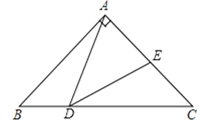

(1)、求证：△ABD∽△DCE；

(2)、当△ADE是等腰三角形时，求AE的长.

查看试题解析
26. 如图，四边形ACDE是证明勾股定理时用到的一个图形，a，b，c是Rt△ABC和Rt△BED边长，易知AE＝ $\sqrt{2}$ c，这时我们把关于x的形如ax²+ $\sqrt{2}$ cx+b＝0的一元二次方程称为“勾系一元二次方程”．
请解决下列问题：

(1)、试判断方程 $x^{2} + 2 x + 1 = 0$ 是否为 “勾系一元二次方程”；

(2)、求证：关于x的“勾系一元二次方程”ax²+ $\sqrt{2}$ cx+b＝0必有实数根；

(3)、若x＝﹣1是“勾系一元二次方程”ax²+ $\sqrt{2}$ cx+b＝0的一个根，且四边形ACDE的周长是12，求△ABC面积．

查看试题解析
27. 如图，直线 $l_{1}$ 的解析式为 $y_{1} = 2 x - 2$ ，它与x轴交于点D．直线 $l_{2} ： y_{2} = k x + b$ 与x轴交于点A，且经过点 $B (3 ， 1)$ ，直线 $l_{1}$ 、 $l_{2}$ 交于点 $C (m ， 2)$ ．

(1)、求点D、点C的坐标；

(2)、求直线 $l_{2}$ 的函数解析式：

(3)、利用函数图象写出关于x、y的二元一次方程组 ${\begin{array}{l} y = 2 x - 2 \\ y = k x + b \end{array}$ 的解．

(4)、求这两条直线与x轴所围成的 $△ A D C$ 的面积．

查看试题解析
28. 如图，抛物线y＝ax²+bx+c与x轴交于点A（﹣3，0）和点B（1，0），与y轴交于点C（0，3）

(1)、求抛物线的解析式并写出其顶点坐标；

(2)、若动点P在第二象限内的抛物线上，动点N在对称轴l上．
①当PA⊥NA，且PA＝NA时，求此时点P的坐标；
②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．

查看试题解析

投篮次数	50	100	150	200	250	400	500	800
投中次数	28	63	87	122	148	242	301	480
投中频率	0.560	0.630	0.580	0.610	0.592	0.605	0.602	0.600