江苏省无锡市锡山区锡东片2022年中考一模数学试卷
试卷更新日期:2022-05-09 类型:中考模拟
一、单选题
-
1. ﹣3的相反数是( )A、﹣3 B、﹣ C、3 D、±32. 下列计算中正确的是( )A、b3•b2=b6 B、x3+x3=x6 C、a2÷a2=0 D、(﹣a3)2=a63. 某自动控制器的芯片,可植入2020000000粒晶体管,这个数字2020000000用科学记数法可表示为A、 B、 C、 D、4. 一条葡萄藤上结有五串葡萄,每串葡萄的粒数如图所示(单位:粒).则这组数据的中位数为( )
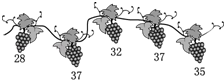 A、32 B、33.8 C、35 D、375. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )
A、32 B、33.8 C、35 D、375. 如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子( )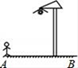 A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长6. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )
A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长6. 如图,直线a∥b,∠1=50°,∠2=30°,则∠3的度数为( )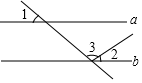 A、40° B、90° C、50° D、100°7. 如图,数轴上点A,B分别对应2,4,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C;以原点O为圆心, 长为半径画弧,交数轴于点M,则点M对应的数是( )
A、40° B、90° C、50° D、100°7. 如图,数轴上点A,B分别对应2,4,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C;以原点O为圆心, 长为半径画弧,交数轴于点M,则点M对应的数是( )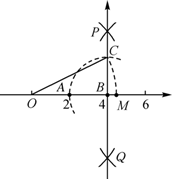 A、 B、 C、5 D、8. 下列图形中阴影部分的面积相等的是( )
A、 B、 C、5 D、8. 下列图形中阴影部分的面积相等的是( )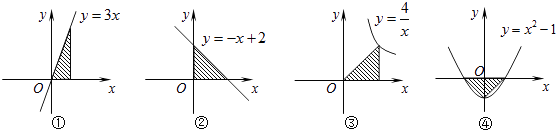 A、②③ B、③④ C、①② D、①④9. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为( )
A、②③ B、③④ C、①② D、①④9. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作为一个圆锥的底面和侧面,则圆锥的表面积为( )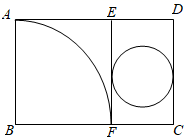 A、 B、 C、 D、10. 如图,已知A,B两点的坐标分别为(8,0),(0,8),点C,F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,sin∠BAD的值是( )
A、 B、 C、 D、10. 如图,已知A,B两点的坐标分别为(8,0),(0,8),点C,F分别是直线x=﹣5和x轴上的动点,CF=10,点D是线段CF的中点,连接AD交y轴于点E,当△ABE面积取得最小值时,sin∠BAD的值是( )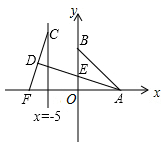 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若在实数范围内有意义,则的取值范围是.12. 方程x(x+1)= x+1的解是.13. 若一个多边形的内角和是900º,则这个多边形是边形.14. 因式分解:2x2y﹣8y3=.15. 如图,点A , B , C在圆O上,∠ACB=54°,则∠ABO的度数是.
 16. 如图, 中, 平分 于点 的延长线交 于点 是 中点,连接 ,若 ,则 的长为.
16. 如图, 中, 平分 于点 的延长线交 于点 是 中点,连接 ,若 ,则 的长为.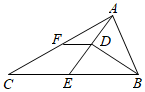 17. 按一定规律排列的一列数: , , , ,……其中第5个数为 , 第n个数为(n为正整数).18. 如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=2 ,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y= (k≠0)的图象恰好过MN的中点,则k的值为 , 点C'的坐标为 .
17. 按一定规律排列的一列数: , , , ,……其中第5个数为 , 第n个数为(n为正整数).18. 如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=2 ,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y= (k≠0)的图象恰好过MN的中点,则k的值为 , 点C'的坐标为 .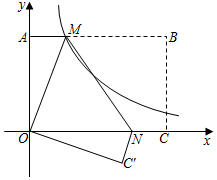
三、解答题
-
19. 计算:(1)、计算: ﹣3tan60°+(π﹣2)0;(2)、解方程组: .20. 图①、图②均是6×6的正方形网格,每个小正方形的顶点称为格点,小正方形边长为1,点A,B,C,D均在格点上.在图①、图②中,只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,不要求写出画法.
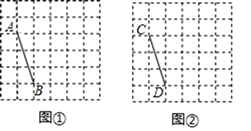 (1)、在图①中以线段AB为边画个中心对称四边形ABEF,使其面积为9;(2)、在图②中以线段CD为边画一个轴对称三角形CDG,使其面积为7.5;21. 如图,已知 AB∥DE, AB=DE,AF=CD,∠CEF=90°
(1)、在图①中以线段AB为边画个中心对称四边形ABEF,使其面积为9;(2)、在图②中以线段CD为边画一个轴对称三角形CDG,使其面积为7.5;21. 如图,已知 AB∥DE, AB=DE,AF=CD,∠CEF=90°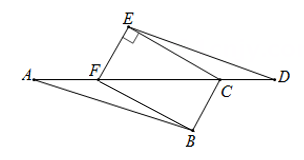
求证:
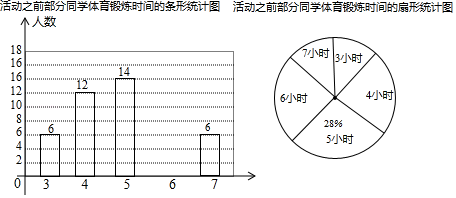
(1)、△ABF≌△DEC;(2)、四边形BCEF是矩形.22. 一个不透明的盒子中放有四张分别写有数字1,2,3,4的红色卡片和三张分别写有数字1,2,3的蓝色卡片,卡片除颜色和数字外完全相同.(1)、从中任意抽取一张卡片,求该卡片上写有数字1的概率;(2)、将3张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成一个两位数,求这个两位数不大于32的概率.23. 重庆一中开展了“爱生活•爱运动”的活动,以鼓励学生积极参与体育锻炼.为了解学生每周体育锻炼时间,学校在活动之前对八年级同学进行了抽样调查,并根据调查结果将学生每周的体育锻炼时间分为3小时、4小时、5小时、6小时、7小时共五种情况.小明根据调查结构制作了如图两幅统计图,请你结合图中所给信息解答下列问题:【整理数据】
“爱生活•爱运动”的活动结束之后,再次抽查这部分学生的体育锻炼时间:
一周体育锻炼时间(小时)
3
4
5
6
7
人数
3
5
15
a
10
活动之后部分学生体育锻炼时间的统计表
【分析数据】
平均数
中位数
众数
活动之前锻炼时间(小时)
5
5
5
活动之后锻炼时间(小时)
5.52
b
c
请根据调查信息分析:
(1)、补全条形统计图,并计算a= , b=小时,c=小时;(2)、小亮同学在活动之前与活动之后的这两次调查中,体育锻炼时间均为5小时,根据体育锻炼时间由多到少进行排名统计,请问他在被调查同学中体育锻炼时间排名靠前的是(填“活动之前”或“活动之后”),理由是;(3)、已知八年级共2200名学生,请估算全年级学生在活动结束后,每周体育锻炼时间至少有6小时的学生人数有多少人?24. 亲爱的同学,你能利用一张矩形纸片折出大小不一的菱形吗?请你动手试一试!然后按要求完成下面问题:
已知某矩形长为8,宽为6,请你用虚线在下图中分别画出两种不同折法的菱形的示意图
并在下方横线上直接写出菱形的面积(画图特别说明: ①示意图中体现所有折痕;②菱形的顶点必须都在矩形的边上 ;③所画菱形是能仅用已知数据便可求出面积的图形)
25. 山地自行车越来越受年轻人的喜爱.某车行经营的A型山地自行车去年销售总额为30万元,今年每辆车售价比去年降低了200元.若卖出的数量相同,销售总额将比去年减少10%,A、B两种型号车的进货和销售价格如表:
A型车
B型车
进货价格(元)
1200
1400
销售价格(元)
今年的销售价格
2200
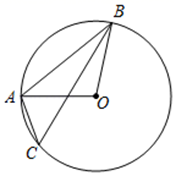
(1)、今年A型车每辆售价多少元?(2)、该车行计划再进一批A型车和新款B型车共60辆,要使这批车获利不少于4万元,A型车至多进多少辆?26. 如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E.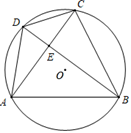 (1)、若∠BAC=40°,则∠ADC=°;∠DAC=°(2)、求证:∠BAC=2∠DAC;(3)、若AB=10,CD=5,求BC的值.27. 如图,抛物线y= x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y= x﹣2经过B、C两点.
(1)、若∠BAC=40°,则∠ADC=°;∠DAC=°(2)、求证:∠BAC=2∠DAC;(3)、若AB=10,CD=5,求BC的值.27. 如图,抛物线y= x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C.直线y= x﹣2经过B、C两点.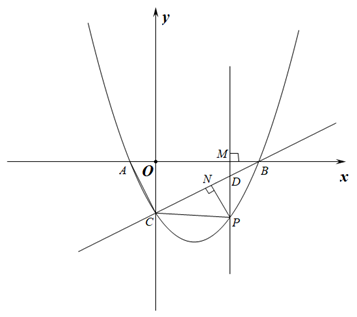
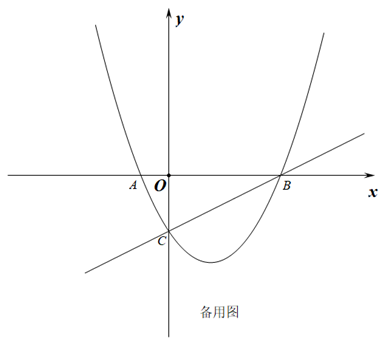 (1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.28. 【学习概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.(1)、【理解运用】
(1)、求抛物线的解析式;(2)、点P是抛物线上的一动点,过点P且垂直于x轴的直线与直线BC及x轴分别交于点D、M.PN⊥BC,垂足为N.设M(m,0).当点P在直线BC下方的抛物线上运动时,是否存在一点P,使△PNC与△AOC相似.若存在,求出点P的坐标;若不存在,请说明理由.28. 【学习概念】有一组对角互余的凸四边形称为对余四边形,连接这两个角的顶点的线段称为对余线.(1)、【理解运用】
如图1,对余四边形中,AB = 5,BC = 6,CD = 4,连接AC,若AC = AB,则cos∠ABC= , sin∠CAD=.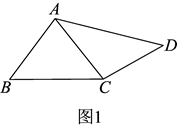 (2)、如图2,凸四边形中,AD = BD,AD⊥BD,当2CD2 + CB2 = CA2时,判断四边形ABCD是否为对余四边形,证明你的结论.
(2)、如图2,凸四边形中,AD = BD,AD⊥BD,当2CD2 + CB2 = CA2时,判断四边形ABCD是否为对余四边形,证明你的结论.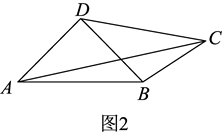 (3)、【拓展提升】
(3)、【拓展提升】
在平面直角坐标中,A(-1,0),B(3,0),C(1,2),四边形ABCD是对余四边形,点E在对余线BD上,且位于△ABC内部,∠AEC = 90° + ∠ABC.设 = u,点D的纵坐标为t,请在下方横线上直接写出u与t的函数表达,并注明t的取值范围 .