江苏省淮安市洪泽实验校2021-2022学年八年级下学期第一次限时作业数学试卷
试卷更新日期：2022-05-09 类型：开学考试
一、单选题
-
1. 下列图形中，中心对称图形是（ ）A、
B、
C、
D、
2. 下列事件中,属于随机事件的是（ ）A、抛掷1个均匀的骰子,出现6点向上 B、在一个仅装着白球和黑球的袋中摸出红球 C、任意三角形的内角和为180° D、13人中至少有2人的生日在同一个月3. 下列调查中，适宜采用普查的是（ ）A、了解我省中学生的视力情况 B、检测一批电灯泡的使用寿命 C、了解我校九（1）班学生校服尺寸情况 D、调查《新闻联播》的收视率4. 中华汉字，源远流长.某校为了传承中华优秀传统文化，组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩，学校随机抽取了其中200名学生的成绩进行统计分析，下列说法正确的是（ ）A、这2000名学生的“汉字听写”大赛成绩的全体是总体 B、每个学生是个体 C、200名学生是总体的一个样本 D、样本容量是20005. 为了记录一个病人的体温变化情况，应选择的统计图是（ ）A、条形统计图 B、扇形统计图 C、折线统计图 D、频数分布直方图6. 下列性质中，平行四边形不一定具备的是（ ）A、对角互补 B、邻角互补 C、对角相等 D、内角和是360°7. 平行四边形的对角线长为x，y，一边长为14，则x，y的值可能是（ ）A、8和16 B、10和14 C、18和10 D、10和248. 如图，点A在平行四边形的对角线上，试判断S1 ， S2之间的大小关系（ ）
A、S1＝S2 B、S1＞S2 C、S1＜S2 D、无法确定二、填空题
-
9. 为估计种子的发芽率，做了10次试验.每次种了1000颗种子，发芽的种子都是950颗左右，预估该种子的发芽率是.10. 在平行四边形ABCD中，若∠B+∠D＝160°，∠C＝°.11. 如图，以正方形ABCD的中心为原点建立平面直角坐标系，点A的坐标为（2，2），则点D的坐标为 .
12. 如图，两个正方形边长分别为2、6，图中阴影部分的面积为.
13. 一组数据分成了五组，其中第三组的频数是10，频率为0.05，则这组数据共有 个数．14. 如图，将△ABC绕点A逆时针旋转50°得到△ADE.若∠E＝65°，且AD⊥BC于点F，则∠BAC的度数为 .
15. 如图，在▱ABCD中， ，在边AD上取点E，使 ，则 等于度.
16. 如图，在平面直角坐标系中，O为原点，四边形OABC是矩形，A（-10，0），C（0，3），点D是OA的中点，点P在BC边上运动，当△ODP是腰长为5的等腰三角形时，点P的坐标是 .
三、解答题
-
17. 一个口袋中有5个黑球和若干个白球，从口袋中随机摸出一球，记下其颜色，再把它放回摇均，重复上述过程，共实验100次，其中75次摸到白球，于是可以估计袋中共有多少球？18. 如图，在▱ABCD中，∠BAD的平分线AE交DC于E，∠DAE＝25°．
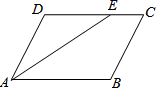(1)、求∠C、∠B的度数；(2)、若BC＝5，AB＝8，求CE的长．19. 央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），请根据图中信息，解答下列问题：
(1)、此次共调查了名学生；(2)、将条形统计图补充完整；(3)、图2中“小说类”所在扇形的圆心角为度；(4)、若该校共有学生2500人，估计该校喜欢“社科类”书籍的学生人数.20. 如图，在平面直角坐标系中，即△ABC的三个顶点分别是A（﹣3，2），B（﹣1，4），C（0，2）.
(1)、将△ABC以点O为旋转中心旋转180°，画出旋转后对应的△A1B1C1.(2)、平移△ABC，若点A的对应点A2的坐标为（﹣5，﹣2）；则点B的对应点坐标是(3)、将△ABC以点O为旋转中心顺时针旋转90°，直接写出点A对应点的坐标(4)、若将△A1B1C1绕某一点旋转可以得到△A2B2C2 ， 请直接写出旋转中心的坐标为.21. 如图，把一张长方形（对边平行）纸条按如图所示折叠.判断三角形HBC的形状，说明理由.
22. 如图，在△ABC中，D是BC边上的中点，F、E分别是AD及其延长线上的点，CF//BE ． 请连接BF、CE ， 试判断四边形BECF是何种特殊四边形，并说明理由．
23. 如图，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE.
(1)、求证：AE＝BC；(2)、若AB＝3，CD＝1，求四边形ABCE的面积.24. 如图，在▱ABCD中，AE⊥BD，CF⊥BD，E，F分别为垂足.
(1)、求证：△ABE≌△CDF.(2)、求证：四边形AECF是平行四边形.25. 如图
(1)、如图1，锐角△ABC中，分别以AB、AC为边向外作等边△ABE和等边△ACD，连接BD，CE，直接写出一对全等三角形：试猜想BD与CE的大小关系，直接写出结论：
(2)、【深入探究】
如图2，△ABC中，∠ABC＝45°，AB＝10cm，BC＝6cm，分别以AB、AC为边向外作正方形ABNE和正方形ACMD，连接BD，求BD的长.(3)、如图3，在（2）的条件下，以AC为直角边在线段AC的左侧作等腰直角△ACD，直接写出BD的长是.26. 探索新知：如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB，∠AOC和∠BOC，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“巧分线”.
(1)、一个角的平分线这个角的“巧分线”；（填“是”或“不是”）(2)、如图2，若∠MPN＝x，且射线PQ是∠MPN的“巧分线”，则∠MPQ＝；（用含x的代数式表示出所有可能的结果）(3)、深入研究：如图2，若∠MPN＝60°，且射线PQ绕点P从PN位置开始，以每秒10°的速度逆时针旋转，当PQ与PN成180°时停止旋转，旋转的时间为t秒.当t为何值时，射线PM是∠QPN的“巧分线”；