湖北省黄石市2021-2022学年九年级下学期3月月考数学试卷
试卷更新日期:2022-05-09 类型:月考试卷
一、选择题
-
1. 有理数﹣ 的倒数为( )A、﹣ B、|﹣ | C、 D、﹣2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、菱形 B、梯形 C、等腰三角形 D、正五边形3. 如图,由8个大小相同的正方体搭成的几何体,从正面看到的形状图是( )
 A、
A、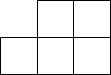 B、
B、 C、
C、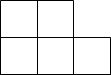 D、
D、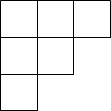 4. 计算(x2)3的结果是( )A、x6 B、x5 C、3x2 D、6x5. 要使式子 有意义,则m的取值范围是( )A、 且 B、 C、 D、6. 已知一组数据:49,50,54,50,55,这组数据的众数是( )A、49 B、50 C、54 D、557. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )
4. 计算(x2)3的结果是( )A、x6 B、x5 C、3x2 D、6x5. 要使式子 有意义,则m的取值范围是( )A、 且 B、 C、 D、6. 已知一组数据:49,50,54,50,55,这组数据的众数是( )A、49 B、50 C、54 D、557. △ABC在平面直角坐标系中的位置如图所示,将其绕点P顺时针旋转得到△A'B'C′,则点P的坐标是( )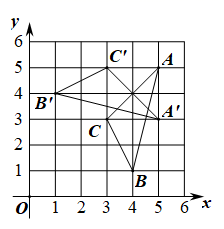 A、(4,5) B、(4,4) C、(3,5) D、(3,4)8. 如图,在以AB为直径的半⊙O中, = ,点D为 上一点,连接OC,BD交于点E,连接OD,若∠DEC=65°,则∠DOC的度数等于( )
A、(4,5) B、(4,4) C、(3,5) D、(3,4)8. 如图,在以AB为直径的半⊙O中, = ,点D为 上一点,连接OC,BD交于点E,连接OD,若∠DEC=65°,则∠DOC的度数等于( ) A、25° B、32.5° C、35° D、40°9. 如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于 GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ).
A、25° B、32.5° C、35° D、40°9. 如图,在△ABC中,AB=AC=6,BC=4,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.以点D为圆心,适当长为半径画弧,交DA于点G,交DC于点H.再分别以点G、H为圆心,大于 GH的长为半径画弧,两弧在∠ADC内部交于点Q,连接DQ并延长与AM交于点F,则DF的长度为( ). A、6 B、 C、 D、810. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,则下列结论中错误的是( )
A、6 B、 C、 D、810. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与y轴交于点B(0,﹣2),点A(﹣1,m)在抛物线上,则下列结论中错误的是( )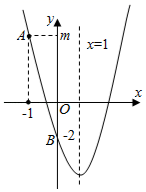 A、ab<0 B、一元二次方程ax2+bx+c=0的正实数根在2和3之间 C、a= D、点P1(t,y1),P2(t+1,y2)在抛物线上,当实数t> 时,y1<y2
A、ab<0 B、一元二次方程ax2+bx+c=0的正实数根在2和3之间 C、a= D、点P1(t,y1),P2(t+1,y2)在抛物线上,当实数t> 时,y1<y2二、填空题
-
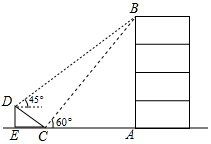
11. 计算: =.12. 因式分解:m3n﹣9mn= .13. ﹣690000000用科学记数法表示 .14. 关于x的方程 =2的解为正数,则a的取值范围为.15. 如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.则大楼AB的高度 .(结果保留根号)
 16. 将一次函数的图象进行上下平移,使得平移之后的图象经过点 , 则平移之后图象的解析式为 .17. 如图,点A,B在反比例函数 的图象上,点C,D在反比例函数 的图象上, 轴,已知点A,B的横坐标分别为2,4, 与 的面积之和为3,则k的值为.
16. 将一次函数的图象进行上下平移,使得平移之后的图象经过点 , 则平移之后图象的解析式为 .17. 如图,点A,B在反比例函数 的图象上,点C,D在反比例函数 的图象上, 轴,已知点A,B的横坐标分别为2,4, 与 的面积之和为3,则k的值为. 18. 如图,正方形ABCD中,点E,F分别为CD,DA延长线上的点,连接EF,BF,BE,BE交AD于点P,过点F作FK⊥BE垂足为G,FK与AB,CD分别交于点H,K,若DC=DE,∠EFB=∠FBC.则下列结论中:①BP=HK;②∠ABF+∠FEB=45°;③PG:GB:PE=1:2:3;④ ;⑤若连接AG,则 ;⑥HF2+HK2=2HB2.结论正确的有 (只填序号).
18. 如图,正方形ABCD中,点E,F分别为CD,DA延长线上的点,连接EF,BF,BE,BE交AD于点P,过点F作FK⊥BE垂足为G,FK与AB,CD分别交于点H,K,若DC=DE,∠EFB=∠FBC.则下列结论中:①BP=HK;②∠ABF+∠FEB=45°;③PG:GB:PE=1:2:3;④ ;⑤若连接AG,则 ;⑥HF2+HK2=2HB2.结论正确的有 (只填序号).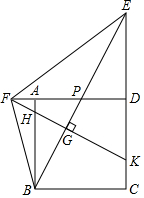
三、解答题
-
19. 先化简,再求值: ,其中x=4.20. 如图,四边形ABCD中,AD BC,E为CD的中点,连结BE并延长交AD的延长线于点F,
 (1)、求证:△BCE≌△FDE;(2)、连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.21. 已知关于x的一元二次方程x2+(2m﹣3)x+m2=0有两个实数根x1 , x2.(1)、求实数m的取值范围;(2)、若x1+x2=6﹣x1x2 , 求m的值.22. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、求证:△BCE≌△FDE;(2)、连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.21. 已知关于x的一元二次方程x2+(2m﹣3)x+m2=0有两个实数根x1 , x2.(1)、求实数m的取值范围;(2)、若x1+x2=6﹣x1x2 , 求m的值.22. 随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: (1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.说明:设“微信,QQ和电话”三种沟通方式分别用字母W,Q和D表示.)23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”
(1)、这次统计共抽查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.说明:设“微信,QQ和电话”三种沟通方式分别用字母W,Q和D表示.)23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”根据以上译文,提出以下两个问题:
(1)、求每头牛、每只羊各值多少两银子?(2)、若某商人准备用19两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?列出所有的可能.24. 如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,D为圆上一点,且B,D两点位于AC异侧,连接BD,交AC于E,点F为BD延长线上一点,连接AF,使得∠DAF=∠ABD.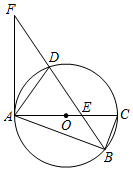 (1)、求证:AF为⊙O的切线;(2)、当点D为EF的中点时,求证:AD2=AO•AE;(3)、在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.25. 已知抛物线与x轴交于A,B两点,且经过点C(0,﹣2),顶点坐标为 .
(1)、求证:AF为⊙O的切线;(2)、当点D为EF的中点时,求证:AD2=AO•AE;(3)、在(2)的条件下,若sin∠BAC= ,AF=2 ,求BF的长.25. 已知抛物线与x轴交于A,B两点,且经过点C(0,﹣2),顶点坐标为 . (1)、求抛物线的解析式;(2)、如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记 的面积为S1 , 的面积为S2 , 当 最大时,求D点坐标;(3)、如图2,连接AC,BC,过点O作直线 ,点P,Q分别为直线l和抛物线上的点.试探究:在y轴右侧是否存在这样的点P,Q,使以点A,B,P,Q为顶点的四边形为平行四边形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,点D为第四象限抛物线上一点,连接AD,BC交于点E,连接BD,记 的面积为S1 , 的面积为S2 , 当 最大时,求D点坐标;(3)、如图2,连接AC,BC,过点O作直线 ,点P,Q分别为直线l和抛物线上的点.试探究:在y轴右侧是否存在这样的点P,Q,使以点A,B,P,Q为顶点的四边形为平行四边形?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.