湖北省黄石市2021-2022学年七年级下学期3月月考数学试卷
试卷更新日期:2022-05-09 类型:月考试卷
一、单选题
-
1. 下面四个图形中,∠1 与∠2是对顶角的图形是( )A、
 B、
B、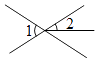 C、
C、 D、
D、 2. 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )
2. 如图,若图形A经过平移与下方图形拼成一个长方形,则正确的平移方式是( )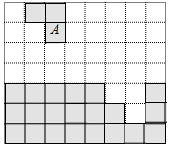 A、向右平移4格,再向下平移4格 B、向右平移6格,再向下平移5格 C、向右平移4格,再向下平移3格 D、向右平移5格,再向下平移3格3. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、
A、向右平移4格,再向下平移4格 B、向右平移6格,再向下平移5格 C、向右平移4格,再向下平移3格 D、向右平移5格,再向下平移3格3. 下列图形中,线段AD的长表示点A到直线BC距离的是( )A、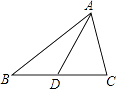 B、
B、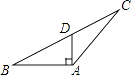 C、
C、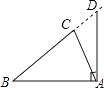 D、
D、 4. 下列命题是假命题的是( )A、对顶角相等 B、两直线平行,内错角相等 C、同角的余角相等 D、两个锐角的和等于直角5. 如图,下列条件中不能判定AB∥CD的是( )
4. 下列命题是假命题的是( )A、对顶角相等 B、两直线平行,内错角相等 C、同角的余角相等 D、两个锐角的和等于直角5. 如图,下列条件中不能判定AB∥CD的是( )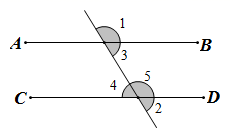 A、∠3=∠5 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠46. 如图.已知.直线分别交于点平分.若.则的度数为( )
A、∠3=∠5 B、∠1=∠5 C、∠1+∠4=180° D、∠3=∠46. 如图.已知.直线分别交于点平分.若.则的度数为( ) A、 B、 C、 D、7. 如图,在宽为20米、长为30米的长方形地面上修筑宽均为2米的道路(图中阴影部分),余下部分种植草坪,则草坪的面积为( )平方米
A、 B、 C、 D、7. 如图,在宽为20米、长为30米的长方形地面上修筑宽均为2米的道路(图中阴影部分),余下部分种植草坪,则草坪的面积为( )平方米 A、500 B、504 C、530 D、5348. 如图所示,a∥b , 则下列式子中值为180°的是( )
A、500 B、504 C、530 D、5348. 如图所示,a∥b , 则下列式子中值为180°的是( ) A、∠α+∠β﹣∠γ B、∠α+∠β+∠γ C、∠β+∠γ﹣∠α D、∠α﹣∠β+∠γ9. 如图,在直角中, , , , , 将沿直线BC向右平移2个单位长度得到 , 连接AD、AE,则下列结论:① , ;②;③四边形ABFD的周长是16;④点D到线段BF的距离是2.4.其中正确的有( )
A、∠α+∠β﹣∠γ B、∠α+∠β+∠γ C、∠β+∠γ﹣∠α D、∠α﹣∠β+∠γ9. 如图,在直角中, , , , , 将沿直线BC向右平移2个单位长度得到 , 连接AD、AE,则下列结论:① , ;②;③四边形ABFD的周长是16;④点D到线段BF的距离是2.4.其中正确的有( ) A、1个 B、2个 C、3个 D、4个10. 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( )
A、1个 B、2个 C、3个 D、4个10. 如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA、CD延长线上的点,∠EAM和∠EDN的平分线交于点F,∠F的度数为( ) A、120° B、135° C、150° D、不能确定
A、120° B、135° C、150° D、不能确定二、填空题
-
11. 如图,为了把河中的水引到 处,可过点 作 于 ,然后沿 开渠,这样做可使所开的渠道最短,这种设计的依据是 .
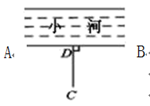 12. 如图,直线 , 且 , , 则.
12. 如图,直线 , 且 , , 则. 13. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转°.
13. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转°.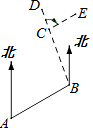 14. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.
14. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.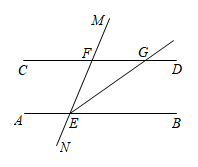 15. 如图,将长方形纸片 沿折痕EF折叠,点 , 的对应点分别为点 , , 交 于点 ,再把三角形 沿 折叠,点 的对应点为点 ,若 ,则 的大小是.
15. 如图,将长方形纸片 沿折痕EF折叠,点 , 的对应点分别为点 , , 交 于点 ,再把三角形 沿 折叠,点 的对应点为点 ,若 ,则 的大小是.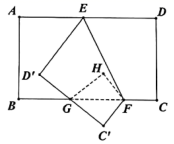 16. 若与的两边分别平行,且比的3倍少24°,则的度数是.
16. 若与的两边分别平行,且比的3倍少24°,则的度数是.三、解答题
-
17. 如图,AB交CD于O,OE⊥AB.
 (1)、若∠EOD=20°,求∠AOC的度数;(2)、若∠AOC:∠BOC=1:2,求∠EOD的度数.18. 如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格.
(1)、若∠EOD=20°,求∠AOC的度数;(2)、若∠AOC:∠BOC=1:2,求∠EOD的度数.18. 如图,在每个小正方形的边长均为1的方格纸中,三角形ABC的顶点都在方格纸的格点上,将三角形ABC先向左平移2格,再向上平移4格. (1)、请在图中画出平移后的三角形A′B′C′;(2)、求出三角形ABC的面积.19. 如图,已知直线MN分别交ED,FC于点A,B,且.
(1)、请在图中画出平移后的三角形A′B′C′;(2)、求出三角形ABC的面积.19. 如图,已知直线MN分别交ED,FC于点A,B,且. (1)、求证:;(2)、若 , , 求的度数.20. 如图,. , CD平分 , .
(1)、求证:;(2)、若 , , 求的度数.20. 如图,. , CD平分 , . (1)、求的度数.(2)、求证:.21. 如图,已知: , , 求证:.完成下面的证明.
(1)、求的度数.(2)、求证:.21. 如图,已知: , , 求证:.完成下面的证明.
证明:∵ , (已知)
, (邻补角定义)
∴ , ( )
∴ , ( )
∴ ( )
∵ , (已知)
∴ , (等量代换)
∴.( )
22. 如图, , . (1)、试判断BF与DE的位置关系,并说明理由;(2)、若 , , 求的度数.23. 如图,已知 , , 射线.
(1)、试判断BF与DE的位置关系,并说明理由;(2)、若 , , 求的度数.23. 如图,已知 , , 射线. (1)、判断射线EF与BD的位置关系,并说明理由;(2)、求 , 的度数.
(1)、判断射线EF与BD的位置关系,并说明理由;(2)、求 , 的度数.

