湖北省黄冈市2021-2022学年七年级下学期第一次测评数学试卷
试卷更新日期:2022-05-09 类型:月考试卷
一、单选题
-
1. 下列四个图形中,不能通过基本图形平移得到的是( )A、
 B、
B、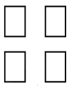 C、
C、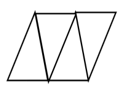 D、
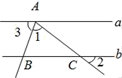
D、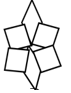 2. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=35°,则∠2等于( )
2. 如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=35°,则∠2等于( ) A、35° B、45° C、55° D、65°3. 下列语句错误的是( )A、连接两点的线段的长度叫做两点间的距离 B、两条直线平行,同旁内角互补 C、若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角 D、平移变换中,各组对应点连成两线段平行(或在同一直线上)且相等4. 某城市有四条直线型主干道分别为l1 , l2 , l3 , l4 , l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.
A、35° B、45° C、55° D、65°3. 下列语句错误的是( )A、连接两点的线段的长度叫做两点间的距离 B、两条直线平行,同旁内角互补 C、若两个角有公共顶点且有一条公共边,和等于平角,则这两个角为邻补角 D、平移变换中,各组对应点连成两线段平行(或在同一直线上)且相等4. 某城市有四条直线型主干道分别为l1 , l2 , l3 , l4 , l3和l4相交,l1和l2相互平行且与l3、l4相交成如图所示的图形,则共可得同旁内角( )对.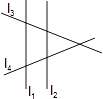 A、4 B、8 C、12 D、165.
A、4 B、8 C、12 D、165.如图,∠AOB=50°,CD∥OB交OA于E,则∠AEC的度数为( )
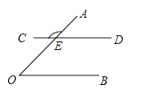 A、120° B、130° C、140° D、150°6. 在同一平面内,有8条互不重合的直线: , , , …, , 若 , , , …,依次类推,则和的位置关系是( )A、平行 B、垂直 C、平行或垂直 D、无法确定7. 如图,将长方形纸片ABCD折叠,使D与B重合,点C落在处,折痕为EF,若∠AEB=70°,则∠的度数是 ( )
A、120° B、130° C、140° D、150°6. 在同一平面内,有8条互不重合的直线: , , , …, , 若 , , , …,依次类推,则和的位置关系是( )A、平行 B、垂直 C、平行或垂直 D、无法确定7. 如图,将长方形纸片ABCD折叠,使D与B重合,点C落在处,折痕为EF,若∠AEB=70°,则∠的度数是 ( )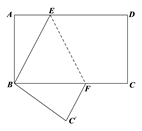 A、125° B、120° C、115° D、110°8. 如图,直线AB∥CD,EG平分∠AEF,EH⊥EG,且平移EH恰好到GF,则下列结论: ①EH平分;②EG=HF;③FH平分;④.其中正确的结论个数是( )
A、125° B、120° C、115° D、110°8. 如图,直线AB∥CD,EG平分∠AEF,EH⊥EG,且平移EH恰好到GF,则下列结论: ①EH平分;②EG=HF;③FH平分;④.其中正确的结论个数是( )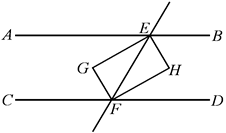 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,已知a∥b,∠1=70°,∠2=40°,则∠3=度.
 10. 如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠DEG=度.
10. 如图,把一张长方形纸片ABCD沿EF折叠,若∠EFG=50°,则∠DEG=度.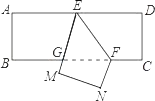 11. 如果两个角的两条边分别平行,且其中一个角比另一个角的4倍少30°,那么这两个角的度数分别为 .12. 如图,为了把河中的水引到 处,可过点 作 于 ,然后沿 开渠,这样做可使所开的渠道最短,这种设计的依据是 .
11. 如果两个角的两条边分别平行,且其中一个角比另一个角的4倍少30°,那么这两个角的度数分别为 .12. 如图,为了把河中的水引到 处,可过点 作 于 ,然后沿 开渠,这样做可使所开的渠道最短,这种设计的依据是 .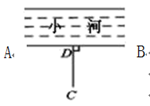 13. 如图,直线 相交于点 为垂足, ,则 度.
13. 如图,直线 相交于点 为垂足, ,则 度.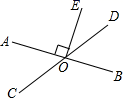 14. 如图, , 点A在直线上, , , 度.
14. 如图, , 点A在直线上, , , 度. 15. 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .
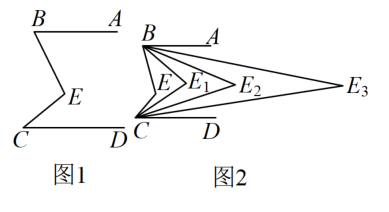
15. 如图,已知AB∥CD,BC∥DE.若∠A=20°,∠C=120°,则∠AED的度数是 .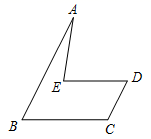 16. 如图,已知 , 、的交点为 , 现作如下操作:
16. 如图,已知 , 、的交点为 , 现作如下操作:第一次操作,分别作和的平分线,交点为 ,
第二次操作,分别作和的平分线,交点为 ,
第三次操作,分别作和的平分线,交点为 ,
…
第次操作,分别作和的平分线,交点为.
若度,那等于度.
三、解答题
-
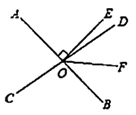
17. 如图,直线 、 相交于 点, 与 的度数比为 , , 平分 ,求 的度数.
 18. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
18. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答.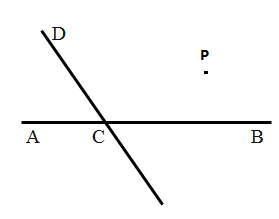 (1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R;(3)、若∠DCB=120°,猜想∠PQC是多少度?并说明理由19. 如图,已知∠ABC+∠ECB=180°,∠P=∠Q,
(1)、过点P作PQ∥CD,交AB于点Q;(2)、过点P作PR⊥CD,垂足为R;(3)、若∠DCB=120°,猜想∠PQC是多少度?并说明理由19. 如图,已知∠ABC+∠ECB=180°,∠P=∠Q, (1)、AB与ED平行吗?为什么?(2)、∠1与∠2是否相等?说说你的理由.20. 完成下列推理过程:
(1)、AB与ED平行吗?为什么?(2)、∠1与∠2是否相等?说说你的理由.20. 完成下列推理过程:如图,已知∠A=∠EDF,∠C=∠F,求证:BC∥EF

证明:∵∠A=∠EDF(已知)
∴ ∥ ( )
∴∠C= ( )
又∵∠C=∠F(已知)
∴ =∠F(等量代换)
∴ ∥ ( )
21. 如图,已知 , . (1)、求证:;(2)、若 , 且 , 求的度数.22. 如图,在△ABC中,∠ACB=90°,AC=8cm,BC=6cm,AB=10cm,点P从点A出发,沿射线AB以2cm/s的速度运动,点Q从点C出发,沿线段CB以1cm/s的速度运动,P、Q两点同时出发,当点Q运动到点B时P、Q停止运动,设Q点的运动时间为t秒.
(1)、求证:;(2)、若 , 且 , 求的度数.22. 如图,在△ABC中,∠ACB=90°,AC=8cm,BC=6cm,AB=10cm,点P从点A出发,沿射线AB以2cm/s的速度运动,点Q从点C出发,沿线段CB以1cm/s的速度运动,P、Q两点同时出发,当点Q运动到点B时P、Q停止运动,设Q点的运动时间为t秒.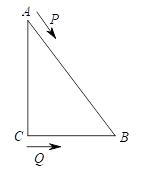 (1)、当t=时,BP=2CQ;(2)、当t=时,BP=BQ;(3)、画CD⊥AB 于点D,并求出CD的值;(4)、当t=时,有S△ACP=2S△ABQ.23. 如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.
(1)、当t=时,BP=2CQ;(2)、当t=时,BP=BQ;(3)、画CD⊥AB 于点D,并求出CD的值;(4)、当t=时,有S△ACP=2S△ABQ.23. 如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.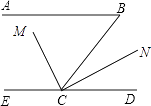 24. 已知:如图, , , 试回答下列问题:
24. 已知:如图, , , 试回答下列问题: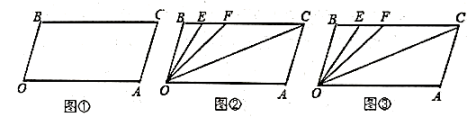 (1)、如图①所示,求证:.(2)、如图②,若点E,F在上,且满足 , 并且平分.
(1)、如图①所示,求证:.(2)、如图②,若点E,F在上,且满足 , 并且平分.(i)求的度数;
(ii)求的值;
(iii)如图③,若.则等于 ▲ .
25. 如图1,已知 , 点A,B分别在 , 上,且 , 射线绕点A顺时针旋转至便立即逆时针回转(速度是a°/秒),射线绕点B顺时针旋转至便立即逆时针回转(速度是b°/秒)、且a、b满足 ,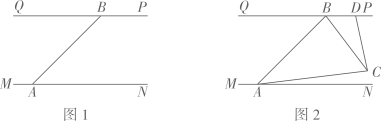 (1)、 , ;(2)、如图2,两条射线同时旋转,设旋转时间为t秒(),两条旋转射线交于点C,过C作交于点D,求与的数量关系;(3)、若射线先旋转20秒,射线才开始旋转,设射线旋转时间为t秒(),若旋转中 , 求t的值.
(1)、 , ;(2)、如图2,两条射线同时旋转,设旋转时间为t秒(),两条旋转射线交于点C,过C作交于点D,求与的数量关系;(3)、若射线先旋转20秒,射线才开始旋转,设射线旋转时间为t秒(),若旋转中 , 求t的值.