湖南省长沙市2021-2022学年九年级下学期3月月考数学试卷
试卷更新日期:2022-05-09 类型:月考试卷
一、单选题
-
1. |-2022|的倒数是( )A、2022 B、 C、-2022 D、-2. 如图所示的工件的主视图是( )
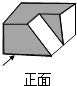 A、
A、 B、
B、 C、
C、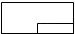 D、
D、 3. 北京冬奥会的开幕式精彩纷呈,吸引了全球人的目光,是收视率最高的一届冬奥会开幕式.据不完全统计,仅中国大陆地区就有大约3.16亿观众收看了北京冬奥会的开幕式,与平昌冬奥会开幕式的全球观看人数相当.将3.16亿用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况5. 在平面直角坐标系中,A( , 2)关于y轴对称的点的坐标为( )A、( , 2) B、(1,) C、( , ) D、(1,2)6. 如图,与位似,点是它们的位似中心,其中 , 则与的面积之比是( )
3. 北京冬奥会的开幕式精彩纷呈,吸引了全球人的目光,是收视率最高的一届冬奥会开幕式.据不完全统计,仅中国大陆地区就有大约3.16亿观众收看了北京冬奥会的开幕式,与平昌冬奥会开幕式的全球观看人数相当.将3.16亿用科学记数法表示为( )A、 B、 C、 D、4. 下列调查中,适合抽样调查的是( ).A、调查本班同学的体育达标情况 B、了解“嫦娥五号”探测器的零部件状况 C、疫情期间,了解全校师生入校时体温情况 D、调查黄河的水质情况5. 在平面直角坐标系中,A( , 2)关于y轴对称的点的坐标为( )A、( , 2) B、(1,) C、( , ) D、(1,2)6. 如图,与位似,点是它们的位似中心,其中 , 则与的面积之比是( ) A、 B、 C、 D、1:97. 如图,矩形ABCD中,对角线AC , BD交于点O , ∠AOD=60°,AD=2,则矩形ABCD的面积是( )
A、 B、 C、 D、1:97. 如图,矩形ABCD中,对角线AC , BD交于点O , ∠AOD=60°,AD=2,则矩形ABCD的面积是( ) A、2 B、 C、 D、88. 的边 经过圆心O, 与圆相切于点A,若 ,则 的大小等于( )
A、2 B、 C、 D、88. 的边 经过圆心O, 与圆相切于点A,若 ,则 的大小等于( ) A、 B、 C、 D、9. 将抛物线y= 向左平移2个单位后,得到的新抛物线的解析式是( )A、 B、y= C、y= D、y=10. 如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2 . 已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是( )
A、 B、 C、 D、9. 将抛物线y= 向左平移2个单位后,得到的新抛物线的解析式是( )A、 B、y= C、y= D、y=10. 如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2 . 已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②;③当0<t≤5时,;④当秒时,△ABE∽△QBP;其中正确的结论是( ) A、①②③ B、②③ C、①③④ D、②④
A、①②③ B、②③ C、①③④ D、②④二、填空题
-
11. 不等式组 的解集是 .12. 分式有意义,则x的取值范围是 .13. 分解因式: .14. 若关于x的一元二次方程ax2+2x﹣1=0无解,则a的取值范围是 .
15. 已知圆锥的底面圆半径为2,其母线长为6,则圆锥的侧面积等于 .16. 如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=6,OB=4,对角线AC、BD交于点G,若曲线y=(x>0)经过点C、G,则k= .
三、解答题
-
17. 计算: .18. 先化简,再求值: , 其中 , .19. 下面是小华设计的“作三角形一边上的高”的尺规作图过程.
已知:△ABC,求作:△ABC的边BC上的高AD.
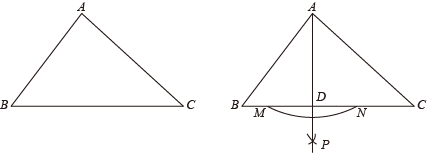
作法:①以点A为圆心,适当长为半径画弧,交直线BC于点M,N;
②分别以点M,N为圆心,以大于的长为半径画弧,两弧相交于点P;
③作直线AP交BC于点D,则线段AD即为所求△ABC的边BC上的高.
试结合小华设计的尺规作图过程,说明AD为什么是△ABC的高.
20. 为积极响应“五项管理”政策,加强学生体育锻炼,某校开设羽毛球、篮球、乒乓球兴趣小组,为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图.请根据两幅统计图中的信息回答下列问题: (1)、求参与调查的学生中,喜爱乒乓球运动的学生人数,并补全条形图;(2)、该校七年级共有660名学生,请你估计该校七年级学生中喜爱篮球运动的学生有多少名?(3)、若从喜爱羽毛球运动的2名男生和2名女生中随机抽取2名学生,确定为该校羽毛球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.21. 如图,已知ABCD,EF为BC边上的垂直平分线, , 且 .
(1)、求参与调查的学生中,喜爱乒乓球运动的学生人数,并补全条形图;(2)、该校七年级共有660名学生,请你估计该校七年级学生中喜爱篮球运动的学生有多少名?(3)、若从喜爱羽毛球运动的2名男生和2名女生中随机抽取2名学生,确定为该校羽毛球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.21. 如图,已知ABCD,EF为BC边上的垂直平分线, , 且 . (1)、求证:;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.22. “燃情冰雪,一起向未来”,北京冬奥会于2022年2月4日如约而至,某商家看准商机,进行冬奥会吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.当销售单价定为46元时,每天可售出400个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个,且规定利润率不得高于50%.设每天销售量为y个,销售单价为x元.(1)、求当每个纪念品的销售单价是多少元时,商家每天获利4800元;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?23. 如图,AB是⊙O的直径,AD平分∠BAC,点C,D在⊙O上,过点D作DE⊥AC,交AC的延长线于点E.
(1)、求证:;(2)、连接AF,请判断四边形ABDF的形状,并说明理由.22. “燃情冰雪,一起向未来”,北京冬奥会于2022年2月4日如约而至,某商家看准商机,进行冬奥会吉祥物“冰墩墩”纪念品的销售,每个纪念品进价40元.当销售单价定为46元时,每天可售出400个,由于销售火爆,商家决定提价销售.经市场调研发现,销售单价每上涨1元,每天销量减少10个,且规定利润率不得高于50%.设每天销售量为y个,销售单价为x元.(1)、求当每个纪念品的销售单价是多少元时,商家每天获利4800元;(2)、将纪念品的销售单价定为多少元时,商家每天销售纪念品获得的利润w元最大?最大利润是多少元?23. 如图,AB是⊙O的直径,AD平分∠BAC,点C,D在⊙O上,过点D作DE⊥AC,交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、若 , , 求AD的长.24. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若 ,则称点D是△ABC中BC边上的“好点”.
(1)、求证:DE是⊙O的切线;(2)、若 , , 求AD的长.24. 定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若 ,则称点D是△ABC中BC边上的“好点”.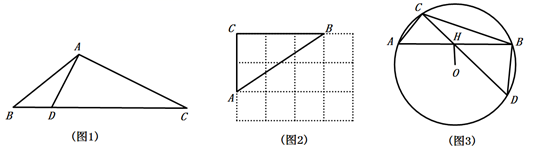 (1)、如图2,△ABC的顶点是 网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)、△ABC中,BC=9, , ,点D是BC边上的“好点”,求线段BD的长.(3)、如图3,△ABC是 的内接三角形,OH⊥AB于点H,连结CH并延长交 于点D.
(1)、如图2,△ABC的顶点是 网格图的格点,请仅用直尺画出AB边上的一个“好点”.(2)、△ABC中,BC=9, , ,点D是BC边上的“好点”,求线段BD的长.(3)、如图3,△ABC是 的内接三角形,OH⊥AB于点H,连结CH并延长交 于点D.①求证:点H是△BCD中CD边上的“好点”.
②若 的半径为9,∠ABD=90°,OH=6,请直接写出 的值.
25. 如图,抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).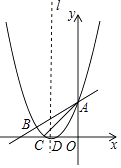 (1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个最大值;(3)、点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于点Q,问:是否存在点P使得以A,P,Q为顶点的三角形与△ABC相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.