新疆昌吉州2022届高三理数第二次诊断性测试试卷

试卷更新日期：2022-05-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知复数 $z$ 满足 $z (1 + i^{3}) = 2 + i$ ，则 $| z | =$ （）

A、 $\sqrt{5}$ B、 $\frac{\sqrt{10}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\sqrt{10}$

查看试题解析
2. 设全集 $U = R$ ，集合 $A = {x | \frac{x - 3}{x + 2} \leq 0}$ ，集合 $B = {x | l n x \geq 1}$ ，则 $A ∩ (∁_{U} B) =$ （）

A、 $(e ， 3)$ B、 $[e ， 3]$ C、 $[- 2 ， e)$ D、 $(- 2 ， e)$

查看试题解析
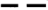3. 《周易》历来被人们视为儒家经典之首，它表现了古代中国人对万事万物的深刻而又朴素的认识，是中华人文文化的基础，它反映了中国古代的二进制计数的思想方法.我们用近代术语解释为：把阳爻“”当做数字“ $1$ ”，把阴爻“”当做数字“ $0$ ”，则八卦代表的数表示如下：
卦名
符号
表示的二进制数
表示的十进制数
坤
000
0
震
001
1
坎
010
2
兑
011
3
…
…
…
…
以此类推，则六十四卦中的符号“”表示的十进制数是（）

A、77 B、155 C、356 D、434

查看试题解析
4. 2022年2月17日—18日，呼图壁县第一届“美丽冰雪，北奥探梦”中小学速滑运动会在昌吉州呼图壁县青少年示范性综合实践基地管理中心举行.为了保障比赛的安全，志愿者小王､小李､小方需要清理 $A$ ､ $B$ ､ $C$ ､ $D$ ､ $E$ ､ $F$ 六条短道速滑跑道，每人至少清理一条跑道，则小王清理三条跑道的情况共有多少种（）

A、120 B、80 C、60 D、40

查看试题解析
5. 已知向量 $| \vec{a} | = 3$ ， $| \vec{b} | = 4$ ，且 $\vec{a} ⊥ \vec{b}$ ， $\vec{c} = λ \vec{a} + (1 - λ) \vec{b} (λ \in R)$ ，则 $| \vec{c} |$ 的最小值为（）

A、 $\frac{6}{5}$ B、 $\frac{12}{5}$ C、 $\frac{36}{5}$ D、 $\frac{48}{5}$

查看试题解析
6. 数列 ${a_{n}}$ 是等差数列， $a_{1} = 1$ ，且 $a_{1} ， a_{2} ， a_{5}$ 构成公比为q的等比数列，则 $q =$ （）

A、1或3 B、0或2 C、3 D、2

查看试题解析
7. 已知函数 $f (x)$ 是定义在 $R$ 上的偶函数，若对于任意 $x_{1} ， x_{2} \in (- \infty ， 0]$ ，不等式 $x_{1} f (x_{1}) + x_{2} f (x_{2}) < x_{1} f (x_{2}) + x_{2} f (x_{1})$ 恒成立，则不等式 $f (1 - x) < f (1)$ 的解集为（）

A、 $(- ∞ ， 0)$ B、 $(0 ， 2)$ C、 $(- \infty ， 0) ∪ (2 ， + \infty)$ D、 $(2 ， + ∞)$

查看试题解析
8. 已知函数 $f (x) = A s i n (ω x + φ) (A > 0 ， ω > 0 ， 0 < φ < \frac{π}{2})$ 的图象过点 $(- \frac{π}{6} ， 0)$ ， $(0 ， \sqrt{3})$ ， $(\frac{π}{3} ， 0)$ ，且 $f (x)$ 在 $[- \frac{π}{6} ， \frac{π}{3}]$ 上仅有1个极值点，则 $f (\frac{π}{4}) =$ （）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、1 D、-1

查看试题解析
9. 已知点 $F_{1}$ ， $F_{2}$ 分别为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左､右焦点，以 $F_{1} F_{2}$ 为直径作圆与双曲线的右支交于点 $P$ ，若 $2 | P F_{1} | - | P F_{2} | = | F_{1} F_{2} |$ ，则双曲线的离心率为（）

A、3 B、4 C、5 D、6

查看试题解析
10. 已知圆 $C_{1} ： {(x - 1)}^{2} + {(y - 1)}^{2} = 1$ ，圆 $C_{2} ： {(x - 4)}^{2} + {(y - 5)}^{2} = 9$ ，点 $M ， N$ 分别是圆 $C_{1}$ ､圆 $C_{2}$ 上的动点，点 $P$ 为 $y = - x$ 上的动点，则 $| P M | + | P N |$ 的最小值是（）

A、4 B、 $\sqrt{61} - 4$ C、 $\sqrt{61} + 4$ D、 $\sqrt{61} + 4$

查看试题解析
11. 在三棱锥 $P - A B C$ 中， $P A = P C = \sqrt{3}$ ，且 $c o s ∠ B A C = \frac{1}{3}$ ， $A B = A C = \sqrt{6}$ ，二面角 $P - A C - B$ 的大小为 $120 °$ ，则三棱锥 $P - A B C$ 的外接球体积为（）

A、 $\frac{5 \sqrt{10}}{3} π$ B、10π C、9π D、 $(4 + 2 \sqrt{3}) π$

查看试题解析
12. 若存在 $\underset{Δ x \to 0}{l i m} \frac{f (x_{0} + Δ x ， y_{0}) - f (x_{0} ， y_{0})}{Δ x}$ ，则称 $\underset{Δ x \to 0}{l i m} \frac{f (x_{0} + Δ x ， y_{0}) - f (x_{0} ， y_{0})}{Δ x}$ 为二元函数 $z = f (x ， y)$ 在点 $(x_{0} ， y_{0})$ 处对 $x$ 的偏导数，记为 ${f^{'}}_{x} (x_{0} ， y_{0})$ ；若存在 $\underset{Δ y \to 0}{l i m} \frac{f (x_{0} ， y_{0} + Δ y) - f (x_{0} ， y_{0})}{Δ y}$ ，则称 $\underset{Δ y \to 0}{l i m} \frac{f (x_{0} ， y_{0} + Δ y) - f (x_{0} ， y_{0})}{Δ y}$ 为二元函数 $z = f (x ， y)$ 在点 $(x_{0} ， y_{0})$ 处对 $y$ 的偏导数，记为 ${f^{'}}_{y} (x_{0} ， y_{0})$ ，已知二元函数 $f (x ， y) = x^{2} - 2 x y + y^{3} (x > 0 ， y > 0)$ ，则下列选项中错误的是（）

A、 ${f^{'}}_{x} (1 ， 3) = - 4$ B、 ${f^{'}}_{y} (1 ， 3) = 10$ C、 ${f^{'}}_{x} (m ， n) + {f^{'}}_{y} (m ， n)$ 的最小值为 $- \frac{1}{3}$ D、 $f (x ， y)$ 的最小值为 $- \frac{4}{27}$

查看试题解析

二、填空题

13. 设 $S_{n}$ 是数列 ${a_{n}}$ 的前 $n$ 项和，且 $S_{n} = 3 a_{n} + 2$ ，则 ${a_{n}}$ 的通项公式为 $a_{n} =$ .

查看试题解析
14. 若实数 $a$ ， $b$ ， $c$ ， $d$ 满足 $l n a = b ， c + 1 = d$ ，则 ${(a - c)}^{2} + {(b - d)}^{2}$ 的最小值为.

查看试题解析
15. 已知点A是焦点为 $F$ 的抛物线 $Γ$ ： $y^{2} = 8 x$ 上的动点，且不与坐标原点 $O$ 重合，线段 $O A$ 的垂直平分线交 $x$ 轴于点 $B$ ．若 $\vec{A C} = \frac{1}{2} \vec{A F}$ ，则 $| A B | - | A C | =$ .

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} 16 x^{2} - 24 x + 9 ， x \leq 1 \\ \frac{1}{9} f (x - 1) ， x > 1 \end{array}$ ，则下列结论正确的有.
① $f (n) = 9^{1 - n}$ ， $n \in N^{*}$
② $\forall x \in (0 ， + \infty)$ ， $f (x) < \frac{1}{x}$ 恒成立
③关于 $x$ 的方程 $f (x) = m (m \in R)$ 有三个不同的实根，则 $\frac{1}{9} < m < 1$
④关于 $x$ 的方程 $f (x) = 9^{1 - n} (n \in N^{*})$ 的所有根之和为 $n^{2} + \frac{n}{3}$

查看试题解析

三、解答题

17. $△ A B C$ 中，角 $A$ ， $B$ ， $C$ 的对边分别是 $a$ ， $b$ ， $c$ ， $(s i n B + s i n C) (b + c) = a s i n A + b s i n C$

(1)、求角 $A$ ；

(2)、若 $D$ 为边 $B C$ 的中点，且 $A D = 1$ ，求 $b c$ 的最大值.

查看试题解析
18. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥$ 平面 $B C C_{1} B_{1}$ ， $A C = 1$ ， $B C = \sqrt{3}$ ， $B B_{1} = 2$ ， $∠ B_{1} B C = 30 °$ .

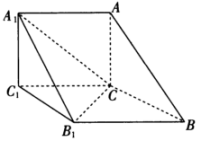(1)、证明： $B_{1} C ⊥$ 平面ABC．

(2)、求二面角 $B_{1} - A_{1} C - C_{1}$ 的余弦值.

查看试题解析
19. 数独是源自18世纪瑞士的一种数学游戏，玩家需要根据 $9 \times 9$ 盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行､每一列､每一个粗线宫（ $3 \times 3$ ）内的数字均含1至9且不重复.数独爱好者小明打算报名参加“丝路杯”全国数独大赛初级组的比赛.
参考数据（其中 $t_{i} = \frac{1}{x_{i}}$ ）
$\sum_{i = 1}^{7} t_{i} y_{i}$
$\bar{t}$
$\sum_{i = 1}^{7} t_{i}^{2} - 7 \times {\bar{t}}^{2}$
1845
0.37
0.55
参考公式：对于一组数据 $(u_{1} ， v_{1})$ ， $(u_{2} ， v_{2})$ ， …， $(u_{n} ， v_{n})$ ，其回归直线 $\hat{v} = \hat{α} + \hat{β} u$ 的斜率和截距的最小二乘估计公式分别为： $\hat{β} = \frac{\sum_{i = 1}^{n} u_{i} v_{i} - n \bar{u} \cdot \bar{v}}{\sum_{i = 1}^{n} u_{i}^{2} - n {\bar{u}}^{2}}$ ， $\hat{α} = \bar{v} - \hat{β} \cdot \bar{u}$ .

(1)、赛前小明在某数独APP上进行一段时间的训练，每天的解题平均速度 $y$ （秒）与训练天数 $x$ （天）有关，经统计得到如表的数据：
$x$ （天）
1
2
3
4
5
6
7
$y$ （秒）
990
990
450
320
300
240
210
现用 $y = a + \frac{b}{x}$ 作为回归方程模型，请利用表中数据，求出该回归方程，并预测小明经过100天训练后，每天解题的平均速度 $y$ 约为多少秒？

(2)、小明和小红在数独APP上玩“对战赛”，每局两人同时开始解一道数独题，先解出题的人获胜，两人约定先胜4局者赢得比赛.若小明每局获胜的概率为 $\frac{2}{3}$ ，已知在前3局中小明胜2局，小红胜1局.若不存在平局，请你估计小明最终赢得比赛的概率.

查看试题解析
20. “工艺折纸”是一种把纸张折成各种不同形状物品的艺术活动，在我国源远流长，某些折纸活动蕴含丰富的数学内容，例如：用一张圆形纸片，按如下步骤折纸（如下图1）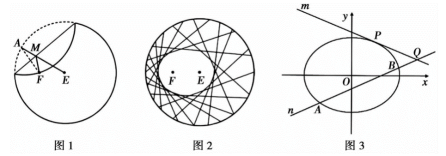
步骤1：设圆心是E，在圆内异于圆心处取一点，标记为F；
步骤2：把纸片折叠，使圆周正好通过点F；
步骤3：把纸片展开，并留下一道折痕；
步骤4：不停重复步骤2和3，就能得到越来越多的折痕（如图2）．
已知这些折痕所围成的图形是一个椭圆．若取半径为4的圆形纸片，设定点F到圆心E的距离为2，按上述方法折纸．

(1)、以点F，E所在的直线为x轴，线段EF的中垂线为y轴，建立坐标系，求折痕所围成的椭圆C（即图1中M点的轨迹）的标准方程．

(2)、如图3，若直线m： $y = - \frac{1}{2} x + s (s > 0)$ 与椭圆C相切于点P，斜率为 $\frac{1}{2}$ 的直线n与椭圆C分别交于点A，B（异于点P），与直线m交于点Q．证明： $| A Q |$ ， $| P Q |$ ， $| B Q |$ 成等比数列．

查看试题解析
21. 对于正实数 $a ， b (a > b)$ ，熟知基本不等式： $G (a ， b) < A (a ， b)$ ，其中 $A (a ， b) = \frac{a + b}{2}$ 为 $a ， b$ 的算术平均数， $G (a ， b) = \sqrt{a b}$ 为 $a ， b$ 的几何平均数．现定义 $a ， b$ 的对数平均数： $L (a ， b) = \frac{a - b}{l n a - l n b} ．$

(1)、设 $x > 1$ ，求证： $l n x < \frac{1}{2} (x - \frac{1}{x})$ ：

(2)、①利用第（1）小问证明不等式： $G (a ， b) < L (a ， b)$ ：
②若不等式 $k \cdot L (a ， b) < G (a ， b) + A (a ， b)$ 对于任意的正实数 $a ， b (a > b)$ 恒成立，求正实数 $k$ 的最大值．

查看试题解析
22. 在极坐标系 $O x$ 中，射线 $l$ 的极坐标方程为 $θ = \frac{π}{3} (ρ \geq 0)$ ，曲线 $C$ 的极坐标方程为 $ρ^{2} - 4 ρ s i n θ = r^{2} - 4 (r > 0)$ ，且射线 $l$ 与曲线 $C$ 有异于点 $O$ 的两个交点 $P$ ， $Q$ .

(1)、求 $r$ 的取值范围；

(2)、求 $\frac{1}{| O P |} + \frac{1}{| O Q |}$ 的取值范围.

查看试题解析
23. 已知函数 $f (x) = | x |$ .

(1)、求不等式 $3 f (x - 1) - f (x + 1) > 2$ 的解集；

(2)、若不等式 $f (x - a) + f (x + 2) \leq f (x + 3)$ 的解集包含 $[- 2 ， - 1]$ ，求 $a$ 的取值范围.

查看试题解析

卦名	符号	表示的二进制数	表示的十进制数
坤		000	0
震		001	1
坎		010	2
兑		011	3
…	…	…	…

$\sum_{i = 1}^{7} t_{i} y_{i}$	$\bar{t}$	$\sum_{i = 1}^{7} t_{i}^{2} - 7 \times {\bar{t}}^{2}$
1845	0.37	0.55

$x$ （天）	1	2	3	4	5	6	7
$y$ （秒）	990	990	450	320	300	240	210