天津市南开区2022届高三下学期一模数学试题

试卷更新日期：2022-05-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | - 2 < x \leq 2}$ ， $B = {x | 1 - x \geq 0}$ ，则 $(∁_{R} A) ∩ B =$ （）

A、 ${x | - 2 \leq x \leq 1}$ B、 ${x | x \leq - 2}$ C、 ${x | 1 \leq x < 2}$ D、 ${x | x > 2}$

查看试题解析
2. 设 $a \in R$ ，则“ $a > 3$ ”是 “ $a^{2} > 4$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 函数 $y = (x^{2} - 1) e^{x}$ 的图象可能是（）

A、 B、 C、 D、

查看试题解析
4. 某区为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照 $[0 ， 0.5)$ ， $[0.5 ， 1)$ ， … $[4 ， 4.5]$ 分成9组，制成了如图所示的频率分布直方图．若该区有40万居民，估计居民中月均用水量在 $[2.5 ， 3)$ 的人数为（）

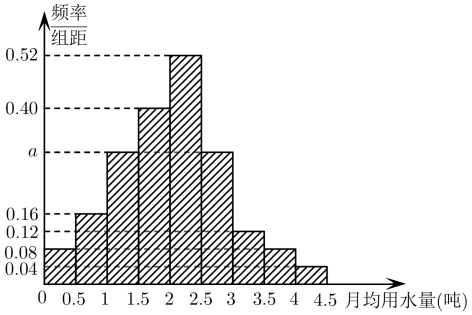A、4.8万 B、6万 C、6.8万 D、12万

查看试题解析
5. 已知直线 $y = m x$ 与圆 $x^{2} + y^{2} - 4 x + 2 = 0$ 相交于A，B两点，若 $| A B | = 2$ ，则m的值为（）

A、 $\pm \sqrt{3}$ B、 $± 1$ C、 $\pm \frac{\sqrt{2}}{2}$ D、 $\pm \frac{\sqrt{3}}{3}$

查看试题解析
6. 已知 $a = {(\frac{1}{2})}^{- 0.6}$ ， $b = l o g_{\frac{1}{2}} \frac{2}{9}$ ， $c = 4^{\frac{1}{3}}$ ，则a，b，c的大小关系是（）

A、 $c < b < a$ B、 $b < a < c$ C、 $a < c < b$ D、 $b < c < a$

查看试题解析
7. 已知双曲线 $\frac{x^{2}}{4} - \frac{y^{2}}{b^{2}} = 1$ 的 $(b > 0)$ 与抛物线 $y^{2} = 4 x$ 的一个交点为M．若抛物线的焦点为F，且 $| F M | = 5$ ，则双曲线的焦点到渐近线的距离为（）

A、 $\sqrt{3}$ B、2 C、 $2 \sqrt{3}$ D、 $\frac{4 \sqrt{3}}{3}$

查看试题解析
8. 将函数 $f (x)$ 的图象向右平移 $\frac{π}{4}$ 个单位长度，得到函数 $g (x) = s i n 2 x$ 的图象，则下列说法错误的是（）

A、函数 $f (x) g (x)$ 是奇函数 B、函数 $f (x) g (x)$ 的图象的一条对称轴方程为 $x = - \frac{π}{8}$ C、函数 $f (x) + g (x)$ 的图象的一个对称中心为 $(\frac{π}{8} ， 0)$ D、函数 $f (x) + g (x)$ 在 $(0 ， π)$ 上单调递减区间是 $[\frac{π}{8} ， \frac{5 π}{8}]$

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} | x + 3 | ， x < 0 ， \\ 2 x^{2} - 6 x + 3 ， x \geq 0 ， \end{array}$ $g (x) = k x + 1$ ．若函数 $h (x) = f (x) - g (x)$ 的图象经过四个象限，则实数k的取值范围是（）

A、 $(- 2 ， \frac{1}{3})$ B、 $(- 10 ， - 2)$ C、 $(- 2 ， + \infty)$ D、 $(- \infty ， - 10) ∪ (\frac{1}{3} ， + \infty)$

查看试题解析

二、填空题

10. 若复数z满足 $(1 - i) z = 6 i$ ，则z的虚部为．

查看试题解析
11. ${(x^{2} - \frac{2}{x})}^{5}$ 的展开式中的 $x$ 项系数为；

查看试题解析
12. 一个三角形的三边长分别为3、4、5，绕最长边旋转一周所得几何体的体积为．

查看试题解析
13. 若 $a > 0$ ， $b > 0$ ， $c > 0$ ， $a + b + c = 2$ ，则 $\frac{4}{a + b} + \frac{a + b}{c}$ 的最小值为．

查看试题解析
14. 某质检员对一批设备的性能进行抽检，第一次检测每台设备合格的概率是0.5，不合格的设备重新调试后进行第二次检测，第二次检测合格的概率是0.8，如果第二次检测仍不合格，则作报废处理．设每台设备是否合格是相互独立的，则每台设备报废的概率为；检测3台设备，则至少2台合格的概率为．

查看试题解析
15. 在△ABC中， $A B = A C = 1$ ， $\vec{A D} = \vec{D B}$ ， $\vec{C D} \cdot \vec{C A} = \frac{1}{A B^{2}}$ ，则 $∠ A B C =$ ；若M是△ABC所在平面上的一点，则 $\vec{M A} \cdot (\vec{M B} + \vec{M C})$ 的最小值为．

查看试题解析

三、解答题

16. 在△ABC中，角A，B，C所对的边分别为a，b，c，且 $a = 3 \sqrt{2}$ ， $b = 6$ ， $C = \frac{3 π}{4}$ ．

(1)、求c；

(2)、求 $c o s (A - \frac{π}{4})$ 的值；

(3)、求 $c o s (A - B - C)$ 的值．

查看试题解析
17. 如图，P，O分别是正四棱柱 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 上、下底面的中心，E是AB的中点， $A A_{1} = 2$ ， $A B = 2 \sqrt{2}$ ．

(1)、求证： $A_{1} E ∥$ 平面PBC；

(2)、求直线PA与平面PBC所成角的正弦值；

(3)、求平面POC与平面PBC夹角的余弦值．

查看试题解析
18. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ $(a > b > 0)$ 的离心率为 $\frac{1}{2}$ ， $F_{1}$ ， $F_{2}$ 是椭圆的两个焦点，P是椭圆上一点，且 $△ P F_{1} F_{2}$ 的周长是6．过点 $M (4 ， 0)$ 的直线l与椭圆C交于点A，B，点B在A，M之间，又线段AB的中点横坐标为 $\frac{4}{7}$ ．

(1)、求椭圆C的标准方程；

(2)、求 $\frac{| A M |}{| M B |}$ 的值．

查看试题解析
19. 已知数列 ${a_{n}}$ 满足 $a_{n + 1} - a_{n} = 1$ ，其前5项和为15；数列 ${b_{n}}$ 是等比数列，且 $b_{1} = 2$ ， $4 b_{2}$ ， $2 b_{3}$ ， $b_{4}$ 成等差数列．

(1)、求 ${a_{n}}$ 和 ${b_{n}}$ 的通项公式；

(2)、设数列 ${b_{n}}$ 的前n项和为 $S_{n}$ ，证明： $S_{n} \cdot S_{n + 2} = S_{n + 1}^{2} - b_{n + 2} (n \in N^{*})$ ；

(3)、比较 $\sum_{i = 1}^{n} a_{i} b_{n + 1 - i}$ 和 $\sum_{i = 1}^{2 n - 1} {(- 1)}^{i - 1} a_{i}^{2}$ 的大小 $(n \in N^{*})$ ．

查看试题解析
20. 设函数 $f (x) = e^{a x} - a l n x (a \in R ， a \neq 0)$ ．

(1)、当 $a = 1$ 时，求曲线 $y = f (x)$ 在点 $(1 ， f (1))$ 处的切线方程；

(2)、若 $f (x)$ 有两个极值点，求a的取值范围；

(3)、当 $a = 1$ 时，若 $0 < b \leq \frac{3 e}{4}$ ，求证： $f (x) + 1 > x^{2} + s i n x + (b x - a) l n x$ ．

查看试题解析