山东省潍坊市2022届高三下学期数学二模试卷

试卷更新日期：2022-05-09 类型：高考模拟

进入出卷网下载

一、单选题

1. 设M，N，U均为非空集合，且满足 $M$ ⫋ $N$ ⫋ $U$ ，则 $(∁_{U} M) ∩ (∁_{U} N) =$ （）

A、M B、N C、 $∁_{u} M$ D、 $∁_{u} N$

查看试题解析
2. 已知直线 $l_{1} ： x - 3 y = 0$ ， $l_{2} ： x + a y - 2 = 0$ ，若 $l_{1} ⊥ l_{2}$ ，则 $a =$ （）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、－3

查看试题解析
3. 已知角 $α$ 的顶点为坐标原点，始边与x轴的非负半轴重合，点 $A (x_{1} ， 2)$ ， $B (x_{2} ， 4)$ 在角 $α$ 的终边上，且 $x_{1} - x_{2} = 1$ ，则 $t a n α =$ （）

A、2 B、 $\frac{1}{2}$ C、-2 D、 $- \frac{1}{2}$

查看试题解析
4. 十七世纪，数学家费马提出猜想：“对任意正整数 $n > 2$ ，关于x，y，z的方程 $x^{n} + y^{n} = z^{n}$ 没有正整数解”，经历三百多年，1995年数学家安德鲁·怀尔斯给出了证明，使它终成费马大定理，则费马大定理的否定为（）

A、对任意正整数n，关于x，y，z的方程 $x^{n} + y^{n} = z^{n}$ 都没有正整数解 B、对任意正整数 $n > 2$ ，关于x，y，z的方程 $x^{n} + y^{n} = z^{n}$ 至少存在一组正整数解 C、存在正整数 $n \leq 2$ ，关于x，y，z的方程 $x^{n} + y^{n} = z^{n}$ 至少存在一组正整数解 D、存在正整数 $n > 2$ ，关于x，y，z的方程 $x^{n} + y^{n} = z^{n}$ 至少存在一组正整数解

查看试题解析
5. 已知函数 $f (x) = l o g_{a} (x - b)$ （ $a > 0$ 且 $a \neq 1$ ）的图像如图所示，则以下说法正确的是（）

A、 $a + b < 0$ B、 $a b < - 1$ C、 $0 < a^{b} < 1$ D、 $l o g_{a} | b | > 0$

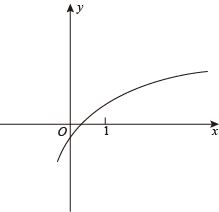查看试题解析
6. 某学校为增进学生体质，拟举办长跑比赛，该学校高一年级共有6个班，现将8个参赛名额分配给这6个班，每班至少1个参赛名额，则不同的分配方法共有（）

A、15种 B、21种 C、30种 D、35种

查看试题解析
7. 已知正实数a，b满足 $a^{2} + 2 a b + 4 b^{2} = 6$ ，则a+2b的最大值为（）

A、 $2 \sqrt{5}$ B、 $2 \sqrt{2}$ C、 $\sqrt{5}$ D、2

查看试题解析
8. 已知函数 $f (x) = l n x - x + t$ ，直线 $l ： y = - \frac{1}{2} x + l n 2 + 2$ ，点 $P (x_{0} ， f (x_{0}))$ 在函数 $y = f (x)$ 图像上，则以下说法正确的是（）

A、若直线l是曲线 $y = f (x)$ 的切线，则 $t = - 3$ B、若直线l与曲线 $y = f (x)$ 无公共点，则 $t > - 3$ C、若 $t = - 2$ ，则点P到直线l的最短距离为 $\sqrt{5}$ D、若 $t = - 2$ ，当点P到直线l的距离最短时， $x_{0} ＝ 2$

查看试题解析

二、多选题

9. 若复数 $z_{1} = 2 + 3 i$ ， $z_{2} = - 1 + i$ ，其中 $i$ 是虚数单位，则下列说法正确的是（）

A、 $\frac{z_{1}}{z_{2}} \in R$ B、 $\bar{z_{1} \cdot z_{2}} = \bar{z_{1}} \cdot \bar{z_{2}}$ C、若 $z_{1} + m (m \in R)$ 是纯虚数，那么 $m = - 2$ D、若 $z_{1} ， \bar{z_{2}}$ 在复平面内对应的向量分别为 $\vec{O A} ， \vec{O B}$ （ $O$ 为坐标原点），则 $| \vec{A B} | = 5$

查看试题解析
10. 已知函数 $f (x) = c o s (2 x + \frac{π}{6})$ 的图象为C，则（）

A、图象C关于直线 $x = \frac{5}{12} π$ 对称 B、图象C关于点 $(\frac{π}{3} ， 0)$ 中心对称 C、将 $y = c o s 2 x$ 的图象向左平移 $\frac{π}{12}$ 个单位长度可以得到图象C D、若把图象C向左平移 $\frac{π}{3}$ 个单位长度，得到函数 $g (x)$ 的图象，则函数 $g (x)$ 是奇函数

查看试题解析
11. 已知四面体ABCD的4个顶点都在球O（O为球心）的球面上，△ABC为等边三角形，M为底面ABC内的动点，AB=BD=2， $A D = \sqrt{2}$ ，且 $A C ⊥ B D$ ，则（）

A、平面ACD⊥平面ABC B、球心O为△ABC的中心 C、直线OM与CD所成的角最小为 $\frac{π}{3}$ D、若动点M到点B的距离与到平面ACD的距离相等，则点M的轨迹为抛物线的一部分

查看试题解析
12. 已知数列 ${a_{n}}$ ， ${b_{n}}$ ，有 $a_{n + 1} = a_{n} - b_{n}$ ， $b_{n + 1} = b_{n} - a_{n}$ ， $n \in N^{*}$ ，则（）

A、若存在 $m > 1$ ， $a_{m} = b_{m}$ ，则 $a_{1} = b_{1}$ B、若 $a_{1} \neq b_{1}$ ，则存在大于2的正整数n，使得 $a_{n} = 0$ C、若 $a_{1} = a$ ， $a_{2} = b$ ，且 $a \neq b$ ，则 $b_{2022} = - b \times 2^{2020}$ D、若 $a_{1} = - 1$ ， $a_{2} = - 3$ ，则关于 $x$ 的方程 $2 a_{3} + (2 a_{3} + 1) c o s x + 2 c o s 2 x + c o s 3 x = 0$ 的所有实数根可构成一个等差数列

查看试题解析

三、填空题

13. 设随机变量X服从标准正态分布 $X ~ N (0 ， 1)$ ，那么对于任意a，记 $Φ (a) = P (X < a)$ ，已知 $Φ (a) = 0.7$ ，则 $P (| X | < a)$ = ．

查看试题解析
14. 若圆 $x^{2} + y^{2} = 1$ 与圆 ${(x - 2)}^{2} + y^{2} = 3$ 的交点为A，B，则 $| A B | =$ ．

查看试题解析
15. 已知定义在 $[0 ， + ∞)$ 上的函数 $f (x)$ 满足 $f (x + 2) = f (x)$ ，且当 $x \in [0 ， 2]$ 时， $f (x) = {\begin{array}{l} \sqrt{3} x ， 0 \leq x \leq 1 ， \\ - \sqrt{3} x + 2 \sqrt{3} ， 1 < x \leq 2 ， \end{array}$ $f (x)$ 图像与x轴的交点从左至右为O， $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， …， $B_{n}$ ， …； $f (x)$ 图像与直线 $y = \sqrt{3}$ 的交点从左至右为 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ， …．若 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ， …， $C_{10}$ 为线段 $A_{8} B_{8}$ 上的10个不同的点，则 $\sum_{i = 1}^{10} (\vec{O A_{2}} \cdot \vec{O C_{i}}) =$ ．

查看试题解析
16. 根据高中的解析几何知识，我们知道平面与圆锥面相交时，根据相交的角度不同，可以是三角形、圆、椭圆、抛物线、双曲线．如图，AB是圆锥底面圆O的直径，圆锥的母线 $P A = 2$ ， $A B = 2 \sqrt{2}$ ， E是其母线PB的中点．若平面 $α$ 过点E，且PB⊥平面 $α$ ，则平面 $α$ 与圆锥侧面的交线是以E为顶点的抛物线的一部分，此时抛物线的焦点F到底面圆心O的距离为；截面 $α$ 把圆锥分割成两部分，在两部分内部，分别在截面 $α$ 的上方作一个半径最大的球M，在截面 $α$ 下方作一个半径最大的球N，则球M与球N的半径的比值为．

查看试题解析

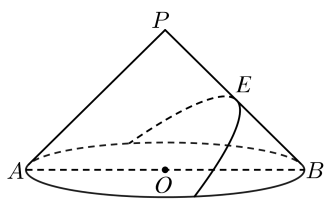
四、解答题

17. 如图，四边形 $A B C D$ 的内角 $B + D = π$ ， $A B = 6$ ， $D A = 2$ ， $B C = C D$ ，且 $A C = 2 \sqrt{7}$ ．

(1)、求 $B$ ；

(2)、若点 $P$ 是线段 $A B$ 上的一点， $P C = 2 \sqrt{3}$ ，求 $P A$ 的值．

查看试题解析
18. 如图，线段AC是圆O的直径，点B是圆O上异于A，C的点， $A C = 2$ ， $B C = 1$ ， PA⊥底面ABC，M是PB上的动点，且 $\vec{P M} = λ \vec{P B} (0 < λ < 1)$ ， N是PC的中点．

(1)、若 $λ = \frac{1}{2}$ 时，记平面AMN与平面ABC的交线为l，试判断直线l与平面PBC的位置关系，并加以证明；

(2)、若平面PBC与平面ABC所成的角为 $\frac{π}{4}$ ，点M到平面PAC的距离是 $\frac{\sqrt{3}}{3}$ ，求 $λ$ 的值．

查看试题解析
19. 已知正项数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{n}^{2} + 2 a_{n} = 4 S_{n}$ ，数列 ${b_{n}}$ 满足 $b_{n} = {(- 2)}^{\frac{a_{n}}{2}}$ ．

(1)、求数列 ${b_{n}}$ 的前n项和 $B_{n}$ ，并证明 $B_{n + 1}$ ， $B_{n}$ ， $B_{n + 2}$ 是等差数列；

(2)、设 $c_{n} = {(- 1)}^{n} a_{n} + b_{n}$ ，求数列 ${c_{n}}$ 的前n项和 $T_{n}$ ．

查看试题解析
20. 已知函数 $f (x) = a x + c o s x + s i n x (a \in R)$ ．

(1)、若 $a = 1$ ，当 $x \in [\frac{π}{2} ， π]$ 时，求证： $f (x)$ 为单调递减函数；

(2)、若 $f (x) \leq 1 + 2 s i n x + 2 c o s x$ 在 $x \in (0 ， π]$ 上恒成立，求实数a的取值范围．

查看试题解析
21. 随着互联网的快速发展和应用，越来越多的人开始选择网上购买产品和服务．某网购平台为提高2022年的销售额，组织网店开展“秒杀”抢购活动，甲，乙，丙三人计划在该购物平台分别参加 $A ， B ， C$ 三家网店各一个订单的“秒杀”抢购，已知三人在 $A ， B ， C$ 三家网店订单“秒杀”成功的概率均为 $p$ ，三人是否抢购成功互不影响．记三人抢购到的订单总数为随机变量 $Z$ ．

(1)、求 $Z$ 的分布列及 $E (Z)$ ；

(2)、已知每个订单由 $k (k \geq 2 ， k \in N^{*})$ 件商品构成，记三人抢购到的商品总数量为 $T$ ，假设 $p = \frac{1}{k} - \frac{k - 1}{2^{k}}$ ，求 $E (T)$ 取最小值时正整数 $k$ 的值．

查看试题解析
22. 已知M，N为椭圆 $C_{1} ： \frac{x^{2}}{a^{2}} + y^{2} = 1 (a > 0)$ 和双曲线 $C_{2} ： \frac{x^{2}}{a^{2}} - y^{2} = 1$ 的公共顶点， $e_{1}$ ， $e_{2}$ 分别为 $C_{1}$ 和 $C_{2}$ 的离心率．

(1)、若 $e_{1} e_{2} = \frac{\sqrt{15}}{4}$ ．
（ⅰ）求 $C_{2}$ 的渐近线方程；
（ⅱ）过点 $G (4 ， 0)$ 的直线l交 $C_{2}$ 的右支于A，B两点，直线MA，MB与直线 $x = 1$ 相交于 $A_{1}$ ， $B_{1}$ 两点，记A，B， $A_{1}$ ， $B_{1}$ 的坐标分别为 $(x_{1} ， y_{1})$ ， $(x_{2} ， y_{2})$ ， $(x_{3} ， y_{3})$ ， $(x_{4} ， y_{4})$ ，求证： $\frac{1}{y_{1}} + \frac{1}{y_{2}} = \frac{1}{y_{3}} + \frac{1}{y_{4}}$ ；

(2)、从 $C_{2}$ 上的动点 $P (x_{0} ， y_{0}) (x_{0} \neq \pm a)$ 引 $C_{1}$ 的两条切线，经过两个切点的直线与 $C_{2}$ 的两条渐近线围成三角形的面积为S，试判断S是否为定值？若是，请求出该定值；若不是，请说明理由．

查看试题解析